Saebin Shin♦ and Wansu Lim°
CRANet-Based Blind Recognition of Channel Coding
Abstract: Blind channel coding recognition is highly useful in non-cooperative communication environments, such as cyber-electronic warfare. Blind channel coding recognition is a technique where the receiver identifies the channel coding scheme without prior knowledge of the coding or any additional data processing. In this paper, we propose CRANet, a network designed to improve channel coding recognition rates in blind environments by utilizing CNN, Residual, and Attention mechanisms. Eight types of channel coding schemes were used: BCH, Hamming, Product, RM, Polar, Golay, Convolutional, and Turbo. Simulation results show that the proposed CRANet outperforms benchmark deep learning models such as TextCNN and CNN-BLSTM, with accuracy improvements of up to 53.5% and 58.7%, respectively. Moreover, when using 2D CNN instead of 1D CNN, the recognition performance improved by 41.36% at –4 dB. Notably, CRANet with 2D CNN achieved an accuracy of 93.62% at 0dB.
Keywords: Channel coding , Blind recognition , Deep learning , Convolution , Residual , Attention
신새빈♦, 임완수°
CRANet을 활용한 블라인드 채널코딩 인식
요 약: 블라인드 채널코딩 인식은 사이버 전자전과 같은 비협력적 통신환경에서 매우 유용하게 사용된다. 블라인드 채널코딩 인식은 인식하고자 하는 채널코딩에 대한 사전지식 및 추가적인 데이터 처리 과정이 없이 수신단에서 채널코딩을 인식하는 기술이다. 본 논문은 블라인드 환경에서 채널코딩 인식률을 높이기 위해 CNN, Residual 그리고 Attention으로 구성한 CRANet을 제안했다. 채널코딩은 BCH, Hamming, Product, RM, Polar, Golay, Convolution, Turbo 등 8가지 유형을 사용했다. 시뮬레이션 결과, 제안한 CRANet의 채널코딩 인식 정확도는TextCNN과 CNN-BLSTM 보다 각각 최대 53.5%와 58,7% 높았다. 또한 CRANet에서 사용한 CNN은 2D를 사용할 때 1D보다 41.36% 더 높은 인식 성능을 보였다. 특히 2D CNN을 사용한 CRANet은 0dB에서 93.62%의 정확도를 달성했다.
키워드: 채널코딩, 블라인드 인식, 딥러닝, 합성곱, 잔차, 어텐션
Ⅰ. 서 론
채널코딩은 에러 탐지와 에러 정정을 통해 무선통신 시스템의 성능을 향상시키는 매우 중요한 통신 기술이 다[1]. 협력적 통신환경에서는 송신부가 사용하는 채널 코딩 유형과 그 파라미터를 수신부가 사전에 알고 있으 므로, 이를 기반으로 신호를 정확하게 디코딩하여 원활 한 통신이 가능하다. 그러나 사이버 전자전, 군사통신 그리고 감청과 같은 비협력적 통신환경에서는 송신부 의 채널 정보가 사전에 수신부로 제공되지 않기 때문에 수신부는 송신부가 사용한 채널코딩 유형을 알 수 없다 [2]. 이로 인해 정확한 디코딩을 할 수 없으며, 수신된 신호가 불완전하거나 왜곡된 형태로 수신될 가능성이 높아진다. 이러한 문제를 해결하기 위해 수신부가 송신 부의 채널코딩 유형과 파라미터를 사전에 알지 못하더 라도 이를 추정할 수 있는 블라인드 채널코딩 인식기술 이 필요하다.
기존 블라인드 채널코딩 인식 연구는 수학적 알고리 즘 혹은 딥러닝을 활용했다. [3]은 확률 기반 채널 추정 기와 소프트 검출기 및 재생기를 통해 채널 상태와 잡음 세기를 추정한 후, average log-likelihood ratio를 사용 하여 Low Density Parity Check(LDPC) 코드의 파라미 터를 인식하는 blind iterative algorithm을 제안했다. [4]는 Reed-Solomon(RS) 코드의 파라미터를 인식하기 위한 channel condition determination 알고리즘을 제안 했다. 이 방법은 채널 상태를 '좋음', '보통', '나쁨'으로 분류하고, 각 조건에 맞는 최적화된 알고리즘을 사용하 여 파라미터를 인식했다. 특히 낮은 SNR 환경에서 lon- gest consecutive zero trust 방식을 도입하여 성능을 향 상시켰다. [5]는 Galos 필드 푸리에 변환과 신뢰성 검증 을 결합한 기법을 사용하여 수신한 코드워드의 스펙트 럼을 계산하고, RS 코드의 파라미터를 인식했다. 하지 만 이러한 수학적 기법들은 블록 코드 또는 특정 코드 유형에만 적용될 수 있다. 또한 특정 코드의 파라미터만 인식할 수 있다는 한계가 있다.
한편 앞서 설명한 수학적 모델링이 아닌 딥러닝을 통한 채널코딩 인식이 활발히 연구되고 있다. [6]은자 연어 처리 기법에서 사용되는 TextCNN을 활용하여 채 널코딩 신호를 텍스트로 변화하여 신호의 패턴을 인식 하는 방법을 제안하였다. 이를 통해 Convolution 코드 의 파라미터를 인식했다. [7]은 Recurrent Neural Network(RNN)과 Attention 매커니즘 그리고 Residual Neural Network(ResNet)을 이용하여 Polar 코드의 파 라미터 인식과 Polar, LDPC, Convolution 그리고 un- ecoded 간의 유형을 인식했다. [8]은 CNN과 Bidirection Long Short Term Memory(BLSTM)을 결 합한 CNN-BLSTM을 통해 LDPC와 5G NR LDPC 유 형 인식과 Convolution 코드 파라미터를 인식했다. 이 러한 딥러닝을 사용한 연구들은 채널코딩 인식 종류의 범위를 늘릴 수 있지만, 더욱 광범위한 채널코딩 인식에 있어서는 제한적이다.
이에, 본 논문은 다양한 채널코딩을 분류하기 위해 Convolution, Residual, 그리고 Attention Network로 구성한 CRANet 딥러닝 모델을 제안한다. CNN은 채널 이 증가하고 레이어가 깊어질수록 기울기 소실 혹은 기 울기 폭주 문제가 발생할 수 있으므로 이러한 문제를 해결하기 위해 Residual[9]을 사용했다. 또한 Attention Mechanism[10]을 활용하여 중요 채널에 가중치를 부여 함으로써 특징 추출 효과를 높였다. Attention은 Channel Attention(CA)과 Spatial Attention(SA)으로 구성했다. 분류하고자 하는 채널코딩 종류는 블록 코드 6개(BCH, Hamming, Product, RM, Polar, Golay)와 비블록 코드(Convolution, Turbo) 2개이다.
일반적으로 신호처리에서 사용되는 데이터는 시계 열성을 갖는 벡터 형태이므로 CNN은 주로 1D CNN[11,12]이 사용된다. 하지만 채널코딩 데이터는 인코 딩 기법에 따라 각기 다른 공간적 특성을 포함한다. 따 라서 본 논문에서는 1D CNN 뿐 아니라 2D CNN을 사용하여, 채널코딩 신호의 복합적인 특성을 더욱 효과 적으로 학습할 수 있도록 한다. 이와 같은 방식은 단순 히 시간적 특성뿐만 아니라 공간적 패턴까지 반영함으 로써, 채널코딩 인식 정확도를 크게 향상시킬 수 있다. 1D CNN을 사용하는 CRANet과 2D CNN을 사용하는 CRANet의 시뮬레이션 결과, 2D CNN을 사용한 CRANet 성능이1D CNN 보다월등히높았다.
또한, 성능평가에서 CRANet은 다양한 채널코딩 유 형을 인식하는 데 있어 타 모델과 비교하였을 때 높은 성능을 보였으며 특히 낮은 SNR에서도 높은 정확도를 보였다. 이는 Residual과 Attention을 결합하여 채널코 딩의 주요 특징을 효과적으로 추출하고 학습할 수 있었 기 때문이다. 특히, 블록 코드와 비블록 코드를 모두 인식하는 능력은 실제 통신환경에서 더욱 중요한 역할 을 할 수 있다.
Ⅱ. CRANet 기반 채널코딩 인식
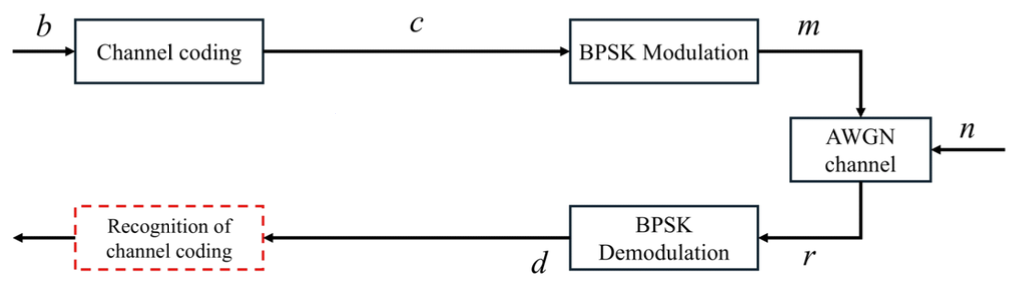
그림 1은 본 논문에서 사용한 시스템 구조이다. b는 채널코딩 전 정보비트이고 랜덤 비트로 생성한다. c는 채널코딩 후 코드워드로 이때 사용한 채널코딩 유형 및 파라미터는 표 1과 같다. 채널코딩 종류는 BCH, Hamming, Product, Reed-Muller(RM), Polar, Golay, Convolution, Turbo 등 총 8가지이고 파라미터는 각각 (15,7), (7,4), (8,4), (11,16), (8,4), (23,12), (2, 1,5), (3,1,4)이다. m은 BPSK로 변조된 신호이다. n은 채널 잡음으로 가산 백색 가우시안 노이즈(additive white gaussian noise, AWGN)를 사용하였다[4,13,14]. 본 논문은 제안한 CRANet이 채널코드 간 구별 및 특징 추출에 집중하고자 비교적 간단한 AWGN 채널을 사용 했다. r은 잡음이 섞인 변조 신호로 r=m+n을 의미한다. d는 복조된 신호로 CRANet을 통한 채널코딩 인식을 위해 사용한다
표 1.
| Coding types | Parameters |
|---|---|
| BCH | (15, 7) |
| Hamming | (8, 4) |
| Product | (8, 4) |
| Reed-Muller(RM) | (16, 11) |
| Polar | (8, 4) |
| Golay | (23, 12) |
| Convolution | (2, 1, 5) |
| Turbo | (3, 1, 4) |
2.1 CRANet 딥러닝 모델
CRANet은 CNN, Residual, Attention으로 이루어진 딥러닝 네트워크이다. CNN은 각 채널코딩의 인코딩 알고리즘 특징을 파악하는 역할을 한다. 그러나 CNN 구조만으로는 채널코딩의 특징을 추출하는 데 한계가 있다. 이때 CNN을 보조하고 성능을 향상하기 위해 Residual과 Attention을 추가했다. Residual은 학습 중 에 발생할 수 있는 기울기 소실 또는 기울기 폭주를 막기 위해 사용하며, Attention은 특징맵의 더 중요한 부분을 강조하여 CNN의 특징 추출 효과를 향상하기 위해 사용한다.
2.1.1 Residual
딥러닝은 레이어 수가 많아질 때, 레이어가 적은 구 조보다 성능이 낮아지는 경우가 발생한다. 이는 딥러닝 학습 과정 중 레이어가 깊어지면서 기울기 소실 또는 기울기 폭주가 발생하기 때문이다. 이에 따라 학습이 원활히 이루어지지 않고 오히려 성능이 저하되는 결과 를 초래한다. Residual은 딥러닝 학습 과정에서 발생하 는 기울기 소실 또는 기울기 폭주를 막음으로써 과적합 을 방지할 수 있는 딥러닝 구조이다[9]. 그림 2는 re- sidual 연결을 나타낸다. 입력값 X는 레이어를 거쳐 F(X)를 생성한다. F(X)는 처음 입력값 X와 더해져 [TeX:] $$\begin{equation} H(X)=F(X)+X \end{equation}$$을 생성하고, H(X)는 다음 레이어의 입력 이 된다. 이처럼 Residual은 레이어의 입력값과 출력값 을 더해줌으로써 학습 난이도를 낮추는 효과를 얻는다.
2.1.2 Attention Mechanism
Attention 구조는 딥러닝 네트워크가 입력 데이터 내 에서 중요한 정보에 집중할 수 있도록 하는 기법이다. 일반적인 CNN은 전체 입력 데이터의 모든 영역에 대 해 특징을 추출한다. 하지만 실제 데이터는 모 든 영역이 동일한 중요도를 가지지 않기 때문에, CNN은 최적의 성능을 발휘하기 어렵다. 특히 채널코딩 인식을 위해 사용하는 데이터는 채널 잡음이 섞인 신호이므로 입력 데이터의 모든 부분이 유효한 데이터라고 할 수 없다. 또한 채널코딩은 인코딩 방식에 따른 특정 패턴이나 위 치가 다른 정보보다 더 중요하다. 이러한 채널코딩 특징 을 고려할 때 Attention 기법을 사용함으로써 딥러닝 네트워크가 중요한 정보에 집중하여 더욱 정교하고 효 율적인 특징 추출을 할 수 있도록 돕는다. 본 논문에서 사용하는 Attention 기법은 Convolutional Block Attention Module[10](CBAM) 구조로 Channel Attention과 Spatial Attention으로 구성한다. CBAM은 입력 특징맵에 대한 채널과 공간의 두 가지 차원에서 주의를 기울이며, 이를 통해 중요한 정보를 강조한다.
1) Channel Attention
Channel Attention은 입력 특징맵의 전체 채널에 대 해 각 채널이 가지는 중요도를 학습한다. 이를 통해 특 정 채널에 더욱 집중하여, 중요한 특징을 더욱 명확히 추출할 수 있다. 그림 3은 CA 구조이다. 입력 특징맵 F의 모든 채널에 글로벌 평균 풀링(Global Average Pooling, GAP)과 글로벌 최대 풀링(Global Max Pooling, GMP)을 각각 적용하여 풀링 벡터 Fc.avg 와 Fc.max 를 생성한다. 이때 각 채널 해상도 H x W 의 크기 는 1이 되고 입력 특징맵의 채널 수 C는 풀링 벡터의 길이가 된다. 이는 각 채널이 전체 특징맵에서 가지는 평균 및 최대 특성을 반영한다. 그다음 벡터는 동일한 멀티레이어 퍼셉트론(Shared MLP)을 거친다. 이때 MLP는 하나의 은닉층을 가지며 r의 감소 비율로 압축 되고 출력층에 의해 원래 길이로 돌아온다. 즉 은닉층의 길이는 C/r을 가진다. Shared MLP를 거쳐 활성화된 두 풀링 벡터는 요소별 합으로 더해져 하나의 벡터를 형성한다. 이 하나의 벡터는 시그모이드 함수를 통해 활성화되어 CA 벡터 Mc가 생성된다. CA를 수식으로 나타내면식(1)같다.
이때 [TeX:] $$\begin{equation} \sigma \end{equation}$$는 시그모이드 함수이다. 이렇게 구해진 CA 벡 터 Mc(F)는 입력 특징맵 F와 곱해져 각 채널에 가중치 를 부여한다. 식(2)는 CA가 적용된 특징맵 Fc를 나타낸 다.
2) Spatial Attention
Spatial Atention은 입력 특징맵의 공간적 위치 정보 를 강조하여 학습중 중요한 공간적 특징에 집중할 수 있도록 돕는다. CA가 특징맵의 각 채널 간의 중요도를 학습하는 반면, SA는 특징맵의 공간적 차원에서 중요 한 위치를 강조하는 역할을 한다. 다시 말해 SA는 채널 의 어느 위치가 중요한지 파악하도록 학습한다. 그림 4는 SA의 구조이다. 처음 입력 특징맵 F는 채널 축 방 향을 따라 GAP와 GMP를 적용하여 풀링맵 Fs.avg와 Fs.max를 각각 생성한다. 즉 CxHxW 차원을 가지는 입력 특징맵은 1xHxW 차원을 가지는 풀링맵이 된다. 이러한 풀링맵은 각 위치에 대한 전역적 정보를 유지하면서, 공간적 특징을 학습하는데 기여한다. 이후 두개의 풀링맵은 직렬 결합(1)으로 2xHxW 차원을 가지는 하나의 특징맵을 형성한다. 이때의 특징맵은 Conv layer를 통해 1개의 채널(2)이 되고, 이후 시그모이 드 함수로 활성화하여 SA 채널 Ms를 생성한다. SA를 수식으로 나타내면 식(3)과 같다.
이때 f는 2개의 채널을 1개의 채널로 줄이기 위한 conv layer이고, GAP와 GMP는 채널 축 방향 풀링을 의미한 다. “;”는 두 특징맵의 직렬 결합을 의미한다. 이렇게 구해진 SA 채널 Ms는 입력 특징맵 F와 곱해져 공간적 으로 중요한 정보를 강조한다. 식(4)는 SA가 적용된 특 징맵 Fs를 나타낸다.
이러한 CA과 SA의 조합은 CRANet이 입력 데이터의 중요 특징을 효과적으로 학습하게 함으로써, 채널코딩 유형 분류 성능을 크게 향상시킨다. 또한 2개의 Attention 메커니즘은 특징맵의 중요 채널과 공간적 위 치를 자동으로 강조하여, 더욱 정확하고 효과적인 예측 을 가능하게 한다.
Ⅲ. 시뮬레이션 및 성능평가
3.1 실험 환경
CRANet 학습을 위한 데이터는 그림 1에서 설명한 바와 같이 인코딩된 랜덤 비트가 BPSK 변조, AWGN 채널 그리고 BPSK 복조를 거친 신호를 사용한다. Turbo 코드를 제외한 7가지 채널코딩은 Python으로 생 성하고, Turbo는 Matlab으로 생성했다. 신호 대 잡음비 (Signal to Noise Ratio, SNR)는 -10dB부터 10dB까지 1dB 간격으로 적용했다. 입력 데이터의 차원은 2D의 경우 (1x128x128)이고 1D의 경우 (1x512)이다. 데이 터 수는 각 채널코딩의 1dB마다 1,000개씩 생성했고, 7:2:1의 비율로 학습, 검증 그리고 시험용으로 분리했 다. 표 4는 학습을 위한 하이퍼파라미터이다.
표 2.
| Layer name | Output size | Parameters | |||
|---|---|---|---|---|---|
| Conv1 | 32 x 64 x 64 | Filter 3x3 Stride 2 Padding 1 | |||
| CRA Module1_1 | 32 x 64 x 64 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| CRA Module1_2 | 32 x 64 x 64 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| Conv2 | 64 x 32 x 32 | [TeX:] $$\begin{equation} [3 \times 3,2,1] \end{equation}$$ | |||
| CRA Module2_1 | 64 x 32 x 32 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| CRA Module2_2 | 64 x 32 x 32 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| Conv3 | 128 x 16 x 16 | [TeX:] $$\begin{equation} [3 \times 3,2,1] \end{equation}$$ | |||
| CRA Module3_1 | 128 x 16 x 16 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| CRA Module3_2 | 128 x 16 x 16 | [TeX:] $$\begin{equation} \left[\begin{array}{l} 3 \times 3,1,1 \\ 3 \times 3,1,1 \end{array}\right] \end{equation}$$ | |||
| GlobalAvgPool | 128 x 1 x 1 | - | |||
| FC | 8 x 1 | - | Channel Attention | - | r = 16 |
| Spatial Attention | - | [TeX:] $$\begin{equation} [7 \times 7,1,1] \end{equation}$$ |
이때 Dropout은 CNN 적용 전에 사용하며, BatchNormalize는 CNN 적용 후에 적용한다. Scheduler는 학습 간 학습률 조절을 위해 적용한다. 초 기 최대 학습률은 0.1, 주기는 20 epoch, 주기당 최대 학습률 감소율은 0.5로 설정한다. Epoch는 100으로 설 정하고, early stopping 횟수는 5회로 설정한다, 이와 같은 기법들은 학습 중의 과적합을 방지하며 더욱 효과 적인 학습을 가능하게 한다. 활성화 함수는 음수 입력에 대해 작은 기울기를 유지해 뉴런 의 학습을 지 속 해서 도 와주기 위해 ReLU가 아닌 LeakyReLU를 사용하였다. 특히, 표 5에서 알 수 있 듯이 활성화 함수로 ReLU보다 LeakyReLU를 사용하였을 때, 더 높은 성능을 달성하 여 LeakyReLU를 사용한다.
표 3.
| Layer name | Output size | Parameters |
|---|---|---|
| CRA Module1 | 32 x 256 | Filter 2 Stride 2 |
| CRA Module2 | 64 x 128 | [TeX:] $$\begin{equation} [1 \times 2,2] \end{equation}$$ |
| CRA Module3 | 128 x 64 | [TeX:] $$\begin{equation} [1 \times 2,2] \end{equation}$$ |
| CRA Module4 | 256 x 32 | [TeX:] $$\begin{equation} [1 \times 2,2] \end{equation}$$ |
| CRA Module5 | 512 x 16 | [TeX:] $$\begin{equation} [1 \times 2,2] \end{equation}$$ |
| GlobalAvgPool | 128 x 1 | - |
| FC | 8 x 1 | - |
| Channel Attention | - | r = 16 |
| Spatial Attention | - | [TeX:] $$\begin{equation} [1 \times 3,1,1] \end{equation}$$ |
표 4.
| Hyperparameter | setting |
|---|---|
| Activation | LeakyReLU |
| Optimizer | Adam |
| Scheduler | CosineAnnealingWarmUpRestarts |
| Dropout | 0.25 |
| BatchNormalize | - |
| Batch size | 300 |
| Epoch | 100 |
| Early stopping | 5 |
3.2 실험결과
그림 6은 CRANet2D, CRANet1D와 벤치마크 모델인 TextCNN[6], CNN-BLSTM[8]의 채널코딩 디코딩 전, 전체 채널코딩 인식 비교 그래프이다. 모든 SNR 영역 에서 CRANet은 벤치마크 모델보다 높은 성능을 보였 다. 동일한1D CNN 구조를 사용하는 CRANet1D와 TextCNN을 비교했을 때, CRANet1D는 3dB 성능 이득 을 보였다. 이는 채널코딩의 경우 시퀸스 신호처리를 텍스트 처리로 바꾸는 것보다 원본 데이터를 사용하는 것이 채널코딩의 특징을 더욱 잘 파악할 수 있기 때문이 다. 한편, LSTM을 사용한 CNN-BLSTM 모델은 가장 낮은 성능을 보였는데, 이는 다양한 채널코딩 유형 인식 에 있어 시계열 데이터 처리 방식인 LSTM이 상대적으 로 불리하게 작용했음을 의미한다. CRANet2D는 CRANet1D에 비해 약 4dB의 성능 이득을 보였다. 특히 0dB에서 CRANet2D는 93.62%, CRANet1D은 69.22% 를 기록하였다. 또한 CRANet2D는 음의 SNR 영역인 -5dB에서도 60.35%의 정확도를 유지하며 타 모델 대 비 우수한 인식 성능을 보였다. CRANet2D는 1dB 이상 부터 약 96%의 정확도를 기록하며, 높은 SNR에서도 매우 효과적이고 우수한 채널코딩 인식 모델임을 입증 한다.
그림 7은 CRANet2D의 SNR에 따른 혼동행렬을 나 타낸다. 가로축은 실제값, 세로축은 예측값을 의미하며, 각 셀의 수치는 정확도 백분율(%)을 의미한다. 그림 7(a)는 10dB의 결과로, Golay 코드를 제외한 BCH, Hamming, Product, RM, Polar, Convolution, Turbo는 100%의 정확도를 달성했다. 반면, Golay 코드는 73% 로 비교적 낮은 정확도를 보였으며, 특히 Turbo 코드에 대해 12%의 오차를 보였다. 그림 7(b)는 0dB의 결과로, BCH, RM 그리고 Golay 코드를 제외한 5가지 코드에 대해서 100% 정확도를 보였으며, BCH 코드도 99.2% 로 매우 높은 정확도를 기록했다. 그러나 RM과 Golay 코드는 각각 78.4%와 71.4%의 정확도를 가진다. RM 코드는 Golay 코드에 대해 11.8%로 오차를 나타냈고, Golay 코드는 10dB 때와 유사하게 Turbo 코드에 대해 12.6%의 오차를 보였다. 그림 7(c)는 –3dB의 결과로, Hamming, Product, Polar, Convolution 그리고 Turbo 코드는 97% 이상의 정확도를 기록했다. 반면 BCH와 RM 코드는 Golay 코드에 대해 각각 60.7%와 69.5%의 오차를 보였다. Golay 코드는 이전 10dB와 0dB일 때와 유사하게 다른 코드들에 대해 비슷한 오차를 보였다. Golay 코드가 높은 SNR에서와는 반대로 BCH와 RM 코드보다 더 높고 일정한 정확도를 가지는 이유는 코드 워드 길이와 인코딩 시 생성되는 높은 중복성 및 독특한 패턴 때문이다. Golay 코드의 코드워드는 23비트로 논 문에서 사용한 채널코드 중 가장 길다. 긴 코드워드는 낮은 SNR에서도 일부 비트가 변형되더라도 전체적인 패턴을 유지하여 다른 코드에 비해 높은 성능을 유지할 수 있다. 반면, BCH(15,7)와 RM(16,11) 코드는 코드워 드 길이가 Golay 코드보다 짧고, 중복성이 적으며 패턴 이 단순하다. 이로 인해 높은 SNR에서는 구조가 간단 하고 코드워드 길이가 짧은 BCH와 RM 코드를 CRANet이 더 쉽게 학습하고 구별할 수 있어 Golay 코드보다 높은 정확도를 보인다. 그러나 낮은 SNR에서 는 잡음이 증가하여 Golay 코드로 잘못 인식되는 결과 를 보인다. 결과적으로 그림 7은 CRANet2D이 높은 SNR뿐만 아니라 낮은 SNR에서도 특정 코딩 종류에 대해 매우 우수한 인식 성능을 발휘함을 입증한다.
그림 8은 CRANet1D의 SNR에 따른 혼동행렬을 보 여준다. 그림 8(a)는 10dB의 결과로, CRANet2D와 마찬 가지로 Golay코드를 제외한 7가지 코드가 모두 100% 의 정확도를 보였다. 하지만 그림 8(b)와 (c)에서 확인 할 수 있듯이, 낮은 SNR에서는 CRANet2D보다 성능이 크게 저하되었다. 특히 Polar, Hamming 그리고 Product 코드를 제외한 나머지 코드들은 SNR이 낮아 질수록 정확도가 급격히 떨어지는 경향을 보였다. 이는 CRANet2D와 같이 코드워드가 긴 코드들과 비블록 코 드인 Convolution과 Turbo 코드를 인식하는 데 어려움 이 있음을 알 수 있다.
표 6은 Attention mechanism을 적용한 모델과 적용 하지 않은 모델의 정확도를 비교하는 표이다 . 비교결과, Attention mechanism을 적용한 CRANet2D와 CRANet1D 모델의 정확도가 적용하지 않은 모델 보다 각각 3.12%와 3.96% 높았다. 이를 통해 Attention mechanism이 채널코딩 인식에 효과적으로 기여했음을 확인할 수 있다.
표 6.
| Model | Average accuray |
|---|---|
| CRANet2D | 96.34% |
| CRANet2D (w/o A) | 93.22% |
| CRANet1D | 78.74% |
| CRANet1D (w/o A) | 74.78% |
표 7은 CRANet의 파라미터 수, 모델 크기 그리고 추론 시간을 측정한 결과이다. CRANet2D의 모델 크기 는 45.46MB로 CRANet1D의 4.59MB보다 약 10배 정 도 크다. 추론 속도는 CRANet2D는 0.1213ms로 CRANet1D의 0.0269보다 약 4.51배 정도 느리다. 이 같 은 차이는 CRANet2D는 2D CNN 모델이며, 입력 데이 터 역시 2차원으로 처리되는 구조 때문이다. 비록 CRANet2D가 CRANet1D에 비해 하드웨어적 효율은 낮 지만, 모델의 크기가 45.46MB로 과도하게 큰 편은 아 니며, 추론 속도도 0.1213ms로 실시간 무선 환경에서 도 활용 가능하다.
Ⅳ. 결 론
본 논문은 채널코딩 종류 및 파라미터 정보가 없는 블라인드 상황에서, 채널코딩 인식을 위한 딥러닝 모델 을 제안한다. 딥러닝 모델은 CRANet으로, CNN Residual, Channel Attention 그리고 Spatial Attention 으로 구성한다. Atention 기법은 특징맵의 채널 중요도 와 공간적 위치 정보를 강조하는 역할을 한다. 실험에 사용한 채널코딩 종류는 8가지로 BCH(15, 7), Hamming(8,4), Product(8,4), RM(16,11), Polar(8, 4), Golay(23,12), Convolution(2,1,5), Turbo(3,1, 4)이다.
시뮬레이션 결과, SNR에 따른 정확도 그래프에서 CRANet이 벤치마크 딥러닝 모델인 TextCNN, CNN-LSTM보다 매우 우수한 성능을 보였다. 또한, 2D CNN을 사용한 CRANet2D는 0dB에서 93.62%를 기록 하며, 69.22%를 기록한 1D CNN 기반 CRANet1D보다 높은 정확도를 나타냈다. 이는 채널코딩 인식에서 1D CNN보다 2D CNN이 더 유리함을 의미한다. 혼동행렬 을 통한 채널코딩 별 정확도 분석을 통해, 코드워드가 길수록 인식 정확도가 낮아짐을 보였다.
Biography
References
- 1 S. Jeong and J. Lee, "Performance of bit-patterned media recording system according to LDPC coding structures," J. KICS, vol. 45, no. 1, pp. 1-6, Jan. 2020. (https://doi.org/10.7840/kics.2020.45.1.1)doi:[[[10.7840/kics.2020.45.1.1]]]
- 2 H. Cho, M. Chae, and W. Lim, "Implementation of modulation and channel coding recognition using CNN and protocol reverse engineering simulation in blind communication environment," J. KICS, vol. 49, no. 11, pp. 1644-1657, Nov. 2024. (https://doi.org/10.7840/kics.2024.49.11.1644)doi:[[[10.7840/kics.2024.49.11.1644]]]
- 3 Y. Liu and F. Wang, "Blind data detection with unknown channel coding," IEEE Commun. Lett., vol. 24, no. 4, pp. 758-761, Apr. 2020. (https://doi.org/10.1109/LCOMM.2020.296453 9)doi:[[[10.1109/LCOMM.2020.2964539]]]
- 4 Y. Wang, W. Zhang, L. Shi, Y. Chang, and Y. Lui, "Blind recognition of RS codes based on channel condition determination," IEEE Commun. Lett., vol. 28, no. 5, pp. 1132-1136, May 2024. (https://doi.org/10.1109/LCOMM.2024.337228 8)doi:[[[10.1109/LCOMM.2024.3372288]]]
- 5 L. Shi, W. Zhang, Y. Chang, H. Wang, and Y. Lui, "Blind recognition of reed-solomon codes based on galois field fourier transform and reliability verification," IEEE Commun. Lett., vol. 27, no. 8, pp. 2137-2141, Aug. 2023. (https://doi.org/10.1109/LCOMM.2023.328560 7)doi:[[[10.1109/LCOMM.2023.3285607]]]
- 6 X. Qin, S. Peng, X. Yang, and Y. D. Yao, "Deep learning based channel code recognition using TextCNN," in 2019 IEEE Int. Symp. DySPAN, pp. 1-5, Dec. 2019. (https://doi.org/10.1109/DySPAN.2019.893580 5)doi:[[[10.1109/DySPAN.2019.8935805]]]
- 7 B. Shen, C. Huang, W. Xu, T. Yang, and S. Cui, "Blind channel codes recognition via deep learning," IEEE J. Selected Areas in Commun., vol. 39, no. 8, Aug. 2021. (https://doi.org/10.1109/JSAC.2021.3087252)doi:[[[10.1109/JSAC.2021.3087252]]]
- 8 S. Zhang, L. Zhou, Y. Tang, L. Wang, and Q. Chen, "Blind recognition of channel coding based on CNN-BLSTM," in 2021 IEEE ICNSC, vol. 1, pp. 1-5, Feb. 2022. (https://doi.org/10.1109/ICNSC52481.2021.970 2153)doi:[[[10.1109/ICNSC52481.2021.9702153]]]
- 9 K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," in Proc. IEEE Conf. CVPR, pp. 770-778, Dec. 2016.custom:[[[-]]]
- 10 S. Woo, J. Park, J. Lee, and I. Kweon, "CBAM: Convolutional block attention module," in Proc. ECCV, pp. 3-19, Sep. 2018. (https://doi.org/10.48550/arXiv.1807.06521)doi:[[[10.48550/arXiv.1807.06521]]]
- 11 B. J. Singstad and C. Tronstad, "Convolutional neural network and rule-based algorithms for classifying 12-lead ECGs," in 2020 Comput. in Cardiology, pp. 1-4, Feb. 2021. (https://doi.org/10.22489/CinC.2020.227)doi:[[[10.22489/CinC.2020.227]]]
- 12 S. Huang, J. Tang, J. Dai, and Y. Wang, "Signal status recognition based on 1DCNN and its feature extraction mechanism analysis," Sensors, vol. 19, no. 9, Apr. 2019. (https://doi.org/10.3390/s19092018)doi:[[[10.3390/s19092018]]]
- 13 W. Yuan, and S. Che, "Blind recognition of 5G LDPC codes over a candidate set," IEEE Comm. Lett., vol. 28, no. 4, pp. 744-748, Apr. 586 2024. (https://doi.org/10.1109/LCOMM.2024.335985 6)doi:[[[10.1109/LCOMM.2024.3359856]]]
- 14 L. Kai, Y. Cao, and Y. Lv, "Blind recognition of channel codes based on a multiscale dilated convolution neural network," Physical Commun., vol. 64, pp. no. 102365, Jun. 2024. (https://doi.org/10.1016/j.phycom.2024.102365)doi:[[[10.1016/j.phycom.2024.102365]]]