Yelan Lee♦ and Juyeop Kim°
An Adaptive Channel Equalization Scheme for Interference-Robust Secondary Synchronization Signal Detection in LTE and 5G Systems
Abstract: This paper proposes a method to enable effective cell ID detection by UE during the synchronization process in LTE and 5G networks under interference conditions. To enhance the SSS detection performance, equalization is performed using channel estimation values obtained through the PSS. However, in environments where interference signals from neighboring base stations are present, equalization may degrade performance. Therefore, this study mathematically analyzes and presents an adaptive equalization technique that detects interference and optimizes SSS detection when multiple base station signals are received. A hardware testbed is built to validate the proposed method, demonstrating reliable cell ID detection even in the presence of interference signals.
Keywords: Cell search , equalization , SSS detection , software modem , interference
이예란♦, 김주엽°
LTE 및 5G 시스템에서 간섭에 강인한 2차 동기신호 검출을 위한 적응적 채널 보상 기법
요 약: 본 논문은 LTE, 5G 동기화 과정에서 간섭 신호 환경일 때 User Equipment(UE)가 기지국으로부터의 효과적으로 cell ID를 검출하기 위한 기법을 제안한다. Cell ID 검출 과정 중 Secondary Synchronization Signal(SSS) 검출 성능 향상을 위해 Primary Synchronization Signal(PSS) 기반으로 획득한 채널 추정값을 사용하여 equalization 을 진행하는데, 인접 기지국으로부터 간섭 신호가 들어오는 환경에서는 equalization으로 인해 성능 열화가 발생할수 있다. 따라서 본 연구는 여러 기지국 신호가 수신될 때 간섭 신호를 감지하고 효과적인 SSS 검출을 위해equalization을 적응적으로 수행하는 기법을 수학적으로 분석하여 제시한다. 그리고 하드웨어 테스트베드를 구축하여 제안 기법을 통해 간섭 신호 환경에서도 신뢰성 높은 cell ID 검출을 진행할 수 있음을 실험을 통해 검증한다.
Ⅰ. 서 론
일상생활에서 Long Term Evolution(LTE) 및 5th Generation mobile communications(5G)의 사용 빈도수가 잦은 만큼 기지국과 UE 사이의 효율적인 무선 접속 연결은 중요한 과정이다[1,2]. 이를 위해 UE로부터 진행되는 cell search 과정은 필수이다. Cell search는 UE가 자신이 속한 cell을 정확히 식별하고 해당 cell의 기지국 네트워크에 접속하여 초기 연결 설정을 준비하는 과정이다. 이 과정에서 UE는 적절한 주파수 대역을 찾으면서 시간 및 주파수 동기를 대상 기지국에 맞춤으로써 이후 기지국과의 통신을 효율적으로 시작할 수 있다. 또한 cell search는 UE로 하여금 최적의 기지국과 통신 연결을 설정하게 하므로 전반적인 네트워크 연결에 대한 품질에 결정적인 요인으로 작용한다.
Cell search에서 UE의 동기화는 핵심적인 신호처리 과정이다. LTE 및 5G 시스템에서는 기지국이 Down Link(DL) 채널을 통해 PSS, SSS를 전송하며 UE에서 이를 검출하는 형태로 동기화가 이루어진다. 이 동기화 과정에서 간섭, multi-path fading, 시간 및 주파수 오프셋 등 다양한 왜곡 요인으로 인해 검출 성능 열화가 발생할 수 있으므로 이에 대해 필수적으로 보상이 이루어져야 한다[3-5]. 특히 SSS에 대한 검출은 주파수 축에서 이루어질 뿐 아니라 다수의 대상 후보로부터 식별해야 하므로 신호 왜곡에 가장 민감한 과정이다[6,7]. 따라서 전체 cell search의 정확도를 개선하기 위해서는 SSS에 대한 검출 과정이 더욱 정교하게 진행되어야 한다.
기존 cell search 관련 연구는 Cell specific reference signal을 통해 추정한 Physical Cell ID(PCI)를 제어하여 cell search의 신뢰성 향상을 목표로 진행하였다[8]. 또한, cell range 확장이 초기 PCI 검출 확률 및 시간에 미치는 영향[9]과 PCI detection 시간 단축을 위해 Integer Frequency Offset(IFO)과 SSS sequence의 joint estimation을 사용하는 알고리즘에 대한 연구가 진행되었다[10].
한편, Orthogonal Frequency Division Multiplexing(OFDM) 시스템에서 Channel Equalization(CE)은 주파수 축 심볼에 대한 핵심 보상 과정에 해당한다. 전송 경로에서 진폭 및 위상에 대한 왜곡이 발생하였을 때, CE를 통해 수신 심볼을 보상하여 원래의 심볼로 복원하게 된다. 일반적으로 cell search 과정에서도 수신된 PSS를 기반으로 SSS 심볼에 대한 CE를 수행할 수 있다[11]. 즉, SSS 검출 전에 CE를 통해 수신 SSS 심볼에 대한 보상을 수행하여 SSS 검출 성능을 개선할 수 있다.
기존 cell search 과정에서 CE 관련 연구는 이상적인 Synchronization Channel(SCH) 구조 설계를 위해 다양한 시스템 환경에서의 성능을 비교하였다[12]. 그리고 PSS와 SSS의 채널 차이[13], 인접 neighbor cell search 과정[14], Up Link(UL) 간의 간섭 및 CFO 문제로 인한 성능 저하에 대한 연구가 진행되었다[15]. 또한, 동기화 과정에서의 복잡성 감소[16-20] 및 인접 기지국의 간섭 신호 검출을 최소화하여 성능을 높이는 연구도 이루어졌다[21].
그러나 하나의 UE가 여러 기지국에 해당하는 신호를 수신할 경우, CE 과정에서 오히려 원래 송신 심볼의 복원이 어려워진다. 수신된 PSS 신호를 통한 채널 추정 값을 사용하여 CE를 수행하지만, 인접 기지국 신호의 간섭으로 채널 값이 부정확해지면서 CE가 완벽하게 진행되지 않는다. 이는 심볼간의 상관관계 도출에 영향을 미치며 결과적으로 SSS 검출 성능이 저하된다. 따라서 cell search 과정에서 간섭 문제를 완화할 수 있는 기법이 필요하다.
Cellular system에서 간섭을 완화하기 위한 다양한 기술이 제안되었다. 현재 존재하는 기술로는 Other Cell Interference(OCI) 완화[22], Interference Cancellation(IC) 기술[23], multi-cell 환경에서 noise 향상을 억제할 수 있는 기술이 제안되었다[24]. 또한, Cyclic Prefix(CP)의 반복적인 속성을 활용하여 OCI 감소 기법[25]이 제안되었다. 그리고 각 UE에 할당된 Resource Block(RB)의 전력 최적화를 통한 Inter-Carrier Interference(ICI) 감소 기법[26], 간섭 전력과 수신신호 전력을 비교하여 간섭 기지국을 식별하는 기법도 제안되었다[27]. 추가적으로 특정 sequence를 통해 상관값을 계산하여 multi-path 및 ICI를 줄이는 연구도 진행되었다[28].
Cell search 동기화 과정에서 간섭 신호를 제거하는 연구도 진행되었다. 해당 연구는 LTE에서 이전에 검출한 cell의 간섭 신호를 제거하여 다음 cell에 대한 검출 성능을 향상시키는 기법을 제안했다. 그러나 신호를 삭제하는 과정에서 계산 복잡도 및 시간이 증가할 수 있다[29]. Cell reference signal 대신 Physical Broadcast Channel(PBCH)을 사용하여 ICI가 없는 채널을 추정하는 기법도 제안되었으나, 해당 cell의 동기 신호들을 재구성하여 인접 cell을 검출하는 추가적인 절차가 필요하다[30]. 또한, 간섭 신호를 재구성 후 수신된 신호에서 삭제하는 기술은 간섭 신호의 재구성 과정에서 계산 복잡도가 증가할 수 있다[31]. 동기화 시 전력 최적화를 위한 논리 회로연구 중 연속된 SSS의 상관관계를 출력하여 간섭의 영향을 줄일 수 있는 연구가 진행되었으나 상용 신호에 대한 적용 근거가 부족하다[32]. 5G cell search 동기화 과정에서도 cell 경계에 위치한 UE가 SSS 검출 성능을 향상시키기 위해 second threshold 값을 활용하는 연구가 진행되었으나, 해당 연구 또한 second threshold 값에 대한 peak 값 계산 복잡도가 증가할 수 있다[33].
기존 연구들은 간섭 환경에서 channel 보상으로 발생하는 문제에 대한 고찰이 부족하다. 특히, 인접 기지국의 간섭 신호가 존재하는 상황에서 적용이 불확실하다. 즉, 간섭 환경에서 equalization으로 인해 검출 성능이 저하되는 문제는 여전히 존재한다. 따라서 LTE와 5G의 cell search에서 기지국 간의 간섭 문제를 극복하여 동기화에 특화된 효율적인 channel 보상 과정이 필요하다고 볼 수 있다[34,35].
이를 바탕으로, LTE 및 5G 환경에서 다양한 기지국의 cell 신호가 수신하는 UE가 간섭 신호의 영향을 최소화해야 한다. 또한, 성능 열화를 방지하고 효율적인 동기화를 위해 적응적인 equalization 알고리즘이 필요하다. 따라서 본 논문에서는 인접 기지국 신호가 존재하는 환경에서 cell search 동기화 작업 중, PSS 검출로부터 얻어진 채널 추정값을 사용한 equalization 과정의 문제점과 제안 기법을 수학적으로 분석한다. 더불어, 제안 기법의 성능을 상용 신호 환경에서 다양한 실험을 통해 평가하고 입증한다. 이를 통해 본 연구로부터 다음과 같은 기대효과를 예상한다.
- LTE와 5G 표준에 모두 적용 가능한 통합적인 모델 제시
기존의 분리된 접근 방식과 달리, LTE와 5G 표준에 공통으로 적용할 수 있는 수학적 분석을 통해 문제를 정의했다. 현 5G는 기존 LTE 망 기반의 Non Stand Alone(NSA) 형태이므로 두 시스템이 공존하는 환경에 효율적으로 적용 가능한 기법을 필요로 한다. 이에 맞게 두 시스템의 요소들을 공통 변수로 정의하고 수학적으로 일반화하였다.
- 간섭 신호를 고려한 성능 개선을 위한 새로운 기법 제시
기존 연구를 보완하여 인접 기지국의 간섭 신호 영향을 최소화하는 적응적인 채널 보상 기법을 제안했다. 수학적 분석을 통해 간섭 신호 환경에서 동기화 과정 중의 문제점 도출 후, 새로운 기법을 설계하였다. 실제 모뎀에 적용할 수 있도록 알고리즘을 설계하여 효율적으로 cell search를 수행할 수 있다.
- 상용화를 위한 실제 구현
제안 기법을 상용 환경에서 구현하여 여러 테스트베드를 통해 실시간 동작 및 실제 채널에서 성능을 평가하였다. 이는 본 연구 및 관련 연구의 향후 상용화 과정에서 성능과 안정성을 보장하는데 중요한 역할을 할 수 있다.
본 논문의 2장에서는 LTE 및 5G의 신호 시스템 모델을 설계했다. 3장에서는 간섭 환경에서의 채널 보상 기법을 수학적으로 분석하여 문제점과 해결방안을 제시하였으며, 4장에서는 설계한 알고리즘을 실제 환경에서 구현하여 성능을 평가했다. 마지막으로 5장에서는 본 논문의 제안 기법 및 연구 결과를 요약하였다.
Ⅱ. 시스템 모델
본 장에서는 LTE 및 5G를 아우르는 cell search 시스템 모델을 소개한다. cell search를 위한 Synchronization Signal(SS) 및 OFDM 시스템 기반의 송수신 신호처리 및 채널 모델 등의 내용을 정리한다.
2.1 LTE·5G의 변·복조 및 채널 신호 모델
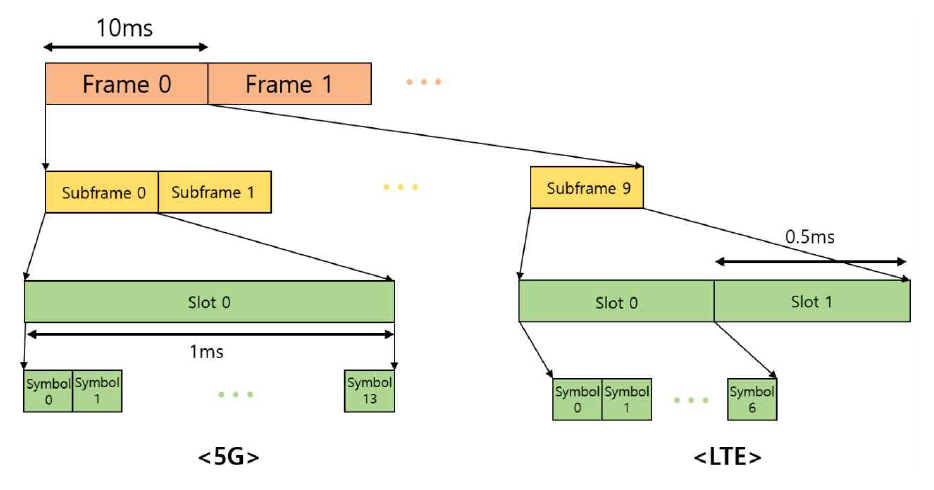
그림 1은 본 연구에서 가정하는 LTE와 5G의 프레임 구조 예시를 도식화해서 나타내고 있다. LTE와 5G 모두 한 프레임은 10개의 서브 프레임으로 구성된다. 5G의 경우 μ(numerology)에 따라 서브 프레임 내 slot의 개수 및 길이가 달라지게 된다. 가령 μ가 0인 경우, 1개의 슬롯이 한 서브 프레임을 구성하며 슬롯 길이는 1ms가 된다. 이때 한 슬롯은 14개의 OFDM 심볼로 구성된다. 반면 LTE의 경우, 항상 2개의 slot이 한 서브 프레임을 구성한다. 한 슬롯은 0.5ms 길이를 가지며, 7개의 OFDM 심볼로 구성된다.
기지국에서는 전송하고자 하는 심볼에 대해 N-point Inverse Fast Fourier Transform (IFFT) 과정을 거쳐 송신하고자 하는 OFDM 심볼을 생성한다. N-point IFFT를 [TeX:] $$F_N^{-1}\{\cdot\}$$라 정의하면, [TeX:] $$F_N^{-1}\{X[k]\}[n]=\frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j \frac{2 \pi}{N} k n}$$가 성립한다. 그리고 [TeX:] $$x[n]$$는 송신 OFDM 심볼, [TeX:] $$X[k]$$를 k번째 부반송파에 변조되는 전송 심볼이라 정의하면 [TeX:] $$x[n]$$는 송신 OFDM 심볼일 때 IFFT OFDM 변조 과정은 수학적으로 다음과 같이 표현될 수 있다.
송신 신호는 Rayleigh fading 및 Additive White Gaussian Noise(AWGN)가 고려된 채널 모델을 통해 UE에 수신된다고 가정한다. 채널 임펄스 응답을 [TeX:] $$h[n]$$으로 정의하면, UE의 수신 신호 [TeX:] $$y[n]$$는 다음과 같이 나타낼 수 있다.
여기서 ⊗은 linear convolution 연산이고 [TeX:] $$w[n]$$은 분산이 [TeX:] $$\sigma^2$$인 AWGN이다. UE에서는 일반적으로 전송된 심볼을 획득하기 위해서 수신 신호에 대해 N-point Fast Fourier Transform (FFT)을수행한다. N-point FFT를 [TeX:] $$F_N\{\cdot\}$$이라 정의하면 [TeX:] $$F_N\{x[n]\}[k]=\sum_{n=0}^{N-1} x[n] e^{-j \frac{2 \pi}{N} k n}$$가 성립한다. 그리고 채널 주파수 응답을 [TeX:] $$H[k], Y=F_N\{y[n]\}$$라 정의하면 수신 신호는 아래 식과 같이 표현될 수 있다.
여기서 [TeX:] $$W[k]$$는 k번째 부반송파에 대한 AWGN이다. 식 (3)을 행렬 형태로 표현하면 아래와 같다.
여기서 X는 송신 신호, H는 채널, W는 AWGN, Y는 수신 신호를 나타내는 행렬이며 다음과 같이 정의된다.
(5)
[TeX:] $$\begin{aligned} X & =[X[0], X[1], \cdots, X[N-1]]^T \\ H & =\operatorname{diag}[H[0], H[1], \ldots, H[N-1]] \\ W & =[W[0], W[1], \cdots, W[N-1]]^T \\ Y & =[Y[0], Y[1], \cdots, Y[N-1]]^T \end{aligned}$$2.2 LTE·5G의 동기신호 모델 및 수신 처리 과정
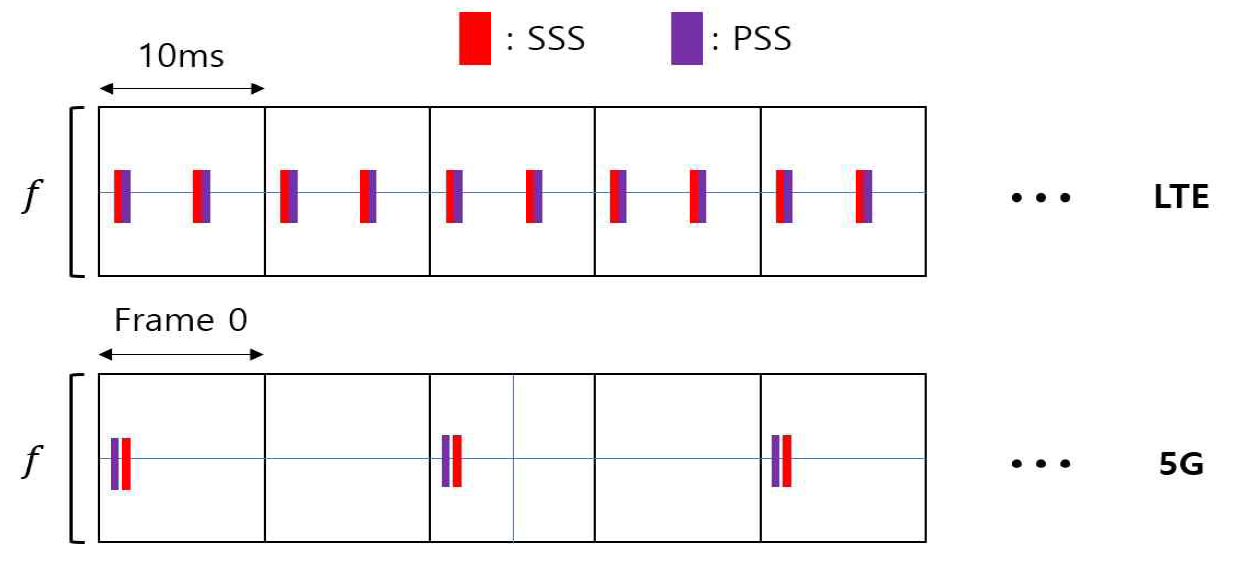
그림 2는 LTE 및 5G에서의 동기신호 전송을 도식화한 것이다. SS는 LTE의 경우 프레임 내에 고정적인 시간 및 주파수 지점에 위치하고 5G의 경우 프레임 내에 유동적으로 위치할 수 있는 SS Block (SSB) 내에 존재한다. 이때 5G는 1개의 Beam을 쓴다고 가정하면 두 frame 당 동기신호 1 set가 전송된다. 한편 LTE의 경우 한 frame 당 동기신호 2 set가 전송된다. 또한, 5G의 경우PSS가 SSS보다 먼저 전송되며 LTE의 경우 SSS보다 PSS가 먼저 전송된다.
그림(Fig.) 2.
LTE 및 5G를 아우르는 일반 OFDM 시스템에 대한 동기 신호 모델을 수학적으로 표현하기 위해서, slot 내 PSS가 포함된 OFDM 심볼의 index를 [TeX:] $$\lambda_{P S S},$$ SSS가 포함된 OFDM 심볼의 index를 [TeX:] $$\lambda_{S S S},$$로 정의한다. LTE의 경우, SSB가 시작되는 OFDM 심볼 index를 [TeX:] $$\lambda_{S S B},$$라 할 때 [TeX:] $$\lambda_{P S S}=6$$이며 [TeX:] $$\lambda_{S S S}=5$$가 된다. 5G의 경우, [TeX:] $$\lambda_{P S S}=\lambda_{S S B}$$이며 [TeX:] $$\lambda_{S S S}=\lambda_{S S B}+2$$가 된다.
또한 시간 축에서의 PSS와 SSS간 거리를 고려하기 위해서 [TeX:] $$\Delta \lambda_{P S}=\left|\lambda_{S S S}-\lambda_{P S S}\right|$$로 정의한다. LTE 및 5G의 경우 [TeX:] $$\Delta \lambda_{P S}$$는 각각 1 및 2가 된다.
LTE 및 5G의 동기신호 전송 모델을 일반화하여 수학적으로 표현할 수 있다. i번째 PSS 및 SSS 수열을 [TeX:] $$\alpha_i \text { 와 } \beta_i$$로 정의하면, LTE 및 5G를 아우르도록 다음과 같이 나타낼 수 있다.
(7)
[TeX:] $$\beta_i=\left[Q_{i, 0}^S, \cdots, Q_{i, l-1}^S\right]\left(0 \leq i \leq L_S-1\right)$$여기서 [TeX:] $$Q_{i, j}^P \text { 와 } Q_{i, j}^S$$는 각각 i번째 PSS 및 SSS 수열에 포함되는 j번째 심볼 [TeX:] $$\left(\left|Q_{i, l}^P\right|=1,\left|Q_{i, l}^S\right|=1\right),$$ l은 각 수열의 길이로 LTE의 경우 63, 5G의 경우 127과 같다. 그리고 [TeX:] $$L_S$$는 SSS 수열의 종류로, LTE 및 5G의 경우 각각 168 및 336이 된다[36,37].
식 (6), (7)에 정의된 수열은 지정된 부반송파에 할당 되어 전송된다. i번째 PSS 및 SSS 수열이 할당된 k번째 부반송파 심볼을 각각 [TeX:] $$X_i^{P S S}[k], X_i^{S S S}[k]$$라고 정의하면 LTE 및 5G에 대해 일반적으로 다음과 같이 나타낼 수 있다.
(8)
[TeX:] $$X_i^{P S S}[k]= \begin{cases}Q_{i, k+\frac{(l+1)}{2}}^P & \left(0 \leq k \leq \frac{l-1}{2}\right) \\ Q_{i, k-N-\frac{l-1}{2}}^P & \left(N-\frac{l-1}{2} \leq k \leq N-1\right) \\ 0 & \text { otherwise }\end{cases}$$
(9)
[TeX:] $$X_i^{S S S[k]}= \begin{cases}Q_{i, k+\frac{(l+1)}{2}}^S & \left(0 \leq k \leq \frac{l-1}{2}\right) \\ Q_{i, k-N-\frac{l-1}{2}}^S & \left(N-\frac{l-1}{2} \leq k \leq N-1\right) \\ 0 & \text { otherwise }\end{cases}$$LTE 및 5G 기지국은 [TeX:] $$X_i^{P S S}[k], X_i^{S S S}[k]$$에 대해 2.1절에서의 방식으로 OFDM 심볼을 생성 및 전송한다. 또한 동기화를 수행하는 UE는 2.1절에서 가정한 채널을 거쳐서 신호를 수신한다.
그림 3은 LTE 및 5G UE 측에서의 동기화 과정 흐름을 나타낸 것이다. UE는 우선 PSS를 처리하면서 SSS를 포함하는 OFDM 심볼의 위치를 파악하기 위한 슬롯 타이밍 오프셋을 검출한다. 또한 SSS 검출 성능 향상을 위해 PSS로부터 추정한 채널을 기반으로 equalization을 진행한다. 이후 UE는 SSS를 처리하면서 frame의 타이밍 오프셋을 검출한다. 두 가지 동기 신호의 수신 처리를 완료하면 기지국과의 시간 및 주파수 동기를 맞추면서 cell ID를 파악할 수 있다.
PSS 검출은 PSS 수열과의 auto-correlation을 기반으로 진행된다고 가정한다. PSS가 포함된 OFDM 심볼의 오프셋을 [TeX:] $$n_o$$로 정의하고, [TeX:] $$x_i^{P S S}=F^{-1}\left\{X_i^{P S S}[k]\right\}$$라 가정하면 다음 수식을 통해서 추정한다.
(10)
[TeX:] $$\left(n_o, N_{I D}^{(2)}\right)=\arg \max _{\tau, i}\left\{C_{P S S, i}[\tau]\right\}$$여기서 [TeX:] $$C_{P S S, i}[\tau]$$은 auto - correlation의 결과로 다음과 같이 정의된다.
이후 UE는 [TeX:] $$n_{\text {start }}$$를 기반으로 SSS를 주파수 축에서 검출한다. 이를 위해서 수신된 PSS 심볼을 기반으로 k번째 부반송파에 대한 채널 추정인 [TeX:] $$\tilde{H}[k]$$를 도출한다.
[TeX:] $$y_{P S S}[n]=y\left[n+n_0\right], n=0,1, \cdots, N-1$$이라 가정하고 [TeX:] $$Y_{P S S}=F\left\{y_{P S S}[n]\right\}$$라 정의하면 zero-forcing을 기반으로 다음과 같이 [TeX:] $$\tilde{H}[k]$$를 추정한다.
이후 추정된 채널을 기반으로 수신된 SSS 심볼에 대한 채널 보상을 진행한다.
[TeX:] $$y_{S S S}[n]=y\left[n+n_{\text {start }}+N\left(\lambda_{S S S}-\lambda_{P S S}\right)\right], n=0,1,\cdots,N-1$$이라 가정하고 [TeX:] $$Y_{S S S}=F\left\{y_{S S S}[n]\right\}$$라 정의한다. 그리고 PSS와 SSS 검출의 시간차로부터 [TeX:] $$\tilde{H}[k]$$에서 발생하는 Carrier Frequency Offset(CFO)으로 인한 위상 차이를 θ라고 할 때, 수신된 SSS는 다음과 같이 나타낼 수 있다.
식 (12), (13)를 바탕으로 다음 수식을 통해 k번째 부반송파의 보상된 SSS 심볼인 [TeX:] $$\tilde{X}_{S S S}[k]$$을 획득한다.
이후 보상된 SSS 심볼과 SSS 수열 간 cross correlation을 통해 SSS를 최종적으로 검출한다. i번째 SSS 수열과의 cross-correlation을 [TeX:] $$C_{S S S, i}$$로 정의하면, 다음과 같이 수학적으로 나타낼 수 있다.
여기서 [TeX:] $$\tilde{Q}_j^S$$는 다음과 같이 정의된다.
(16)
[TeX:] $$\tilde{Q}_j^S= \begin{cases}\tilde{X}_{S S S}\left[N-\frac{l-1}{2}+j\right], & 0 \leq j \leq \frac{l-1}{2}-1 \\ \tilde{X}_{S S S}\left[j-\frac{l-1}{2}\right], & \frac{l-1}{2} \leq j \leq l-1\end{cases}$$최종적으로 SSS 검출을 아래 식을 통해 수행한다.
Ⅲ. 간섭에 적응적인 SSS 채널 보상 기법
본 장에서는 간섭 환경에서 적응적으로 채널 보상을 진행하여 SSS 검출 성능을 향상시키는 기법을 제안한다. 즉, 간섭 환경을 인지하여 SSS 검출 전 수행되는 equalization 과정에 대한 적용 여부를 결정한다. 우선 간섭 환경에서의 채널 보상 동작이 SSS 검출 성능에 미치는 영향을 수학적으로 분석하고, 이를 기반으로 적응적 채널 보상 기법을 설계하도록 한다.
3.1 간섭이 없을 때 equalization 여부에 따른 SSS 검출 성능 분석
간섭 신호가 없을 때, equalization 처리가 된 SSS 수신 신호값인 [TeX:] $$\tilde{X}_{S S S}[k]$$는 식 (14)에 식 (13)을 대입하여 다음과 같이 나타낼 수 있다.
(18)
[TeX:] $$\begin{aligned} \tilde{X}_{S S S}[k]=Y_{S S S}[k] \tilde{H}[k]= & X_{N_{I D}^{(1)}}^{S S S}[k]|H[k]|^2 e^{j \Delta \theta} \\ & +W_{S S S}[k] H^*[k] \\ & +W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S]}[k] X_{N_{I D}^{(2)}}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & +W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(2)}}^{P S S}[k] \end{aligned}$$획득된 [TeX:] $$\tilde{X}_{S S S}[k]$$를 바탕으로 SSS 검출을 위해 각 SSS 수열에 대한 correlation이 계산된다. 이 과정에서 실제 송신된 [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열의 k번째 부반송파에 대한 complex conjugate multiplication은 다음과 같이 계산 된다. 이때 SSS 심볼의 진폭이 1임을 가정한다[35,36].
(19)
[TeX:] $$\begin{aligned} \tilde{X}_{S S S}[k] \cdot & X_{N_{I D}^{(1)}}^{S S S^*}[k]= \\ & |H[k]|^2 e^{j \Delta \theta}+W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*} H^*[k] \\ & +W_{P S S}^*[k] X_{N_{I D}^2}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & +W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k] \end{aligned}$$식 (19)를 기반으로 K개의 부반송파들에 대해 [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열과 correlation을 수행한 결과인 [TeX:] $$C_1$$는 다음과 같이 나타낼 수 있다.
(20)
[TeX:] $$\begin{aligned} C_1=\sum_{k=1}^K\left(\tilde{X}_{S S S}[k]\right. & \left.\cdot X_{S S S}^*[k]\right)= \\ \sum_{k=1}^K|H[k]|^2 e^{j \Delta \theta} & +\sum_{k=1}^K\left(W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] H^*[k]\right. \\ & +W_{P S S}^*[k] X_{N_{I D}^{(2)}}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & \left.+W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k]\right) \end{aligned}$$한편, equalization을 하지 않고 SSS 검출을 진행하면 [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열의 번째 부반송파에 대한 complex conjugate multiplication은 다음과 같이 나타낼 수 있다.
(21)
[TeX:] $$Y_{S S S}[k] \cdot X_{N_{I D}^{(1)}}^{S S S^*}[k]=H[k] e^{j \Delta \theta}+W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k]$$[TeX:] $$C_1$$를 근사화한 것과 같은 방식으로, [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열에 대한 cross-correlation 결과인 [TeX:] $$C_2$$는 다음과 같이 나타낼 수 있다.
(22)
[TeX:] $$\begin{aligned} C_2= & \sum_{k=1}^K\left(Y_{S S S}[k] \cdot X_{N_{I D}^{(1)}}^{S S S^*}[k]\right)= \\ & \sum_{k=1}^K H[k] e^{j \Delta \theta}+\sum_{k=1}^K\left(W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k]\right) \end{aligned}$$각 correlation 결과의 Signal-to-Noise Ratio(SNR) 비교를 통해 간섭이 없을 때 equalization 여부가 SSS 검출에 어떤 영향을 미치는지 유추할 수 있다. 이때
(23)
[TeX:] $$S N R_{C_1}=\frac{K \cdot E\left[|H[k]|^4\right]}{E\left[|H[k]|^2\right]\left(E\left[\left|W_{P S S}[k]\right|^2\right]+E\left[\left|W_{S S S}[k]\right|^2\right]\right)+E\left[\left|W_{P S S}[k]\right|^2\left|W_{S S S}[k]\right|^2\right]}$$SNR은 [TeX:] $$\frac{E\left[s(t)^2\right]}{E\left[n(t)^2\right]}$$이며, [TeX:] $$C_1$$의 SNR은 식 (23)으로 나타낼 수 있다.
equalization 거치지 않았을 때의 [TeX:] $$S N R_{C_2}$$ 값은 다음과 같이 나타낼 수 있다.
(24)
[TeX:] $$S N R_{C_2}=\frac{K \cdot E\left[|H[k]|^2\right]}{E\left[\left|W_{S S S}[k]\right|^2\right]}$$이때, 신호 세기가 충분히 크다고 가정하고 [TeX:] $$E\left[|W|^2\right] \approx \sigma^2$$로 근사화하여 식 (23) 및 (24)를 다음과 같이 나타낼 수 있다.
correlation 후 SNR인 effective SNR 및 하나의 부반송파에 대한 SNR을 각각 [TeX:] $$S N R_e \text { 및 } S N R=\frac{E\left[|H[k]|^2\right]}{\sigma^2}$$로 정의하면 [TeX:] $$C_1 \text{과 } C_2 \text{와 } SNR_e$$에 대해 각각 식 (27) 및 (28)로 나타낼 수 있다.
위 식을 통해 equalization을 하지 않은 경우, 부반송파 간 위상 유사도가 높은경우 도달 가능한 [TeX:] $$S N R_e$$의 최대값은 [TeX:] $$K \cdot S N R$$이다. 그러나 위상 유사도가 낮을 경우, correlation 성능 열화를 일으킬 수준의 낮은 [TeX:] $$S N R_e$$에 도달할 수 있다. 반면 equalization을 진행하면 [TeX:] $$S N R_e$$이 항상 [TeX:] $$\frac{K}{2} \cdot S N R$$이 된다. 즉, equalization을 통해 최대 [TeX:] $$S N R_e$$이 절반으로 감소하면서도 안정적으로 유지되면서 신호 세기가 충분히 크면 안정적으로 correlation 결과를 얻을 수 있는 것을 의미한다. 결론적으로 간섭 신호가 존재하지 않을 때는 equalization을 거친 경우 SSS 검출이 더 높은 신뢰성을 가지는 것을 알 수 있다.
3.2 간섭이 존재할 때 equalization 여부에 따른 SSS 검출 성능 분석
서로 다른 PSS를 전송하는 인접 기지국의 간섭 신호가 수신될 때, 식 (12)와 같은 방식으로 추정된 채널을 다음과 같이 나타낼 수 있다.
(29)
[TeX:] $$\begin{aligned} \tilde{H}[k] & =Y_{P S S}[k] X_{N_{l D}^{(2)}}^{P S S^*}[k] \\ & =H[k]+H_I[k] X_I^{P S S}[k] X_{N_{l D}^{(2)}}^{P S S^*}[k]+W_{P S S}[k] X_{N_{I D}^{(2)}}^{P S S^*}[k] \end{aligned}$$여기서 [TeX:] $$H_I[k] \text { 및 } X_I^{P S S}[k]$$는 각각 인접 기지국 간의 채널 및 PSS이며 [TeX:] $$I \in 0,1,2 \text { 이고 } I \neq N_{I D}^{(2)}$$이다. 즉, 간섭 신호로 인해 원래 채널 추정값에 [TeX:] $$H_I X_{P S S, I} X_{P S S}^*$$가 추가로 더해지는 형태가 된다. 인접 기지국끼리 서로 다른 SSS를 전송할 때, 수신 SSS는 다음과 같이 나타낼 수 있다.
(30)
[TeX:] $$Y_{S S S}[k]=X_{N_{l l}^{11}}^{S S S}[k] H[k] e^{j \Delta \theta}+X_J^{S S S}[k] H_I[k] e^{j \Delta \theta_I}+W_{S S S}[k]$$여기서 [TeX:] $$\theta_I$$는 인접 기지국 신호로부터 CFO로 인한 위상 차이이며 [TeX:] $$X_J^{S S S}[k]$$는 인접 기지국이 송신한 SSS이고, [TeX:] $$J \in 0, \cdots, L_S-1 \text { 이며 } J \neq N_{I D}^{(1)}$$이다. 식 (29)의 [TeX:] $$\tilde{H}[k]$$로 equalization을 진행할 때 그 결과인 송신 SSS의 추정값 [TeX:] $$\widetilde{X}_{S S S}[k]$$을 다음과 같이 나타낼 수 있다.
(31)
[TeX:] $$\begin{aligned} & \tilde{X}_{S S S}[k]=Y_{S S S}[k] \tilde{H}^*[k]= \\ & X_{N_{I D}^{(1)}}^{S S S^*}[k]|H[k]|^2 e^{j \Delta \theta}+X_J^{S S S}[k] H^*[k] H_I[k] e^{j \Delta \theta} \\ & +W_{S S S}[k] H^*[k]+X_{N_{I D}^{(1)}}^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H[k] H_I^*[k] e^{j \Delta \theta} \\ & +X_I^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k]\left|H_I[k]\right|^2 e^{j \Delta \theta_I} \\ & +W_{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H_I^*[k] \\ & +W_{P S S}^*[k] X_{N_D^{(1)}}^{S S S}[k] X_{N_D^{(2)}}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & +W_{P S S}^*[k] X_{N_l^{(2)}}^{P S S}[k] X_J^{S S S}[k] H_I[k] e^{j \Delta \theta_I} \\ & +W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(2)}}^{P S S}[k] \end{aligned}$$[TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열의 k번째 부반송파에 대한 complex conjugate multiplication은 다음과 같이 계산된다.
(32)
[TeX:] $$\begin{aligned} & \tilde{X}_{S S S}[k] \cdot X_{N_{I D}^{(1)}}^{S S S ^*}[k]= \\ & |H[k]|^2 e^{j \Delta \theta}+H^*[k] H_I[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_I^{S S S}[k] e^{j \Delta \theta_I} \\ & +W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S *}[k] H^*[k] \\ & +X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H[k] H_I^*[k] e^{j \Delta \theta} \\ & +X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k]\left|H_I[k]\right|^2 e^{j \Delta \theta_I} \\ & +W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H_I^*[k] \\ & +W_{P S S}^*[k] X_{N_{I D}^{(2)}}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & +W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] H_I[k] e^{j \Delta \theta_I} \\ & +W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k] \end{aligned}$$식 (32)를 기반으로 K개의 부반송파들에 대해 [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열과 correlation을 수행한 결과인 [TeX:] $$C_1^{\prime}$$는 다음과 같이 나타낼 수 있다.
(33)
[TeX:] $$\begin{aligned} & C_1^{\prime}=\sum_{k=1}^K\left(\tilde{X}_{S S S}[k] \cdot X_{N_{I D}^{(1)}}^{S S S^*}[k]\right)= \\ & \sum_{k=1}^K|H[k]|^2 e^{j \Delta \theta}+\sum_{k=1}^K\left(H^*[k] H_I[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] e^{j \Delta \theta_I}\right. \\ & +W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] H^*[k] \\ & +X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H[k] H_I^*[k] e^{j \Delta \theta} \\ & +X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k]\left|H_I[k]\right|^2 e^{j \Delta \theta_I} \\ & +W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k] H_I^*[k] \\ & +W_{P S S}^*[k] X_{N_{I D}^{(2)}}^{P S S}[k] H[k] e^{j \Delta \theta} \\ & +W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] H_I[k] e^{j \Delta \theta_I} \\ & \left.+W_{S S S}[k] W_{P S S}^*[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_{N_{I D}^{(2)}}^{P S S}[k]\right) \end{aligned}$$한편, equalization을 하지 않고 SSS 검출을 진행했을 때 k번째 부반송파에 대해 다음과 같이 나타낼 수 있다.
(34)
[TeX:] $$\begin{aligned} Y_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] & =H[k] e^{j \Delta \theta}+X_{N_{ID}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] H_I[k] e^{j \Delta \theta_I} \\ & +W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] \end{aligned}$$[TeX:] $$C_1^{\prime}$$를 근사화한 것과 같은 방식으로 [TeX:] $$N_{I D}^{(1)}$$번째 SSS 수열에 대한 correlation 결과인 [TeX:] $$C_2^{\prime}$$는 다음과 같이 나타낼 수 있다.
(35)
[TeX:] $$\begin{aligned} & C_2^{\prime}=\sum_{k=1}^K Y_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] \\ & =\sum_{k=1}^K H[k] e^{j \Delta \theta} \\ & +\sum_{k=1}^K\left(X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] H_I[k] e^{j \Delta \theta_I}+W_{S S S}[k] X_{N_{I D}^{(1)}}^{S S S^*}[k]\right) \end{aligned}$$Noise 크기 계산 과정에서 pseudo-random 수열 간의 내적이 포함된 항을 다음과 같이 각각 [TeX:] $$\rho_1, \rho_2, \rho_3, \rho_4$$로 정의한다.
이때 equalization을 진행했을 때의 [TeX:] $$S N R_{C_1^{\prime}}$$ 값과 equalization을 진행하지 않았을 때의 [TeX:] $$S N R_{C_2^{\prime}}$$ 값은 3.1의 방식과 동일하게 식 (37) 및 (38)로 나타낼 수 있다.
(36)
[TeX:] $$\begin{aligned} \rho_1 & =\sum_{\substack{k=1, \\ k \neq m}}^K \sum_{\substack{m=1}}^K H^*[k] H_I[k] X_{N_{I D}^{(1)}}^{S S S^*}[k] X_J^{S S S}[k] H[m] H^*[m] X_{N_{I D}^{(1)}}^{S S S}[m] X_J^{S S S^*}[m] \\ \rho_2 & =\sum_{\substack{k=1, \\ k \neq m}}^K \sum_{m=1}^{K}X_{N_{I D}^{(2)}}^{PSS}[k] X_I^{P S S^*}[k] H[K] H_I^*[k] X_{N_{I D}^{(2)}}^{P S S^*}[m] X_I^{P S S}[m] H^*[m] H_I[m] \\ \rho_3 & =\sum_{\substack{k=1, \\ k \neq m}}^K \sum_{m=1}^{K}X_{N_{I D}^{(1)}}^{SSS^*}[k] X_J^{S S S}[k] X_{N_{I D}^{(2)}}^{P S S}[k] X_I^{P S S^*}[k]\left|H_I[k]\right|^2 X_{N_{I D}^{(1)}}^{S S S}[m] X_J^{S S S^*}[m] X_{N_{I D}^{(2)}}^{P S S^*}[m] X_I^{P S S}[m]\left|H_I[m]\right|^2 \\ \rho_4 & =\sum_{\substack{k=1, \\ k \neq m}}^K \sum_{m=1}^{K}X_{N_{I D}^{(1)}}^{SSS^*}[k] X_J^{S S S}[k] H_I[k] X_{N_{I D}^{(1)}}^{S S S}[m] X_J^{S S S^*}[m] H_I^*[m] \end{aligned}$$
(37)
[TeX:] $$S N R_{C_1^{\prime}}=\frac{K \cdot E\left[|H[k]|^4\right]}{E\left[\left|H_I[k]\right|^4\right]+2 E\left[\left|H_I[k]\right|^2\right] E\left[|H[k]|^2\right]+2 \sigma^2\left(E\left[\left|H_I[k]\right|^2\right]+E\left[|H[k]|^2\right]\right)+\sigma^4}$$
(38)
[TeX:] $$S N R_{C_2^{\prime}}=\frac{K \cdot E\left[|H[k]|^2\right]}{E\left[\left|H_I[k]\right|^2\right]+\sigma^2}$$여기서 pseudo-random 수열의 특성상 서로 다른 수열끼리 내적 결과값이 일정 수준 이하로 크지 않다는 점을 고려하여 K가 큰 값을 가질 때 [TeX:] $$\frac{\rho_1}{K}, \frac{\rho_2}{K}, \frac{\rho_3}{K}, \frac{\rho_4}{K} \approx 0$$이 성립한다고 가정한다. 여기서 [TeX:] $$B=\frac{E\left[\left|H_I[k]\right|^2\right]}{E\left[|H[k]|^2\right]}$$라고 정의할 때, 신호 세기가 충분히 큰 상황임을 가정하여 [TeX:] $$C_1^{\prime} \text{과 } C_2^{\prime} \text{의 } SNR_e$$에 대해 각각 식 (39) 및 (40)으로 나타낼 수 있다.
Equalization을 하지 않은 경우, 부반송파 간 위상 유사도가 높을수록 도달 가능한 [TeX:] $$S N R_e$$의 최대값은 [TeX:] $$\frac{K}{B}$$이다. 반면 equalization을 진행했을 때 [TeX:] $$\frac{K}{B^2+2 B}$$ 값에 도달할 수 있다. 즉, 항상 [TeX:] $$B \gt 0$$을 만족시키므로 [TeX:] $$C_1^{\prime}$$의 최대값은 [TeX:] $$C_2^{\prime}$$의 최대값의 [TeX:] $$\frac{1}{B+2}$$배이다. 따라서 [TeX:] $$C_1^{\prime}$$의 [TeX:] $$S N R_e$$ 값은 간섭량에 반비례하므로 간섭 신호가 존재할 때 equalization을 거치지 않은 경우가 오히려 더 신뢰성이 있는 SSS 검출 성능을 기대할 수 있는 것을 알 수 있다.
간섭 신호가 없는 경우, 수신한 SSS는 equalization을 통해 PSS 검출 시 획득한 대상 기지국 신호의 채널을 보상한다. 따라서 SSS 검출 시 대상 기지국의 신호로만 구성되며, 이때 SNR 값은 equalization을 진행하지 않은 경우보다 더 높게 나타난다. 이는 일반적인 equalization 과정을 통해 SSS 검출의 신뢰성을 높이는 결과를 반영한다. 반면, 간섭 신호가 존재할 경우, 수신된 SSS 및 PSS 검출을 통해 획득한 채널 신호에는 인접 기지국의 SSS 및 채널이 포함된다. 이러한 신호를 기반으로 equalization을 진행하면, correlation의 결과에 검출 대상 신호 외의 부수적인 요소들이 포함된다. 이로인해 SSS 검출 과정에서 인접 기지국의 간섭 신호가 noise 성분에 추가되며 SNR 값은 equalization을 진행하지 않았을 때보다 더 낮게 나타난다. 결과적으로 인접 기지국에 대한 간섭 채널 신호가 포함됨에 따라 equalization은 SSS 검출의 정상적인 작동을 저해할 수 있다. 따라서 간섭 신호가 감지되었을 때, 적응적으로 equalization을 진행하고 더 신뢰도가 높은 SSS 검출 결과를 채택하는 것이 필요하다.
3.3 적응적인 SSS 채널 보상 기법
본 논문에서 제안하는 적응적 채널 보상 기법은 앞에서 살펴본 간섭 영향에 대한 수학적 분석을 통해 간섭의 영향을 최소화하고 SSS 검출 성능을 극대화하는 것을 목적으로 한다. 우선 UE는 cell search 과정에서 PSS 검출 후, 간섭 신호 세기에 상응하는 임계값 [TeX:] $$C_{P S S, t h}$$을 기준으로 해당 기지국의 신호와 인접 기지국으로부터의 간섭 신호 유무를 감지한다. 그리고 간섭 신호가 존재할 경우, equalization 적용 여부에 따른 두 가지 correlation 값을 계산하고, 이를 비교하여 신뢰도가 높은 결과를 선택하도록 한다.
그림 4는 제안 기법의 알고리즘을 pseudo-code로 나타낸 것이다. 제안 기법의 알고리즘은 UE가 auto-correlation을 통해 PSS 검출을 진행하는 것으로 시작한다. 이 과정에서 UE는 최대값을 갖는 auto-correlation 결과를 기반으로 [TeX:] $$N_{I D}^{(2)} \text { 및 } n_0$$를 검출한다. 그리고 간섭 신호의 검출을 위해서 [TeX:] $$n_0$$을 중심으로 ω 시간 구간에서의 auto-correlation 결과를 관찰하면서 간섭 신호의 존재 여부를 결정한다. 이는 correlation 결과값이 일정 기준인 [TeX:] $$C_{P S S, t h}$$을 초과하면서 검출된 [TeX:] $$N_{I D}^{(2)}$$와 다른 PSS 수열인 조건으로 판단한다. 이후, 기존과 동일하게 PSS를 포함하는 수신 OFDM 심볼에 대해 FFT 과정을 거친 후 zero-forcing 기반으로 채널을 추정한다.
이후의 SSS 검출 단계에서 추정 채널을 사용하여 equalization 과정을 거쳐 보상된 수신 SSS 심볼을 획득한다. 이를 바탕으로 cross-correlation을 진행하면서 i번째 SSS 수열에 대한 correlation인 [TeX:] $$C_{1, i}^{\prime}$$ 값을 계산한다. 그리고 앞에서 간섭 신호가 존재하는 것으로 판단한 경우 equalization을 하지 않은 수신 SSS 심볼과 i번째 SSS 수열 간의 correlation인 [TeX:] $$C_{2, i}^{\prime}$$을 계산하고 [TeX:] $$C_{1, i}^{\prime} \text{와 } C_{2, i}^{\prime}$$을 비교하여 더 큰 값을 최종 correlation 결과인 [TeX:] $$C_{S S S, i}$$로 채택한다. 그리고 [TeX:] $$C_{S S S, i}$$ 값이 최대가 되는 SSS 수열 번호를 [TeX:] $$N_{I D}^{(1)}$$로 도출한다.
제안 기법은 앞의 수학 모델에서 관찰된 간섭의 영향을 감소시키는 방향으로 적응적인 SSS 검출을 수행한다. 앞의 수학 모델은 간섭 신호가 일정 수준 이상인 경우 추정 채널에 오차가 다소 발생하며, 이로 인해 채널 보상의 성능이 오히려 열화되는 것을 시사한다. 이에 착안하여 제안 기법은 간섭의 유무에 따라 equalization의 적용 여부를 적응적으로 결정한다. 그리고 equalization 적용 여부에 따른 두 가지 수신 심볼에 대한 correlation 결과를 확률적인 equalization 성능에 대한 수학적 분석을 기반으로 선택적으로 취함으로써 간섭의 영향을 최소화하고 간섭으로 인한 성능 열화를 효과적으로 방지한다. 또한, 간섭 환경에 따라 적응적으로 equalization을 진행하는 부분은 불필요한 연산의 부담을 줄이면서 계산 효율성을 높일 수 있다. 무엇보다 제안 기법은 LTE와 5G 두 시스템에 공통적으로 적용될 수 있는 장점을 가진다.
Ⅳ. SSS 검출 성능 검증
소프트웨어 모뎀에 그림 4의 알고리즘을 적용하여 Universal Software Radio Peripheral(USRP) 시스템을 사용한 테스트베드 시스템을 구성하였다. 우선 기본적인 제안 기법의 성능 관찰을 위해서 그림 5와 같이 emulated Next Generation Node B(gNB) 환경에서 실험을 진행하였다. gNB PC와 연결된 USRP의 Transmitter(TX) 포트와 UE PC와 연결된 USRP의 Receiver(RX) 포트를 Radio Frequency(RF) 케이블로 연결하여 AWGN 채널 환경을 구성하였다. 그리고 신호 감쇄기를 사용하여 수신 전 송신된 RF 신호를 감쇄시킴으로써, SNR을 조절하는 형태로 수신 신호 환경에 변화를 주었다. 그리고 gNB 및 UE PC에서는 연결된 USRP와 연동되어 기저대역 수준에서의 5G 기지국 신호 생성 및 UE 신호 처리를 수행하는 모뎀 소프트웨어가 구동되도록 하였다.
gNB 측 기저대역 소프트웨어는 Open Air Interface의 5G 오픈소스 코드를 활용하였다. 본 실험 환경에서 간섭 신호를 효과적으로 생성하기 위해 gNB 소프트웨어에서 두 가지 기지국 신호를 동시에 생성하면서, 각 기지국 신호의 기저대역 수준 전력 크기를 조절할 수 있도록 하였다. 테스트베드의 주요 파라미터는 5G 표준에 준하도록 표 1과 같이 설정하였다. 5G DL에서 사용되는 preamble sequence인 M-sequence를 PSS 수열로 가정하였으며, [TeX:] $$L_S$$ 및 l은 TS 38.211에 명시된 대로 각각 336 및 127로 설정하였다. 그리고 표준 문서에 따라 Bandwidth는 20MHz로 설정하였고, SCS (Subcarrier Spacing)은 30kHz, FFT size는 1024로 설정하였으며 샘플링 주기는 nyquist 정리에 따라 30.72MHz로 설정하였다. 서빙 기지국의 cell ID와 간섭 기지국의 cell ID는 각각 312 및 95로 설정하여 실험을 진행하였다. gNB PC에서 생성된 기지국 신호들은 gNB 측 USRP를 통해 RF 신호로 송신되고 단말기 측 USRP을 통해 수신 및 샘플링된다. 그리고 제안 기법이 구현된 UE 소프트웨어에서 수신된 기저대역 신호를 통해 cell search를 수행한다. 이러한 cell search 시도를 1000회 수준으로 반복하여 매 시도마다 검출되는 cell ID에 대한 성공률을 측정한다. 이와 같은 반복 실험을 다양한 간섭 신호의 세기에 대해 반복하면서 제안 기법의 cell ID 검출 성능을 평가하였다. 간섭 신호의 세기는 서빙 기지국 신호 대비 비율로 기저대역 신호의 세기를 조절하는 형태로 진행하였고, [TeX:] $$C_{P S S, t h}$$ 값은 간섭 신호가 존재하는 환경에서 간섭 신호와 서빙 기지국 신호 간의 최소한의 비율로 설정하였다.
표(Table) 1.
| FFT size | 1024 |
| Center frequency | 3.3GHz |
| Preamble sequence | M-sequence (5G) |
| Subcarrier spacing | 30kHz |
| Sampling rate | 30.72MHz |
| Bandwidth | 20MHz |
| CPU | Intel Core i7-8700K |
| Software defined radio | USRP B210 |
| [TeX:] $$L_S$$ | 336 |
| l | 127 |
| [TeX:] $$\omega$$ | 4 |
| [TeX:] $$C_{p s s, t h}$$ | 0.75 |
| Cell ID | 312(서빙), 95(간섭) |
4.1 제안 기법의 기능 검증
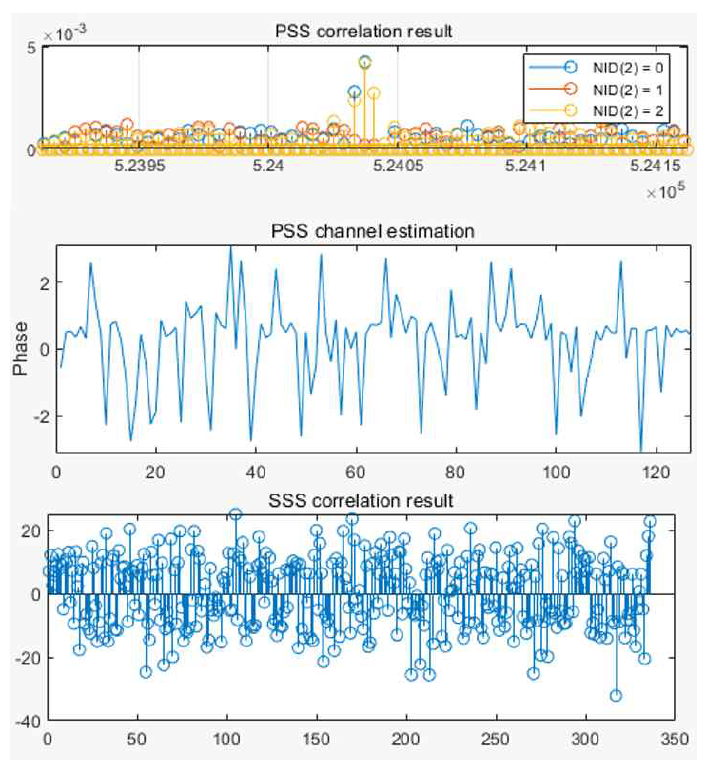
우선 간섭 기지국의 신호 세기를 서빙 기지국 신호 세기의 0.95배로 설정하여 cell search 시도를 하였을 때 제안기법의 기능 동작과정을 확인하였다. 그림 6은 PSS correlation 결과와 기존 기법으로 도출된 PSS 기반으로 추정된 채널의 위상 및 SSS correlation 결과를 나타내고 있다. PSS correlation 결과 그래프에서 서빙 및 간섭 기지국의 [TeX:] $$N_{I D}^{(2)}$$인 0 및 2에 대한 peak가 관찰되는 것이 보이는데, 이는 간섭 신호의 존재를 인지하는 제안 기법이 유효함을 보여주고 있다. 그리고 현재 실험 채널이 fading이 없는 것을 감안할 때, 추정된 채널이 간섭 신호에 의해 위상의 왜곡이 이루어진 것을 유추할 수 있다. 따라서 기존 기법이 이러한 채널 추정값으로 equalization 과정을 거치면서 그림 6 하단의 그래프처럼 SSS correlation 결과가 뚜렷한 peak를 얻지 못하는 것을 볼 수 있다. 이로 인해 기존 기법은 잘못된 SSS 검출을 통해 cell ID를 948로 잘못 획득하는 것을 관찰할 수 있다. 이와는 반대로, 그림 7은 동일한 수신 신호에 대해 제안 기법으로 얻은 SSS correlation 결과를 나타내고 있다. 기존 기법과는 다르게 간섭 신호를 인지하여 equalization을 거치지 않고 진행하여 상대적으로 [TeX:] $$N_{I D}^{(1)}$$ 값이 104인 peak가 뚜렷한 SSS correlation 결과를 얻게 된다. 결과적으로 제안 기법은 cell ID를 312로 검출하면서 간섭 환경에 적응적으로 동작하는 것을 볼 수 있다.
4.2 제안 기법의 수신 신호 세기 별 검출 성능 검증
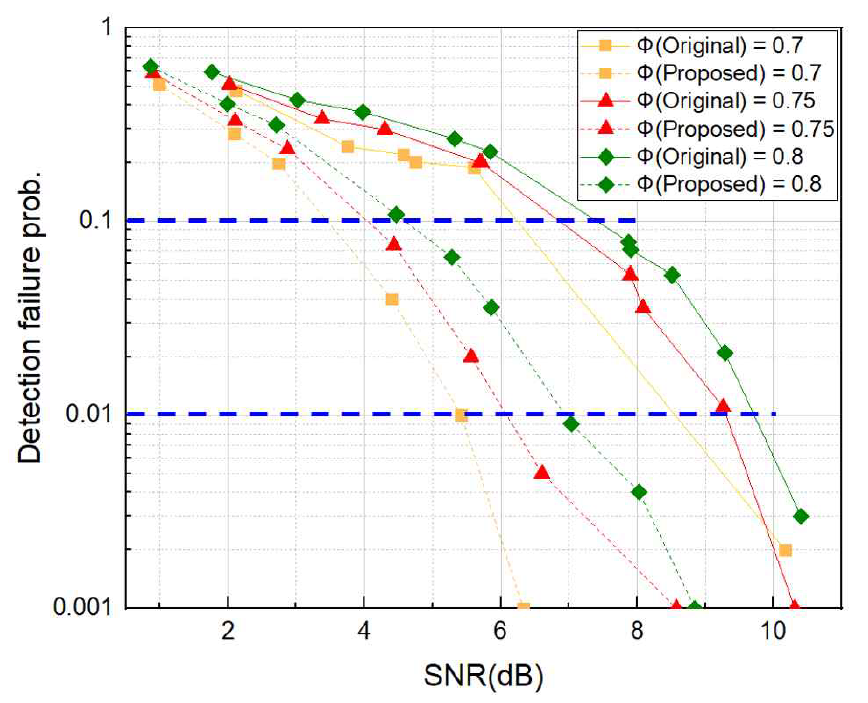
그림 8 및 9는 다양한 수신 신호 환경 및 간섭 신호 세기 환경에 대해 제안 기법과 기존 기법의 cell ID 검출 성능을 비교하여 나타내고 있다. 서빙 신호 대비 간섭 신호 세기 비율을 [TeX:] $$\Phi$$라고 정의할 때, [TeX:] $$\Phi$$가 0.7 - 1인 경우의 cell ID 검출 실패율 10%를 달성하기 위한 최소 SNR은 6.2 - 10.8dB인 반면, 제안 기법을 적용했을 때는 3.5 - 9.3dB로 나타났다. 따라서 이 성능 관점에서 제안 기법 적용을 통해 1.5 - 3dB의 SNR 이득을 얻는 것을 확인할 수 있다. 이를 통해 cell ID 검출 실패가 빈번한 약전계 환경에서 제안 기법이 뚜렷한 성능 개선 효과를 보이는 것을 알 수 있다. 또한 간섭 신호가 상대적으로 높은 환경에서 제안 기법의 성능 개선량이 비교적 작아지는 것을 볼 수 있다. 이는 간섭 신호가 서빙 신호와 유사한 세기일 때보다는 [TeX:] $$\Phi$$가 0.7-0.8 정도의 적절한 세기일 때 제안 기법이 더욱 효과적인 것을 암시한다.
그림(Fig.) 8.
그림(Fig.) 9.
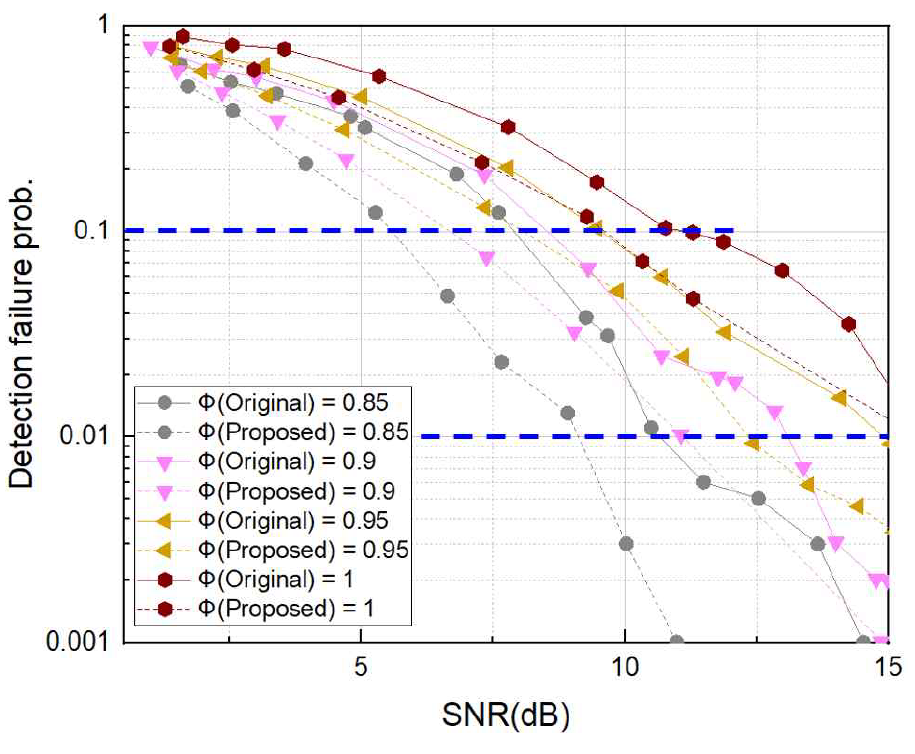
또한 cell ID 검출 실패율 1% 관점에서 보면, 기존 기법의 경우 이를 달성하기 위한 최소 SNR은 8.5 - 14.8dB인 반면, 제안 기법의경우 5.4 - 12 dB로 나타난다. 이를 통해 제안 기법이 1.6 - 3.3dB의 SNR gain을 가져오는 것을 확인할 수 있다. 이는 제안 기법이 cell ID를 수월하게 검출하는 강전계 환경에서도 약전계 환경에서와 유사한 성능 이득을 가져오는 것을 뜻한다. 즉, 제안 기법은 신호 환경에 영향을 받지 않고 비교적 일정한 성능 이득을 가져오는 것을 확인할 수 있다. 또한, 이 관점에서도 간섭 신호의 세기가 강할 때 제안 기법의 성능 개선량이 감소하는 것을 볼 수 있다. 이는 간섭 신호의 영향력 강화로 인해 equalization 여부와 관계없이 SSS 검출이 부정확해지는 것이 원인이라 볼 수 있다. 따라서 제안 기법은 간섭 신호의 세기에 따라 그 성능 이득이 좌우되는 것을 확인할 수 있다.
4.3 제안 기법의 복잡도 성능
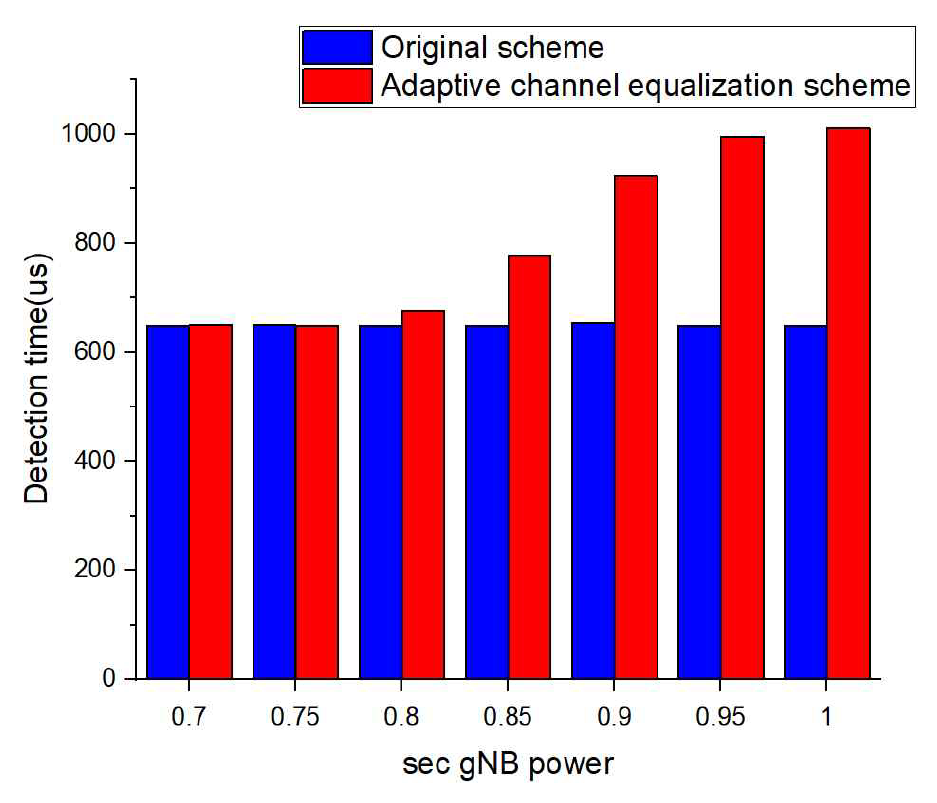
그림 10은 간섭 신호 세기에 따라 기존 및 제안 기법의 SSS 검출 소요 시간을 비교한 것이다. 기존 기법은 간섭 신호의 세기와 무관하게 SSS 검출의 소요 시간이 일정한 반면, 제안 기법은 간섭 신호의 세기가 커짐에 따라 SSS 검출의 소요 시간이 증가하는 것을 확인할 수 있다. 이는 간섭 신호의 세기가 클수록 제안 기법의 알고리즘 19-20번째 줄로 인해 간섭 신호를 인식하는 빈도가 증가하게 되고, 이로 인한 추가적 correlation 계산이 발생하기 때문이다. 간섭 신호 세기가 0.7일 때는 SSS 검출의 소요 시간이 [TeX:] $$0.4 \mu \mathrm{s}$$ 수준 증가하고 간섭 신호 세기가 0.8 - 1.0일 때 각각 [TeX:] $$29-363 \mu \mathrm{s},$$ 수준으로 더 길게 나타났다. 다만 전체 cell 탐색 시간이 수십-수백ms 임을 감안할 때, 제안 기법으로 인한 추가 소요 시간은 무시할만한 수준이라 볼 수 있다. 즉, 전체 cell 탐색 관점에서는 기존 기법과 제안 기법이 비슷한 수준이라 결론지을 수 있다. 이를 통해 적응적인 SSS 채널 보상 기법에서 추가적인 correlation 계산 과정이 필요하더라도 cell 탐색 시간에 큰 영향을 미치지 않으면서 cell search의 성능 개선을 가져온다고 볼 수 있다.
그림(Fig.) 10.
4.4 상용 시나리오에서의 제안 기법의 효용성 검증
추가로 상용 시나리오에서 제안 기법의 효용성을 확인하기 위해서 상용 신호를 대상으로 4.2 실험을 반복하였다. 그림 11에 나타난 바와 같이 노트북 형태의 UE PC를 활용하고 이와 연결된 USRP의 RX 포트 안테나를 통해 수신된 상용 신호를 실시간으로 처리하면서 제안 기법의 성능을 관찰하였다. 또한 건물 밀도가 높은 도심 환경 속 간섭 신호 환경에 해당하는 그림 11의 고정점에서 실험을 진행하였다. 표 1과 대부분의 세부 실험 파라미터가 동일하면서 중심주파수는 KT 상용망에서 활용하는 3.55GHz로 설정하고 multi-path fading이 존재하는 무선 채널 환경에서 실험을 진행하였다.
그림 12는 상용 환경에서 간섭 기지국의 신호 세기에 대해 제안된 적응적 SSS 채널 보상 기법의 성능을 나타낸 그래프로, 상용 시나리오에서 기존 및 제안기법의 cell ID 검출 성능을 비교한 것이다. 기존 기법과 제안 기법의 cell ID 검출 성공률은 각각 86.2% 및 98.6%로 측정되었으며, 이때 두 경우의 최소 SNR 값은 14.6dB로 나타났다.
그림(Fig.) 12.
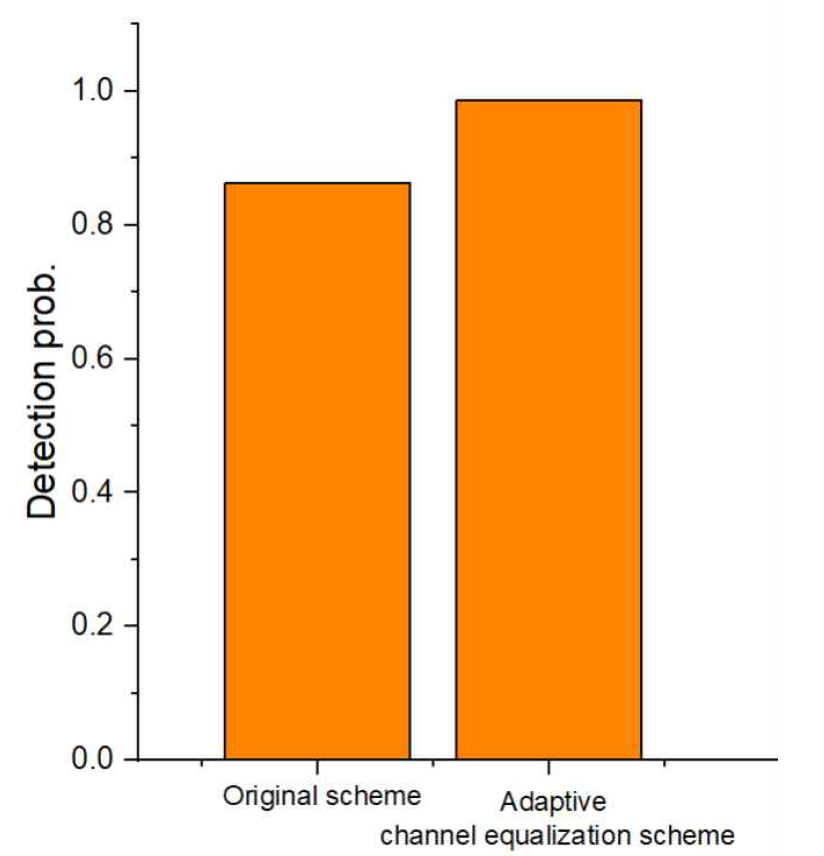
또한, 제안 기법으로 인해 약 12.4% 성공률 수준의 cell 탐색 성능이 향상되는 결과를 얻었다. 따라서 UE가 특정 고정점에 머무르는 상황에서 제안 기법이 간섭 효과를 잘 억제하고 사용자가 체감 가능한 수준의 성능 개선을 이루는 것을 확인할 수 있다. 결론적으로 본 상용 시나리오 기반 실험을 통해 상용 신호를 바탕으로 간섭 환경에서 제안 기법이 더 높은 신뢰성의 cell 탐색이 가능한 것을 확인할 수 있었다. 이는 특히 간섭 환경이 빈번한 도심지에서 제안 기법이 실제 사용자에게 안정적인 cell 탐색으로 인한 네트워크 접속성을 보장하는데 기여할 수 있음을 유추할 수 있다.
Ⅴ. 결 론
본 논문에서는 여러 기지국의 신호가 존재하는 상황에서 효과적으로 cell ID를 탐색하기 위해 적응적인 equalization 기법을 제안하였다. 기존 방식에서 SSS 검출 전에 equalization을 진행하는 과정 중, 채널 간섭이 주는 영향을 수학적으로 분석하였다. 이를 바탕으로 간섭 신호가 탐색 되었을 때 equalization을 진행하지 않는 adaptive equalization 기법을 제안하였다. 그리고 제안 기법의 알고리즘을 하드웨어 테스트베드로 구현하여 실험을 통해 간섭 신호 환경에서도 신뢰성 높은 결과를 도출할 수 있는 성능을 입증하였다. 또한, 상용 신호를 통한 실험으로 기존 기법보다 향상된 성능을 입증하며 제안 기법의 상용화 가능성도 확인하였다. 이는 LTE와 5G의 공통적인 문제를 동시에 해결하며 효율적으로 두 시스템에 적용될 수 있음을 시사한다. 따라서 본 연구는 간섭 신호 환경에서도 효율적이고 신뢰성 높은 cell 탐색을 가능하게 하여 차세대 통신 시스템 발전에 기여할 것으로 기대한다.
Biography
Biography
References
- 1 A. Ghosh, A. Maeder, M. Baker, and D. Chandramouli, "5G evolution: A view on 5G cellular technology beyond 3GPP Release 15," in IEEE Access, vol. 7, pp. 127639-127651, 2019.custom:[[[-]]]
- 2 Y. Tsai, G. Zhang, D. Grieco, F. Ozluturk, and X. Wang, "Cell search in 3GPP long term evolution systems," in IEEE Veh. Technol. Mag., vol. 2, no. 2, pp. 23-29, Jun. 2007. (https://doi.org/10.1109/mvt.2007.912929)doi:[[[10.1109/mvt.2007.912929]]]
- 3 R. D'Avella, L. Moreno, and M. Sant'Agostino, "Adaptive equalization in TDMA mobile radio systems," 37th IEEE Veh. Technol. Conf., pp. 385-392, Tampa, FL, USA, 1987. 그림 11. 상용신호실험환경및구축 Fig.11. Commercial signal experimental environment and setup 그림 12. 상용신호 SSS검출성공률측정결과 Fig.12. Measurement results of SSS detection success rate for commercial signals 1055 (https://doi.org/10.1109/vtc.1987.1623574)doi:[[[10.1109/vtc.1987.1623574]]]
- 4 P. Monsen, "MMSE equalization of interference on fading diversity channels," in IEEE Trans. Commun., vol. 32, no. 1, pp. 5-12, Jan. 1984. (https://doi.org/10.1109/tcom.1984.1095956)doi:[[[10.1109/tcom.1984.1095956]]]
- 5 R. W. Lucky, "Techniques for adaptive equalization of digital communication systems," in The Bell Syst. Tech. J., vol. 45, no. 2, pp. 255-286, Feb. 1966. (https://doi.org/10.1002/j.1538-7305.1966.tb000 20.x)doi:[[[10.1002/j.1538-7305.1966.tb00020.x]]]
- 6 Y.-H. You and H. -K. Song, "Effective joint detection of synchronization signal, duplex mode, and frequency offset for LTE machinetype communications," in IEEE Internet of Things J., vol. 7, no. 11, pp. 10922-10931, Nov. 2020. (https://doi.org/10.1109/jiot.2020.2993492)doi:[[[10.1109/jiot.2020.2993492]]]
- 7 C. E. M. Silva, G. J. Dolecek, and F. J. Harris, "Cell search in long term evolution systems: Primary and secondary synchronization," 2012 IEEE 3rd LASCAS, pp. 1-4, Playa del Carmen, Mexico, 2012. (https://doi.org/10.1109/lascas.2012.6180345)doi:[[[10.1109/lascas.2012.6180345]]]
- 8 K. Manolakis, D. M. Gutierrez Estevez, V. Jungnickel, W. Xu, and C. Drewes, "A closed concept for synchronization and cell search in 3GPP LTE systems," 2009 IEEE Wireless Commun. and Netw. Conf., pp. 1-6, Budapest, Hungary, 2009. (https://doi.org/10.1109/wcnc.2009.4917491)doi:[[[10.1109/wcnc.2009.4917491]]]
- 9 S. Yoneda, M. Sawahashi and S. Nagata, "Initial physical cell ID detection time using NR synchronization signals based on systemlevel simulation," 2022 IEEE 33rd Annual Int. Symp. PIMRC, pp. 616-621, Kyoto, Japan, 2022. (https://doi.org/10.1109/pimrc54779.2022.9977 661)doi:[[[10.1109/pimrc54779.2022.9977661]]]
- 10 D. Inoue, K. Ota, M. Sawahashi, and S. Nagata, "Physical cell ID detection using joint estimation of frequency offset and SSS sequence for NR initial access," 2021 IEEE 93rd VTC2021-Spring, pp. 1-6, Helsinki, Finland, 2021. (https://doi.org/10.1109/vtc2021-spring51267.2 021.9448662)doi:[[[10.1109/vtc2021-spring51267.2021.9448662]]]
- 11 I. Kim, Y. Han, Y. Kim, and S. C. Bang, "Sequence hopping cell search scheme for OFDM cellular systems," in IEEE Trans. Wireless Commun., vol. 7, no. 5, pp. 14831489, May 2008. (https://doi.org/10.1109/twc.2008.060992)doi:[[[10.1109/twc.2008.060992]]]
- 12 S. Nagata, Y. Kishiyama, M. Tanno, K. Higuchi, and M. Sawahashi, "Cell search time comparison using hierarchical and nonhierarchical synchronization channels in OFDM based evolved UTRA downlink," 2007 IEEE 65th VTC2007- Spring, pp. 1239-1244, Dublin, Ireland, 2007. (https://doi.org/10.1109vetecs.2007.261)doi:[[[10.1109vetecs.2007.261]]]
- 13 J.-I. Kim, J.-S. Han, H.-J. Roh, and H.-J. Choi, "SSS detection method for initial cell search in 3GPP LTE FDD/TDD dual mode receiver," 2009 9th Int. Symp. Commun. and Inf. Technol., pp. 199-203, Icheon, Korea, 2009. (https://doi.org/10.1109/iscit.2009.5341260)doi:[[[10.1109/iscit.2009.5341260]]]
- 14 B. Li, G. Sun, and X. Wang, "SSS detection scheme for neighbor cell search in 3GPP LTE systems," 2011 IEEE GLOBECOM 2011, pp. 1-5, Houston, TX, USA, 2011. (https://doi.org/10.1109/glocom.2011.6133513)doi:[[[10.1109/glocom.2011.6133513]]]
- 15 Z. Yan, G. Sun, and X. Wang, "A novel initial cell search scheme in TD-LTE," 2011 IEEE 73rd VTC Spring, pp. 1-5, Budapest, Hungary, 2011. (https://doi.org/10.1109/vetecs.2011.5956122)doi:[[[10.1109/vetecs.2011.5956122]]]
- 16 J. Myung, J. Kang, Y. Baek, and B. Koo, "Efficient S-SCH detection algorithm for LTE downlink channel," in IEEE Trans. Veh. Technol., vol. 63, no. 6, pp. 2969-2973, Jul. 2014. (https://doi.org/10.1109/tvt.2013.2295093)doi:[[[10.1109/tvt.2013.2295093]]]
- 17 M. Morelli and M. Moretti, "A maximum likelihood approach for SSS detection in LTE systems," in IEEE Trans. Wireless Commun., vol. 16, no. 4, pp. 2423-2433, Apr. 2017. (https://doi.org/10.1109/twc.2017.2664835) 1056doi:[[[10.1109/twc.2017.2664835]]]
- 18 Y.-H. You, J.-H. Park, and I.-Y. Ahn, "Complexity effective sequential detection of secondary synchronization signal for 5G new radio communication systems," in IEEE Syst. J., vol. 15, no. 3, pp. 3382-3390, Sep. 2021. (https://doi.org/10.1109/jsyst.2020.3001925)doi:[[[10.1109/jsyst.2020.3001925]]]
- 19 I. Kim, Y. Han, and H. K. Chung, "An efficient synchronization signal structure for OFDM-based cellular systems," in IEEE Trans. Wireless Commun., vol. 9, no. 1, pp. 99-105, Jan. 2010. (https://doi.org/10.1109.twc.2010.01.090516)doi:[[[10.1109.twc.2010.01.090516]]]
- 20 F. Wang, Y. Zhu, and Z. Wang, "A low complexity scheme for S-SCH detection in 3GPP LTE downlink system," 2010 Global Mobile Congress, pp. 1-6, Shanghai, China, 2010. (https://doi.org/10.1109/gmc.2010.5634613)doi:[[[10.1109/gmc.2010.5634613]]]
- 21 Y. Tsuchida, S. Nagata, and M. Sawahashi, "Cell search time performance using multipath signals in LTE downlink," 2011 IEEE 73rd VTC Spring, pp. 1-5, Budapest, Hungary, 2011. (https://doi.org/10.1109/vetecs.2011.5956774)doi:[[[10.1109/vetecs.2011.5956774]]]
- 22 J. G. Andrews, W. Choi, and R. W. Heath, "Overcoming interference in spatial multiplexing MIMO cellular networks," in IEEE Wireless Commun., vol. 14, no. 6, pp. 95-104, Dec. 2007. (https://doi.org/10.1109/mwc.2007.4407232)doi:[[[10.1109/mwc.2007.4407232]]]
- 23 J. G. Andrews, "Interference cancellation for cellular systems: A contemporary overview," in IEEE Wireless Commun., vol. 12, no. 2, pp. 19-29, Apr. 2005. (https://doi.org/10.1109/mwc.2005.1421925)doi:[[[10.1109/mwc.2005.1421925]]]
- 24 Y.-C. Liu, K.-C. Lin, and Y. T. Su, "Initial synchronization for multi-cell OFDMA systems," 2009 IEEE Int. Conf. Commun., pp. 1-5, Dresden, Germany, 2009. (https://doi.org/10.1109/icc.2009.5199084)doi:[[[10.1109/icc.2009.5199084]]]
- 25 J.-W. Lee and Y.-H. Lee, "Resource allocation for OCI reduction in OFDM-based asynchronous cellular systems," 2007 IEEE 65th VTC2007-Spring, pp. 1941-1945, Dublin, Ireland, 2007. (https://doi.org/10.1109/vetecs.2007.402)doi:[[[10.1109/vetecs.2007.402]]]
- 26 S. S. Khalifa, H. S. Hamza, and K. Elsayed, "Self-adaptive inter-cell interference coordination scheme for LTE systems," 2013 IEEE 24th Annual Int. Symp. PIMRC, pp. 1779-1783, London, 2013. (https://doi.org/10.1109/pimrc.2013.6666431)doi:[[[10.1109/pimrc.2013.6666431]]]
- 27 C. Li, J. Zhang, M. Haenggi, and K. B. Letaief, "User-centric intercell interference nulling for downlink small cell networks," in IEEE Trans. Commun., vol. 63, no. 4, pp. 1419-1431, 2015. (https://doi.org/10.1109/tcomm.2015.2402121)doi:[[[10.1109/tcomm.2015.2402121]]]
- 28 Z. Li, J. Tong, Y. Ma, X. Li, D. Yang, and Y. Lei, "Timing and frequency synchronization using ZCZ sequences for multi-cell OFDM systems," 2017 3rd IEEE ICCC, pp. 6-11, Chengdu, China, 2017. (https://doi.org/10.1109/compcomm.2017.8322 505)doi:[[[10.1109/compcomm.2017.8322505]]]
- 29 Y. Ryu and J. G. Kim, "Cell search for 3GPP LTE system using interference cancellation," 2015 Seventh Int. Conf. Ubiquitous and Future Netw., pp. 579-584, Sapporo, 2015. (https://doi.org/10.1109/icufn.2015.7182610)doi:[[[10.1109/icufn.2015.7182610]]]
- 30 R. Peng, Y. Tian, and S. Han, "ICI-free channel estimation and wireless gesture recognition based on cellular signals," in IEEE Wireless Commun. Lett., vol. 12, no. 12, pp. 2088-2092, Dec. 2023. (https://doi.org/10.1109/lwc.2023.3307621)doi:[[[10.1109/lwc.2023.3307621]]]
- 31 W. Li, Y. Zhang, L.-K. Huang, J. Cosmas, and Q. Ni, "A cell specific reference signal interference cancellation scheme for LTE cellular access systems," 2015 IEEE Int. Symp. Broadband Multimedia Syst. and Broadcasting, pp. 1-6, Ghent, Belgium, 2015. (https://doi.org/10.1109/bmsb.2015.7177212)doi:[[[10.1109/bmsb.2015.7177212]]]
- 32 A. G. Wassal and A. R. Elsherif, "Efficient implementation of secondary synchronization symbol detection in 3GPP LTE," 2011 IEEE ISCAS, pp. 1680-1683, Rio de Janeiro, Brazil, 2011. (https://doi.org/10.1109/iscas.2011.5937904)doi:[[[10.1109/iscas.2011.5937904]]]
- 33 P. Wang and F. Berggren, "Secondary 1057 synchronization signal in 5G new radio," 2018 IEEE ICC, pp. 1-6, Kansas City, MO, USA, 2018. (https://doi.org/10.1109/icc.2018.8422145)doi:[[[10.1109/icc.2018.8422145]]]
- 34 A. Omri, M. Shaqfeh, A. Ali, and H. Alnuweiri, "Synchronization procedure in 5G NR systems," in IEEE Access, vol. 7, pp. 41286-41295, 2019. (https://doi.org/10.1109/access.2019.2907970)doi:[[[10.1109/access.2019.2907970]]]
- 35 K.-C. Shin, S.-B. Im, K.-M. Ok, and H.-J. Choi, "A design of initial cell searcher for 3GPP LTE downlink system," J. KICS, vol. 33, no. 7, pp. 733-742, Jul. 2008. (G704-A00600.2008.33.7.005)custom:[[[-]]]
- 36 3GPP TS 38.211 v17.0.0 (2024).custom:[[[-]]]
- 37 3GPP TS 36.211 v17.0.0 (2024).custom:[[[-]]]