Heonwoo Chu , Taehan Moon , Tae-Yoon Kim , Hanjin Jeong , Yongmin Song and Jae-Hyun Kim
Handover Optimization Method for Cross-Seam in LEO Satellite Basedon Orbital Information
Abstract: In the cross-seam of a LEO (low Earth orbit) satellite network, when a handover occurs between satellites in adjacent orbits, the absence of inter-plane ISLs (inter-satellite links) can lead to increased handover interruption time and routing instability. In this paper, we propose a method to reduce handover interruption time and routing instability in LEOsatellite network in cross-seam regions, where ISLs between adjacent orbits are unavailable. The proposedhandover method calculates thecentral longitude of the cross-seamusing satellite orbital information and conducts handovers based on this longitude, minimizing changes in the orbits of the previously connected and newly connected satellites during cross-seam handover. Simulation results show that the proposed handover method reduces handover interruption time in the cross-seam.
Keywords: LEO Satellite Network , Handover , Walker-Star Constellation
Ⅰ. 서 론
저궤도(low Earth orbit, LEO) 위성 네트워크는 광범위한 커버리지와 짧은 지연시간으로 지구 전역에 통신 서비스를 제공할 수 있어 6G 통신 구현에 필수적인 요소로 주목받고 있다. 그러나, 저궤도 위성은 약 7.8 km/s의 빠른 속도로 공전하므로, 단일 위성으로는 특정지역에 대한 지속적인 서비스가 불가능하다. 따라서, 하나의 위성이 서비스를 종료하기 전에 다음 위성이 동일 지역을 커버해야 하며, 핸드오버 과정에서의 서비스 단절을 최소화하기 위해 다수의 저궤도 위성이 필요하다[1].
상용 저궤도 위성 네트워크에서는 워커(Walker) 방식의 배치를 보편적으로 사용한다. 워커 방식의 배치는 워커-델타(Walker-Delta)와 워커-스타(Walker-Star) 두 가지로 분류된다[2]. 워커-델타 방식에서는 저궤도 위성의 궤도가 0에서 2π 사이의 값을 균등한 간격으로하여 승교점 적경(Right Ascension of Ascending Node, RAAN) 값을 갖는다. 반면, 워커-스타 방식에서는 저궤도 위성의 궤도가 0에서 π 사이의 값을 균등한 간격으로 하여 승교점 적경 값을 갖는다. 워커-스타 방식은 일반적으로 [TeX:] $$90^{\circ}$$에 가까운 궤도 경사각을 가지며, 지구 전역에 통신 서비스 제공이 가능하다. 워커-스타의 저궤도 위성 배치를 사용하는 상용 저궤도 위성 네트워크에는 OneWeb, Iridium 등이 있다[3,4].
저궤도 위성은 위성 간 링크(inter-satellite link, ISL)를 통해 네트워크를 형성한다. ISL에는 동일 궤도 간 ISL(intra-plane ISL)과 인접 궤도 간 ISL(inter-plane ISL)이 있다. 동일 궤도 간 ISL로 연결된 두 위성은 상대 속도 및 위치 변화가 적어 ISL이 안정적으로 유지될 수 있다. 반면, 인접 궤도 간 ISL로 연결된 두 위성은 상대 속도 및 위치 변화가 크고, 다른 궤도의 위성으로부터의 간섭이 증가하여 링크 단절(link failure)이 발생할 수 있다.
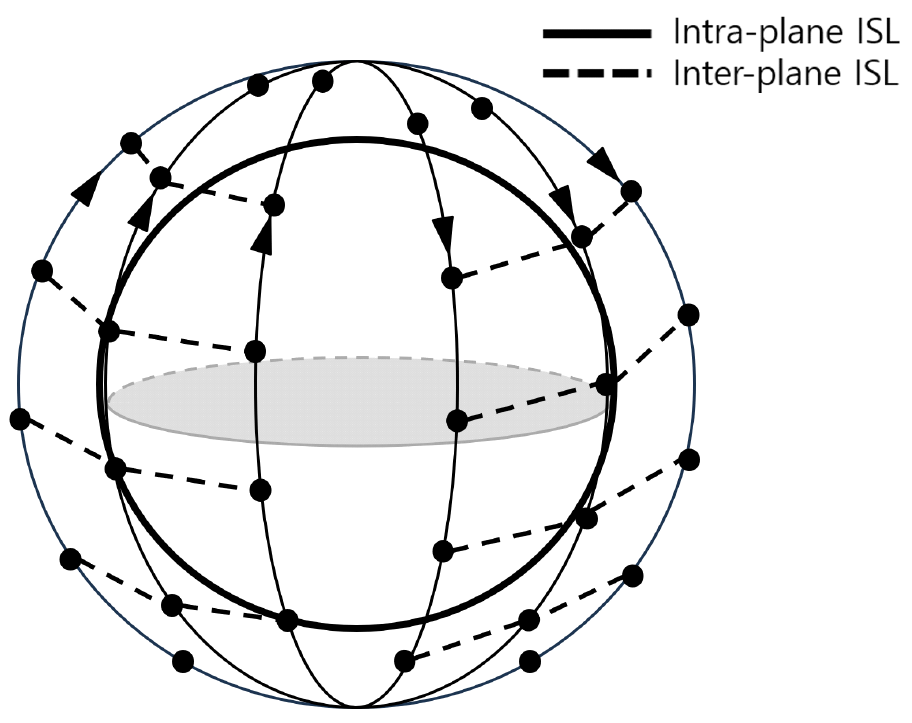
워커-스타 방식의 저궤도 위성 배치에서는 그림 1과 같이 궤도 간 위성 링크 단절 구간(cross-seam)과 극지역 통신 제한 구간(polar region) 존재한다. Cross-seam은 인접한 두 궤도의 위성이 반대 방향으로 이동하여 큰 상대 속도로 인해 인접 궤도 간 ISL 형성이 불가능하다. Cross-seam은 지구 중심을 기준으로 대칭된 두 영역에 형성되며, 지구의 자전에 따라 위치가 변한다. 한편, 극지역 통신 제한 구간은 위성 궤도가 교차하는 극점을 중심으로 형성되며, 이지역에서는 궤도 간거리가 좁아짐에 따라 인접한 궤도의 위성 간 거리가 감소한다. 위성 간 거리가 감소함에 따라 상대 속도 및 간섭이 증가하여 극지역 통신 제한 구간에서는 인접 궤도 간 ISL 형성이 불가능하다[5,6].
그림(Fig.) 1.
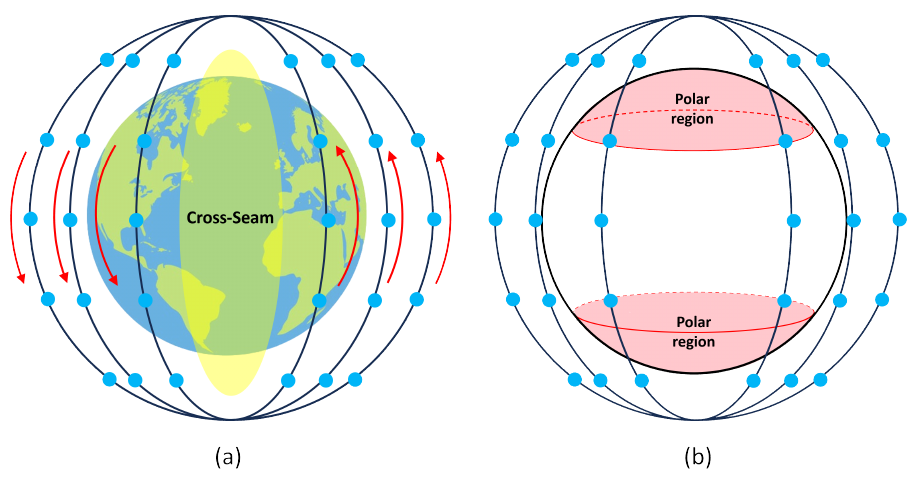
Cross-seam에 인접한 두 궤도의 위성 간 핸드오버가 발생할 경우, 큰 핸드오버 통신 중단시간(interruption time) 및 라우팅 경로에 큰 변화가 발생한다. Cross-seam에 인접한 두 궤도의 위성 사이에는 직접적인 ISL이 존재하지 않으므로, 극점을 통해 핸드오버를 수행해야 하며, 이 과정에서 핸드오버 통신 중단시간이 크게 발생한다. 또한, 지상국(ground station)과 연결된 저궤도 위성의 토폴로지 상 위치 변화가 커짐에 따라 라우팅 경로가 크게 변경된다.
[7]에서는 위치 기반 라우팅 알고리즘인 SAGRW(Seam-Aware Geographical Random Walk)를 제안하여 cross-seam 경계를 인식하는 방식으로 무작위 경로 선택과 부하 분산을 수행하였다. 그러나 핸드오버 통신 중단 시간이나 cross-seam에서 궤도 전환 관리와 같은 연결 연속성에 대한 분석은 포함하지 않았다.
[8]에서는 워커 모델을 기반으로 위성 세션 지속 시간(session duration)을 이론적으로 분석하고, 핸드오버 주기를 추정할 수 있는 모델을 제시하였다. 그러나 cross-seam으로 인한 핸드오버 실패 가능성이나 라우팅 경로의 불안정성 문제는 고려하지 않았다.
[9]에서는 워커-델타 궤도 기반 위성망에서의 성능 개선을 위해 inter-mesh 링크 스케줄링 기법을 제안하였으며, BMF(Bellman-Ford) 및 UCS(Uniform Cost Search) 기반의 경량화된 라우팅 구조를 적용하여 종단간 지연(E2E delay), 메모리 사용량, 전력 소모 등의 측면에서 성능 향상을 입증하였다. 하지만 inter-mesh ISL을 구성할 수 있는 워커-델타 구조에만 적용 가능하며, 워커-스타와 같이 구조적으로 인접 궤도 간 ISL 형성이 불가능한 cross-seam에서는 적용이 어렵다.
한편, [10]에서는 사용자 수요 기반의 핸드오버 최적화 전략을 통해 전체 핸드오버 횟수를 줄이는 방안을 제안하였다. 그러나 cross-seam에서의 연결 단절 문제를 고려하지 않았으며, 이에 따른 라우팅 경로의 불안정성에 대한 분석이 필요하다.
기존 연구들은 주기적으로 반복되는 cross-seam에서의 핸드오버 불균형 문제를 고려하지 않았으며, 이는 고위도에서 발생 빈도가 증가하는 cross-seam에서의 핸드오버에 의한 통신 중단시간 문제에 취약하다.
본 논문에서는 저궤도 위성의 궤도 정보를 활용하여 cross-seam에 인접한 두 궤도의 위성 간 핸드오버로 인해 발생하는 궤도 변경을 최소화함으로써 긴 핸드오버 통신 중단시간과 라우팅 경로 변화 발생을 줄이는 방안을 제안한다. 제안한 기법은 cross-seam 구간에서의 핸드오버 발생 횟수를 최소화하고, cross-seam 핸드오버 통신 중단 시간을 감소시키는 것을 확인하였다.
Ⅱ. 시스템 모델
본 논문에서는 워커-스타 방식으로 배치된 저궤도 위성 네트워크 환경을 가정한다. 위성 네트워크는 궤도 경사각 α를 갖는 [TeX:] $$N=\{n \mid n=1,2, \ldots, N\}$$개의 궤도로 구성되며 각 궤도에는 [TeX:] $$M=\{m \mid m=1,2, \ldots, M\}$$개의 위성이 배치된다. 저궤도 위성은 최소 고도각(minimum elevation angle, [TeX:] $$\theta_\min$$)을 만족하는 경우 지상국과 통신할 수 있으며, 시간 t에서 지상국과의 고도각을 [TeX:] $$\theta_{n, m}(t)$$로 나타낸다. 지상국에서는 최소 고도각을 만족하는 위성 중 가장 가까운 위성으로부터 서비스를 제공받는다.
각 위성은 그림 2와 같이 동일 궤도 내 인접한 2개의 위성과 동일 궤도 간 ISL을 형성하며, 인접 궤도 내 인접한 2개의 위성과 인접 궤도 간 ISL을 형성하여 총 4개의 ISL을 통해 위성 네트워크를 구성한다[11]. 그러나, cross-seam 및 극지역 통신 제한 구간에서는 인접 궤도 간 ISL 단절이 발생한다. 극지역 통신 제한 구간은 특정 위도를 기준으로 정의되며, 해당 위도보다 높은 위도에서는 인접 궤도 간 ISL에 단절이 발생한다[12].
네트워크의 지연은 전파 지연(propagation delay), 전송 지연(transmission delay), 노드 처리 지연(node processing delay), 큐잉 지연(queuing delay)으로 구성된다. 이 중 전송 지연과 노드 처리 지연은 위성의 성능에 크게 영향을 받으며, 큐잉 지연은 네트워크 트래픽 상태에 따라 변동될 수 있다. 따라서, 핸드오버로 인한 네트워크 성능 변화를 분석하기 위해, 본 논문에서는 전파 지연만을 고려한다. 따라서, 위성 네트워크에서의 지연(D)은 source에서 destination까지 K개의 ISL을 통해 통신이 이루어질 때 다음과 같이 정의한다.
k는 경로를 따라 연결된 ISL의 순서를 나타내며, [TeX:] $$L_k$$은 k번째 ISL의 길이를 의미한다. c는 빛의 속도를 나타낸다.
Ⅲ. Cross-seam 핸드오버로 인한 지연 및 경로 변경 문제
저궤도 위성을 활용한 위성 네트워크에서는 위성의 공전으로 인해 핸드오버가 빈번하게 발생한다. 또한, 지상국과 인접한 두 궤도 간 거리가 작은 경우, 두 궤도의 위성 간 핸드오버가 빈번하게 발생한다.
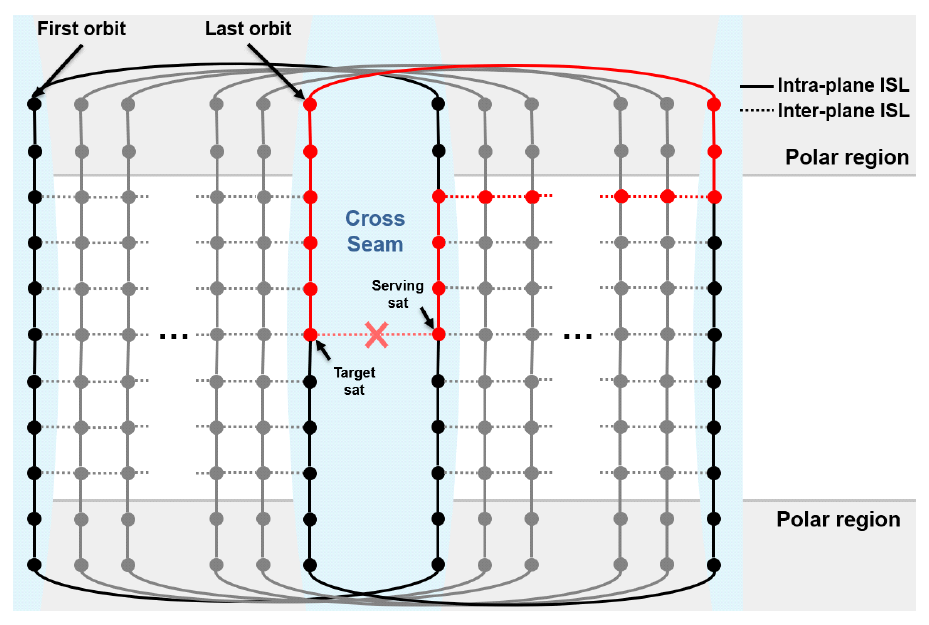
Cross-seam 핸드오버는 인접 궤도 간 ISL 단절로 인해 핸드오버 과정에서 다수의 인접 궤도 간 ISL 및 동일 궤도 간 ISL이 추가로 필요하게 된다. 예를 들어, 그림 3에서 빨간색으로 표시된 경로를 보면, 원래 인접 궤도 간 ISL 1개만으로 가능했던 핸드오버가 수십 개의 인접 궤도 간 ISL 및 동일 궤도 간 ISL을 경유해야 하는 상황이 발생한다. 이러한 추가적인 경로 설정은 핸드오버 지연 증가 및 네트워크 효율 저하를 초래한다. 특히, 위성의 토폴로지가 크게 변화하면서 라우팅 경로 설정에 영향을 미치며, 이에 따라 라우팅 테이블 관리의 복잡도가 증가한다. 또한, 네트워크 내에서 불규칙한 지연 변동(jitter)이 발생하여 데이터 전송의 안정성을 저하시킬 뿐만 아니라, 전체적인 네트워크 성능 저하를 유발한다. 따라서, cross-seam 핸드오버 문제를 효과적으로 해결할 수 있는 기법이 필요하며, 이를 위해 지연을 최소화하는 최적의 핸드오버 전략이 요구된다[7,13].
Ⅳ. 제안하는 Cross-seam 핸드오버 기법
본 논문에서는 cross-seam 핸드오버로 인한 지연 및 경로 변경 문제를 해결하는 기법을 제안한다. 제안하는 핸드오버 기법은 위성의 궤도 정보를 활용하여 불필요한 cross-seam 핸드오버를 최소화함으로써, 네트워크 성능 저하를 방지하고 핸드오버 지연을 줄이는 데 초점을 맞춘다.
제안하는 핸드오버 절차는 알고리즘 1과 같다. 먼저 지상국이 cross-seam에 있는지 확인해야 한다. Cross-seam은 그림 3과 같이 첫 번째 궤도와 마지막 궤도 사이에 있으므로, 첫 번째 궤도와 마지막 궤도에 속한 위성의 서비스 가능 여부를 확인하고, 지상국과 가장 가까운 위성이 두 궤도 중 하나에 속하는지 확인한다. 이를 판단하는 수식은 다음과 같이 정의한다.
(2)
[TeX:] $$b(t)=\left\{\begin{array}{lc} 1, & \text { if }\{1, N\} \subseteq P(t) \text { and } C(t) \in\{1, N\} \\ 0, & otherwise, \end{array}\right.$$P(t)는 시간 t에서 서비스가 가능한 위성들이 포함된 궤도의 집합을 의미하며 다음과 같이 정의한다.
C(t)는 시간 t에서 지상국과 가장 가까운 위성이 속한 궤도를 의미한다. b(t)는 시간 에서 지상국이 cross-seam에 위치하는지를 나타낸다. 만일 첫 번째 혹은 마지막 궤도가 P(t)에 포함되며, C(t)가 첫 번째 혹은 마지막 궤도인 경우, cross-seam에 속한다고 판단하여 b(t)를 1로 정의하고, 그 외의 경우에는 b(t)를 0으로 정의한다. 따라서, b(t)가 0인 경우 cross-seam을 고려하지 않고 가장 가까운 위성이 지상국에 서비스를 제공한다.
b(t)를 기반으로 지상국이 cross-seam에 존재한다고 판단되면, 제안하는 핸드오버를 수행하기 위해 첫번째와 마지막 궤도 중 지상국과 더 가까운 거리에 있는 궤도를 판단한다. 이를 위해 지상국의 위도([TeX:] $$\phi$$)에서 cross-seam의 중심 경도([TeX:] $$\lambda_{\text {cross }, \phi}(t)$$)를 계산하고, 지상국의 경도(λ)와 비교하여 지상국과 더 가까운 궤도에 존재하는 위성이 서비스를 제공한다. [TeX:] $$\lambda_{\text {cross }, \phi}(t)$$는 [TeX:] $$\phi$$에서의 첫 번째 궤도 경도[TeX:] $$\left(\lambda_{1, \phi}(t)\right), \phi$$에서의 마지막 궤도 경도[TeX:] $$\left(\lambda_{N, \phi}(t)\right)$$를 통해 계산되며, 계산식은 다음과 같다.
(4)
[TeX:] $$\begin{aligned} f & \left(\lambda_{1, \phi}(t), \lambda_{N, \phi}(t)\right) \\ = & \left\{\left(\frac{\left(\lambda_{1, \phi}(t)+\lambda_{N, \phi}(t)+360^{\circ}\right) \bmod 360^{\circ}}{2}\right)\right. \\ & \left.+360^{\circ}\right\} \bmod 360^{\circ}-180^{\circ} \\ = & \lambda_{\text {cross }, \phi}(t), \end{aligned}$$게산된 [TeX:] $$\lambda_{\text {cross }, \phi}(t)$$와 λ를 비교하여 첫 번째 궤도와 마지막 궤도 중 더 가까운 궤도의 위성과 연결된다. [TeX:] $$\lambda_{\text {cross }, \phi}(t)$$와 λ를 비교를 통해 위성을 선택하는 수식은 다음과 같다.
(5)
[TeX:] $$\begin{aligned} g\left(\lambda, \lambda_{\text {cross }, \phi}(t)\right)= & \left(\lambda-\lambda_{\text {cross }, \phi}(t)\right. \\ & \left.+360^{\circ}\right) \bmod 360^{\circ}, \end{aligned}$$
(6)
[TeX:] $$S_{\text {target }}(t)=\left\{\begin{array}{lc} S_1^*(t), & \text { if } g\left(\lambda, \lambda_{\text {cross }, \phi}(t)\right) \lt 180^{\circ}, \\ S_N^*(t), & { otherwise, } \end{array}\right.$$[TeX:] $$S_{\text {target }}(t)$$은 연결되는 위성을 의미하며, [TeX:] $$S_n^*(t)$$는 n번째 궤도에 있는 위성 중 제일 가까운 위성을 의미한다.
제안하는 cross-seam 핸드오버 기법은 위성의 위치 정보와 단절 구간의 경계 조건을 바탕으로 동작한다. 위성 및 궤도의 위도, 경도 정보와 지상국의 위치 정보만으로 핸드오버를 수행하며, TLE(Two-Line Element) 기반 궤도 정보와 ISL 연결 규칙을 통해 유효한 링크 상태 정보를 계산한다[14]. 또한, 제안하는 알고리즘은 지구 자전 동안 cross-seam 핸드오버 횟수를 최대 2회로 제한함으로써 라우팅 테이블 관리의 복잡도를 줄이고, 시스템의 전반적인 제어 복잡도도 감소시킨다. 따라서, 제안하는 기법은 복잡한 연산 없이도 궤도 및 링크 정보를 기반으로 단순한 조건 비교 및 테이블 갱신만으로 가능하며, 실제 저궤도위성 네트워크 운용시스템에 효과적으로 적용될 수 있다.
Ⅴ. 성능 분석가
5.1 시뮬레이션 환경
본 논문에서는 MATLAB Satellite Communications Toolbox를 활용하여 OneWeb의 위성 배치를 기반으로 시뮬레이션을 수행하였으며, cross-seam 구간에서의 공전 주기를 고려하여 24시간 동안 발생하는 핸드오버를 분석한다. 위성 네트워크의 세부 파라미터는 표 1과 같으며, 인접 궤도에 있는 위성 간 위상 차이는 동일 궤도 내 인접 위성 간 위상 차이의 절반이 되도록 인접 궤도 위성 간 위상 상수(phasing factor)를 6으로 가정한다[4]. 또한, 극지역 통신 제한 구간은 [TeX:] $$70^{\circ}$$ 이상의 영역으로 정의하며, 지상국 및 사용자가 위성과 연결할 수 있는 최소 고도각은 [TeX:] $$25^{\circ}$$로 설정한다. 핸드오버 기법에 따른 지구의 자전 주기 동안 위성 네트워크 변화를 분석한다.
표(Table) 1.
| Parameters | Value |
|---|---|
| Altitude | 1,200 km |
| Number of total satellites | 588 |
| Number of orbits (N) | 12 |
| Number of satellites in each orbit (M) | 49 |
| Inclination (α) | [TeX:] $$87.9^{\circ}$$ |
| Phasing factor | 6 |
| Polar region | [TeX:] $$70^{\circ}$$ |
핸드오버 기법 따른 성능을 분석하기 위해, 지상국의 위치를 적도에서 극지역 통신 제한 구간까지 [TeX:] $$10^{\circ}$$ 간격으로 배치하여 cross-seam 핸드오버 발생 횟수, cross-seam 핸드오버 통신 중단시간 등을 분석한다. 또한, OneWeb의 위성 배치에서 궤도 경사각을 [TeX:] $$95^{\circ}, 90^{\circ}, 85^{\circ} $$로 변경하여 시나리오를 구성한다. 이를 바탕으로, 위성의 궤도 경사각에 따른 중위도(위도 [TeX:] $$45^{\circ}$$)에서 cross-seam 핸드오버 중단 지연 시간을 분석하고, 제안하는 핸드오버 알고리즘이 다양한 궤도 경사각 조건에도 적용 가능한지 검증한다.
5.2 시뮬레이션 결과 및 분석
제안한 cross-seam 핸드오버 기법의 성능을 검증하기 위해, 제안하는 cross-seam 핸드오버 기법과 지상국과 가까운 위성으로 핸드오버를 수행하는 거리 기반 기법을 비교한다. 두 기법에 대해 위도에 따른 cross-seam 핸드오버 발생 횟수 및 통신 중단시간 등을 분석하여 성능 차이를 확인한다.
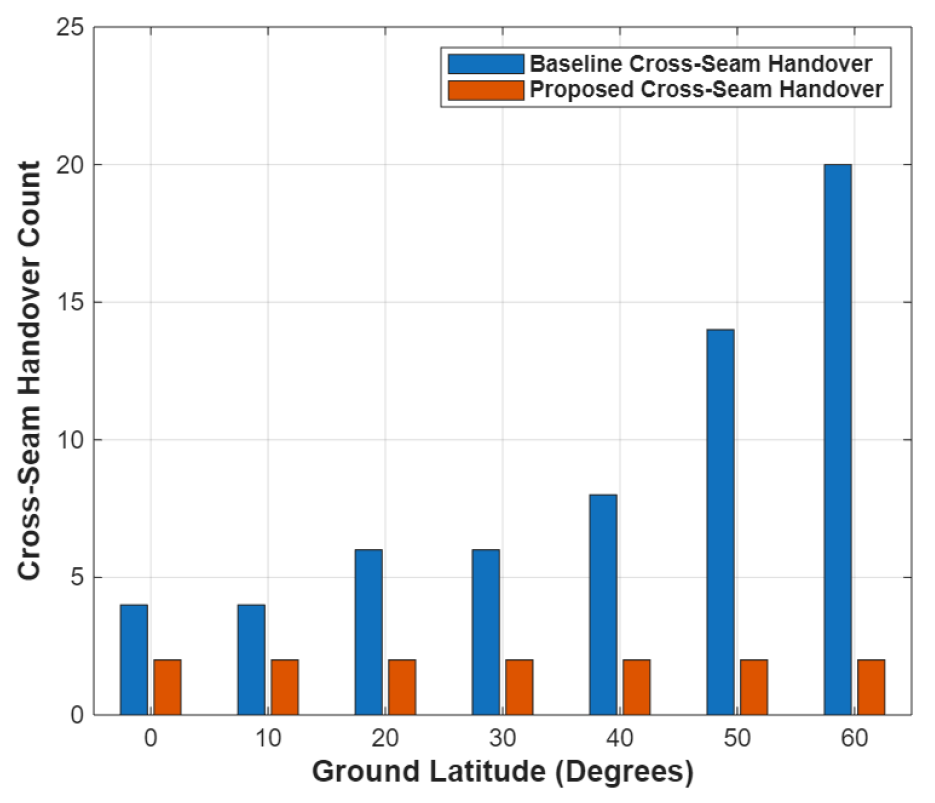
그림 4는 핸드오버 방식에 따른 위도별 cross-seam 핸드오버 발생 횟수를 나타낸다. 기존 핸드오버 방식은 cross-seam 핸드오버 횟수가 최대 20회까지 증가하며, 평균 8.9회 cross-seam 핸드오버가 발생한다. 반면, 제안하는 핸드오버 방식은 cross-seam 핸드오버 횟수를 2회로 제한함으로써, 기존 핸드오버 방식 대비 평균 77%, 최대 90%까지 cross-seam 핸드오버가 감소하는 것으로 나타난다. 이는 위도가증가할수록 궤도 간거리가 감소하여 기존 핸드오버 방식에서는 빈번한 cross-seam 핸드오버가 발생하기 때문이다.
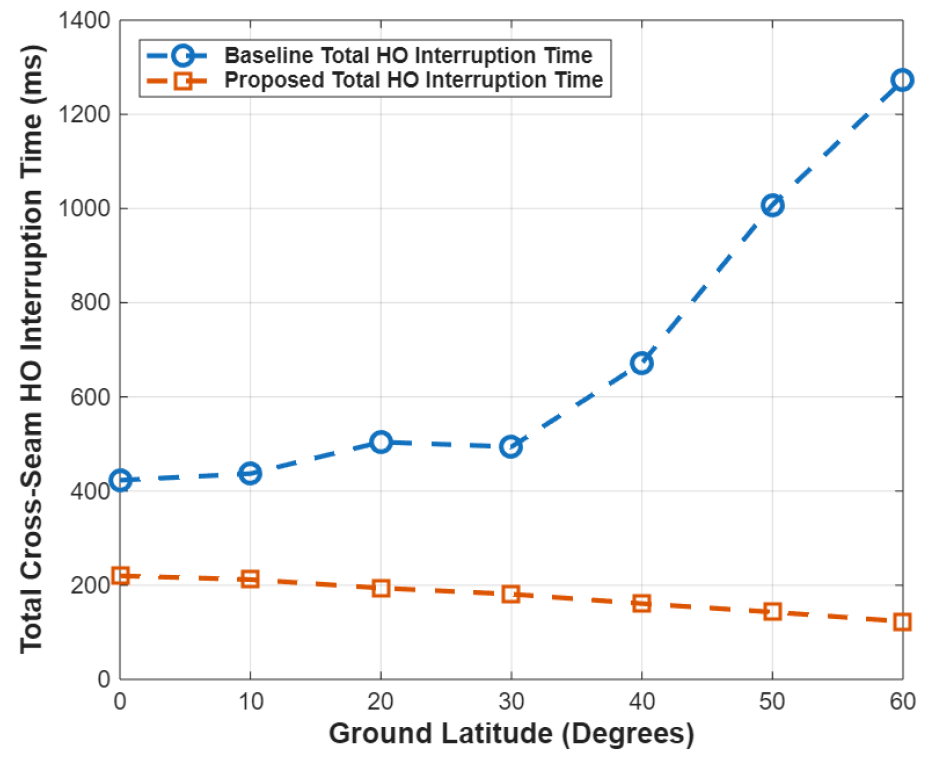
그림 5는 핸드오버 방식에 따른 위도별 cross-seam 핸드오버 통신 중단시간을 나타낸다. 기존 핸드오버 방식에서는 위도가 증가할수록 cross-seam 핸드오버 통신 중단시간이 423 ms에서 최대 1,268 ms까지 증가한다. 이는 위도가 높아질수록 cross-seam 핸드오버 발생 횟수가 증가하여 전체 통신 중단시간이 증가하기 때문이다. 제안한 핸드오버 기법은 cross-seam 핸드오버 횟수를 감소시켜, 통신 중단시간을 220 ms 이하로 유지한다. 제안한 핸드오버 기법은 위도가 증가할수록 cross-seam 핸드오버에 필요한 ISL 수가 감소함에 따라, 핸드오버 통신 중단시간이 123 ms까지 감소한다. 높은 위도일수록 제안한 핸드오버 기법이 cross-seam 핸드오버 통신 중단시간을 크게 줄이며, 최대 90%까지 통신 중단시간이 감소한다.
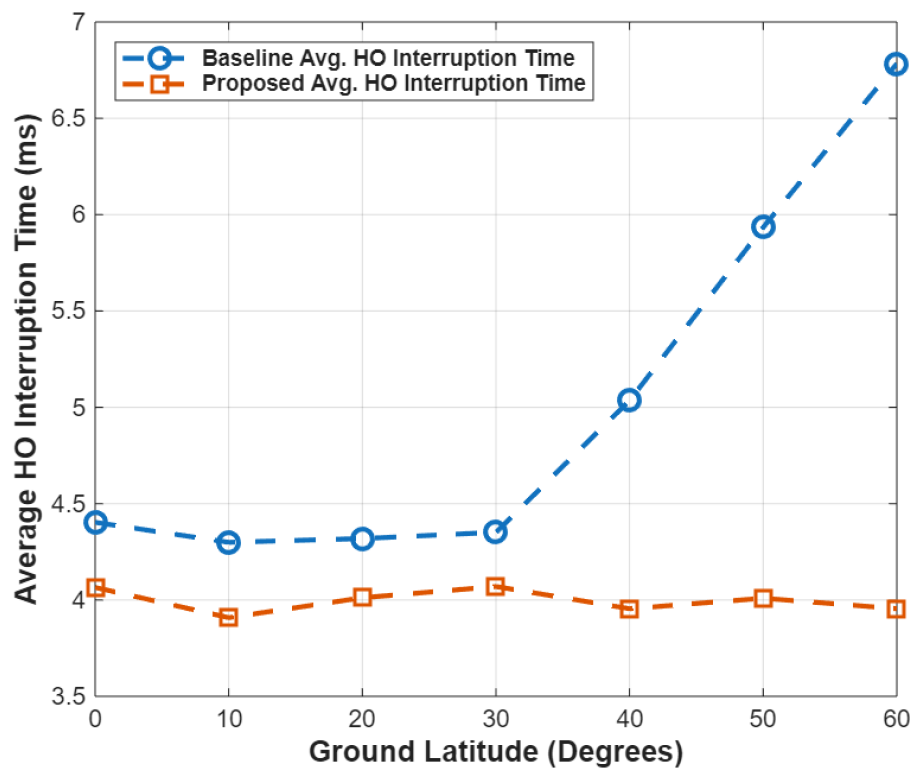
그림 6은 기존 핸드오버 방식과 제안한 핸드오버 방식에 따른 위도별 평균 핸드오버 통신 중단시간 변화를 나타낸다. 기존 핸드오버 방식은 위도 [TeX:] $$40^{\circ}$$ 이하에서는 평균 통신 중단시간이 약 4.4 ms로 일정하게 유지되고, 위도 [TeX:] $$40^{\circ}$$ 이상부터는 점진적으로 증가하여 최대 6.8 ms까지 증가한다. 반면, 제안하는 핸드오버 기법은 핸드오버 평균 통신 중단시간이 약 4 ms로 유지된다. 이는 제안하는 핸드오버 기법이 평균 핸드오버 통신 중단시간을 최소 9% 이상 감소시키며, 최대 41%까지 감소시킨다.
그림 7은 핸드오버 방식에 따른 위도 별 핸드오버 과정에서 필요한중계 위성 수를나타낸다. 기존핸드오버 방식은 [TeX:] $$30^{\circ}$$를 제외하고 위도가 증가할수록 필요한 중계 위성의 수 역시 증가한다. 이는 중계 위성이 필요한 상황이 cross-seam 핸드오버에서 발생하며, 위도가 증가할수록 해당 구간에서의 핸드오버 횟수가 증가함에 따라 중계 위성의 요구 수가 늘어나기 때문이다. 그러나 위도 [TeX:] $$30^{\circ}$$에서는 위도 [TeX:] $$20^{\circ}$$에서와 같은 수의 cross-seam 핸드오버가 발생하고, 필요한 ISL 수는 감소한다. 제안하는 핸드오버 기법은 위도에 상관없이 cross-seam 핸드오버가 2번만 발생하며, 위도가 증가할수록 ISL 수가 64에서 36까지 필요한 중계 위성 수가 감소한다. 따라서 제안하는 핸드오버 기법을 사용하는 경우 중계 위성을 최대 339개를 감소시키며, 평균 210.9개에서 51.7개로 감소시킨다.
그림(Fig.) 7.
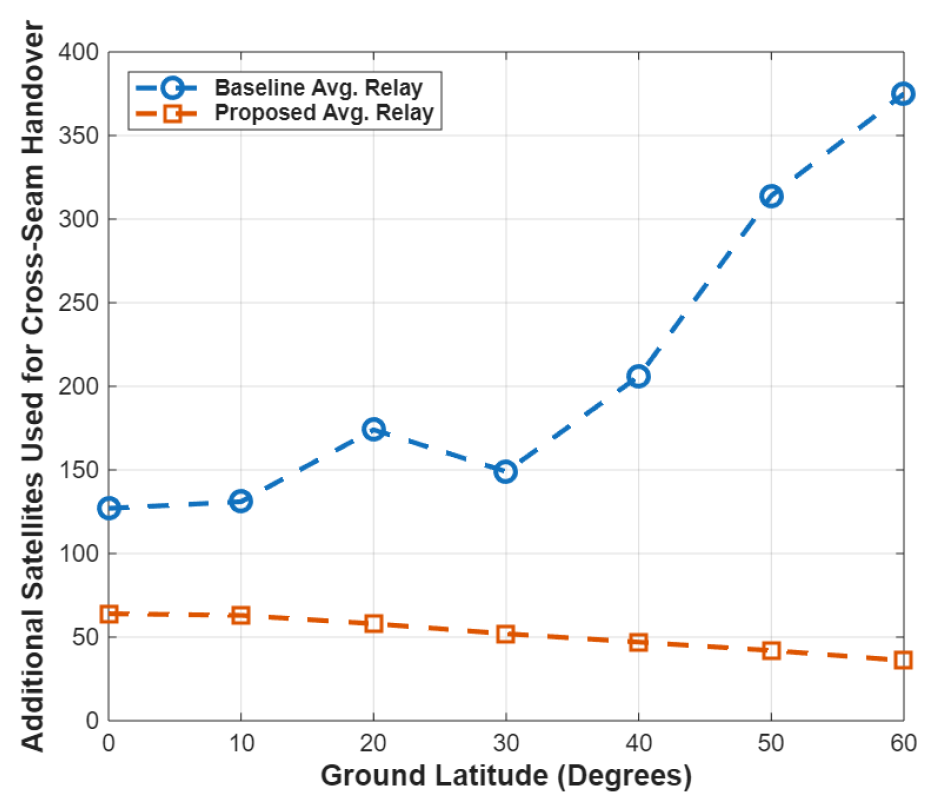
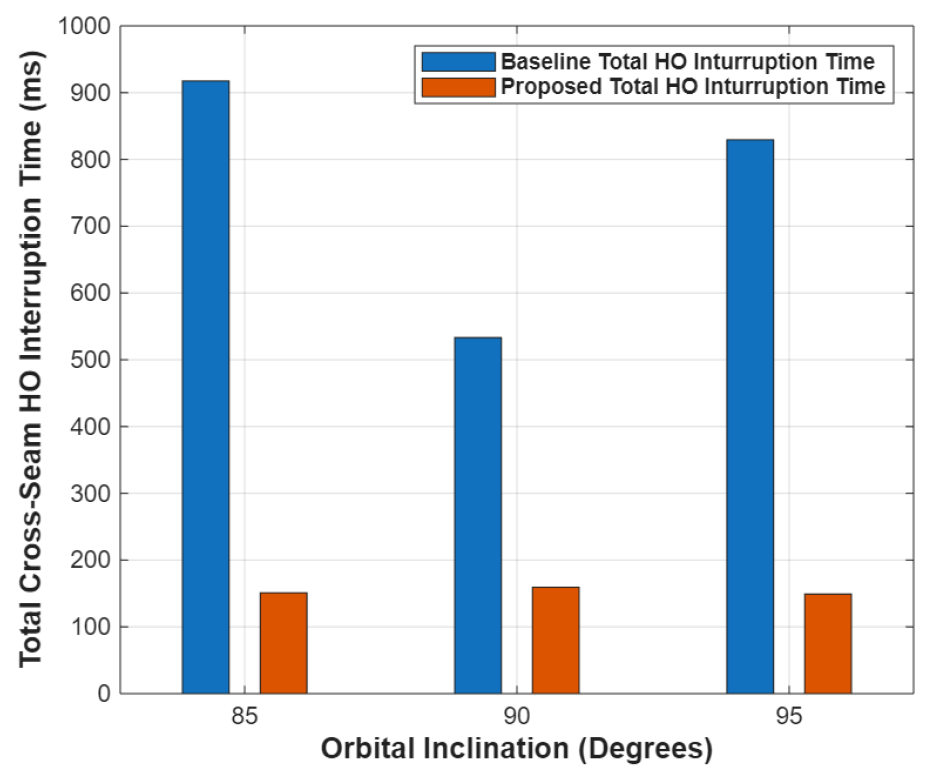
그림 8은 중위도 지역에서 궤도 경사각에 따른 cross-seam 핸드오버 통신 중단시간을 나타낸다. 분석 결과 [TeX:] $$95^{\circ}, 90^{\circ}, 85^{\circ} $$의 궤도 경사각에서 각각 680 ms, 374 ms, 767 ms가 감소한다. 따라서, 제안한 핸드오버 기법은 다양한 궤도 경사각 조건에서도 일관된 성능을 유지하며, 핸드오버 통신 중단시간을 효과적으로 감소시킨다.
그림(Fig.) 8.
기존 핸드오버 방식은 cross-seam 핸드오버 발생 횟수가 많고, 통신 중단시간이 긴 문제점이 발생한다. 이러한 통신 중단은 실시간 서비스 제공을 위한 연속적인 데이터 전송을 불가능하게 하며, 패킷 손실률 증가, 지연 시간의 불안정성 등의 문제를 발생시킨다. 따라서, 제안한 핸드오버 기법을 통해 핸드오버 통신 중단시간을 줄이는 것은 사용자의 안정적인 연결이 필요한 서비스나 실시간 응용 서비스 제공이 가능하다.
Ⅵ. 결 론
본 논문에서는 궤도와 위성의 위도 및 경도 정보를 활용하여 cross-seam 핸드오버를 수행하는 방법을 제안하였다. 성능 분석 결과, 제안한 방법이 기존 방식보다 모든 위도에서 평균 핸드오버 통신 중단시간을 감소시키는 결과를 확인할 수 있었다. 기존 방식은 위도가 증가함에 따라 평균 핸드오버 통신 중단시간이 증가하지만, 제안하는 방법은 거의 일정하게 유지되는 것을 확인하였다. 이는 위성의 이동에 따른 핸드오버 과정에서 라우팅 경로 변화가 적게 발생함을 시사한다. 또한, 궤도 경사각에 따른 핸드오버 통신 중단시간을 비교하여 다양한 궤도 경사각 조건에서 통신 성능 개선을 확인하였다.
본 연구는 시뮬레이션 기반으로 수행되었으며, 실제 위성에서의 신호 세기, 채널 품질 변동, 궤도 오차 등은 고려되지 않았다. 향후 연구에서는 이러한 변수들을 반영한 핸드오버 전략의 고도화 및 on-board 시스템에서의 구현 가능성에 대한 검토가 필요할 것이다.
Biography
Biography
Biography
Biography
Biography
References
- 1 G. Choi and Y. Song, "Low earth orbit satellite communications, applications and major operators’ service deployments," Electr. and Telecommun. Trends, vol. 39, no. 3, pp. 36-47, Jun. 2024. (https://doi.org/10.22648/ETRI.2024.J.390304)doi:[[[10.22648/ETRI.2024.J.390304]]]
- 2 H. Cha, J. Kim, N. Lim, J. Lee, and Y. Ko, "A survey on inter-satellite links for low-earth orbit satellite," J. KICS, vol. 47, no. 10, pp. 1508-1518, Oct. 2022. (https://doi.org/10.7840/kics.2022.47.10.1508)doi:[[[10.7840/kics.2022.47.10.1508]]]
- 3 H. Kokkoniemi-Tarkkanen, et al., "Missioncritical connectivity over LEO satellites: Performance measurements using OneWeb system," IEEE Aerospace and Electr. Syst. Mag., vol. 40, no. 2, pp. 18-30, Feb. 2025. (https://doi.org/10.1109/MAES.2024.3490538)doi:[[[10.1109/MAES.2024.3490538]]]
- 4 H. Song, J. Lee, and Y. Yi, "Feasibility study of communication access via Iridium constellation for small-scale magnetospheric ionospheric plasma experiment mission," J. Astronomy and Space Sci., vol. 39, no. 3, pp. 109-116, Sep. 2022. (https://doi.org/10.5140/JASS.2022.39.3.109)doi:[[[10.5140/JASS.2022.39.3.109]]]
- 5 Q. Chen, J. Guo, L. Yang, X. Liu, and X. Chen, "Topology virtualization and dynamics shielding method for LEO satellite networks," IEEE Commun. Lett., vol. 24, no. 2, pp. 433437, Feb. 2020. (https://doi.org/10.1109/LCOMM.2019.2958132)doi:[[[10.1109/LCOMM.2019.2958132]]]
- 6 L. Zhang, et al., "A routing algorithm based on link state information for LEO satellite networks," in Proc. 2020 IEEE Globecom Wkshps., pp. 1-6, Dec. 2020. (https://doi.org/10.1109/GCWkshps50303.2020. 9367496)doi:[[[10.1109/GCWkshps50303.2020.9367496]]]
- 7 O. Markovitz and M. Segal, "Seam-aware location-based random walk routing algorithms for low orbit satellite constellations," in Proc. 2021 17th Int. Conf. Wireless and Mobile Computing, Netw. and Commun., pp. 351-356, Bologna, Italy, Oct. 2021. (https://doi.org/10.1109/WiMob52687.2021.960 6291)doi:[[[10.1109/WiMob52687.2021.9606291]]]
- 8 A. Al-Hourani, "Session duration between handovers in dense LEO satellite networks," IEEE Wireless Commun. Lett., vol. 10, no. 12, pp. 2810-2814, Dec. 2021. (https://doi.org/10.1109/LWC.2021.3118214)doi:[[[10.1109/LWC.2021.3118214]]]
- 9 E. A. Elbehiry, A. Fares, B. M. Elhalawany, and H. A. TagEldein, "Inter-mesh routing algorithm in LEO satellite constellations networks," Computing, Jan. 2025. (https://doi.org/10.1007/s00607-024-01409-4)doi:[[[10.1007/s00607-024-01409-4]]]
- 10 T. S. Abdu, et al., "Demand-aware flexible handover strategy for LEO constellation," in Proc. 2023 IEEE Int. Conf. Commun. Wkshps., pp. 978-983, Oct. 2023. (https://doi.org/10.1109/ICCWorkshops57953.2 023.10283793)doi:[[[10.1109/ICCWorkshops57953.2023.10283793]]]
- 11 T. Lan, D. Zhou, M. Sheng, and J. Li, "Inter-satellite link planning for high capacity in LEO mega-constellations," in Proc. IEEE Int. Conf. Commun., pp. 4451-4456, Aug. 2024. (https://doi.org/10.1109/ICC51166.2024.106223 03)doi:[[[10.1109/ICC51166.2024.10622303]]]
- 12 Z. Yi, L. Jun, S. Qian, J. Yong, and H. Yanlang, "Topology control strategy of LEO satellite constellation based on optimal polar boundary," in Proc. Int. Conf. Electr., Commun. and Control, pp. 4605-4608, Sep. 2011. (https://doi.org/10.1109/ICECC.2011.6066405)doi:[[[10.1109/ICECC.2011.6066405]]]
- 13 X. Liu, X. Yan, Z. Jiang, C. Li, and Y. Yang, "A low-complexity routing algorithm based on load balancing for LEO satellite networks," in Proc. 2015 IEEE 82nd Veh. Technol. Conf., Sep. 2015. (https://doi.org/10.1109/VTCFall.2015.7390795)doi:[[[10.1109/VTCFall.2015.7390795]]]
- 14 X. Gong, et al., "Precise onboard real-time orbit determination with a low-cost singlefrequency GPS/BDS receiver," Remote Sensing, Jun. 2019. (https://doi.org/10.3390/rs11111391)doi:[[[10.3390/rs11111391]]]