Semyoung Oh and Seongbin An
Vehicle Platooning Communication Using Auxiliary Beam-Assisted Tracking Scheme
Abstract: This paper applies an auxiliary beam-assisted beam tracking method to achieve stable beam align- ment and effective beamforming for high-speed com- munication between vehicles in a platooning scenario. To evaluate the effectiveness of the applied method, a vehicle dynamics and wireless communication envi- ronment were modeled. Furthermore, its data trans- mission performance was also compared with that of a location-based method through random simulations.
Keywords: Vehicle platooning , beamforming , auxiliary beam , beam tracking
Ⅰ. 서 론
최근 유․무인 및 자율주행 기술의 발전과 함께 종속 주행 또한 주목받고 있다[1]. 종속주행은 복수의 차량이 동일 경로를 따라 주행하는 방식으로 추종 차량은 선행 차량에서 관측 및제공된 정보를 활용, 주행환경에 대한 예측으로 더욱 안전하고 효율적인 주행이 가능하다. 이러한 정보는 보행자 등의 주변 환경을 포함한 고해상도 이미지이나 영상일 수 있으며, 이를 원활하게 전달하기 위해서는 고속 데이터 통신이 필요하다. 빔포밍(Beamforming)은 안테나 배열을 통해 특정 방향으로 에너지를 집중시키는 기술로 차량간 (Vehicle-to-Vehicle, V2V) 통신에서 전송 속도 개선 목적으로 활발히 연구되고 있다[2]. 하지만, 곡선 도로 주행 시 차량간 상대위치 변화로 원활한 빔포밍 통신을 위해서는 지속적인 빔 정렬이 필요하며, 이를 위해 빔 훈련(Beam training)이 활용될 수 있다[3]. 해당 기법은 채널의 이득과 도래각(Angle of Arrival, AoA) 추정을 매 전송 블록마다 실시하여, 높은 정확도의 빔 정렬을 이룰 수 있으나 과도한 오버헤드(overhead)로 통신 지연 또한 발생시킬 수 있다. 이러한 빔 훈련 기법의 대안으로 상대적으로 낮은 오버헤드를 요하는 위치정보 기반 빔 추적(Beam tracking) 방식 또한 고려될 수 있으나 위치정보 오차 및 낮은 갱신속도 등으로 인한 빔 정렬 정확도 저하가 발생할 수 있다[4].
본 논문은 곡선 도로 종속주행간 V2V 빔포밍 통신에 보조 빔(Auxiliary beam) 기반 빔 추적 기법 적용을 제안한다[5]. 해당 기법은 추적 주기내 차량간 벡터각 변화는 미미하다는 가정하에 이전 빔 지향각 주변으로 보조 빔을 조사하고 분석하여 현재 지향각을 추정한다.
이어지는 장에서는 두 대의 차량으로 구성된 종속 주행 시나리오를 기반으로 차량 주행과 무선채널 모델을 제시하고, 이를 바탕으로 시뮬레이션을 수행하여 위치 정보 기반 대비 보조 빔 추적 기법의 우수성을 확인하였다.
Ⅱ. 종속주행 모델
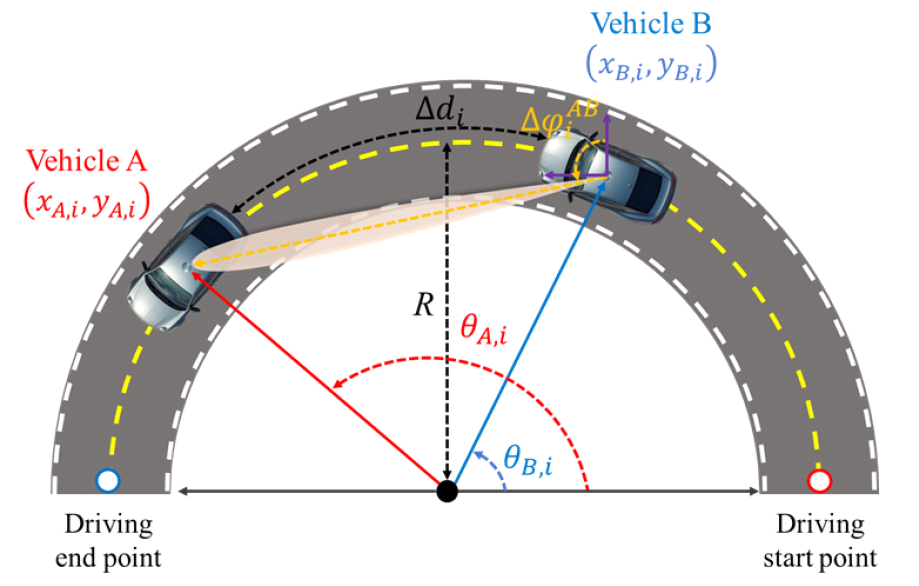
본 논문에서 차량 A (선행) 및 차량 B (추종)는 그림 1과 같이 x - y 평면상 반지름이 R인 반원 궤적을 반시계 방향 및 속도 v로 시간 [TeX:] $$T=(\pi R-D) / v$$ 동안 주행하며 차량 A가 종료지점에 도달 시 두 차량 모두 주행을 중지한다. 주행상태는 [TeX:] $$\Delta t$$ 간격으로 갱신되며, 등속도 주행 시 각 차량의 방위각은 [TeX:] $$\theta_{A, i}=\omega i \Delta t-\pi / 2+D / R$$ 및 [TeX:] $$\theta_{B, i}=\omega i \Delta t-\pi / 2$$, 위치는 다음과 같이 정의된다.
(1)
[TeX:] $$\begin{array}{r} x_{A, i}=R \cos \left(\theta_{A, i}\right), y_{A, i}=R \sin \left(\theta_{A, i}\right) \\ x_{B, i}=R \cos \left(\theta_{B, i}\right), y_{B, i}=R \sin \left(\theta_{B, i}\right) \end{array}$$(1)에서 [TeX:] $$i=0,1, \cdots, T / \Delta t, \omega=v / R \text { 및 } D=\delta_D \pi R$$는 각각 시간지표, 각속도 및 차간거리이다.
실제 주행환경에서는 다양한 외적 요소에 의해 차간 거리를 지속적으로 동일하게 유지하는 것이 제한된다. 따라서, 이러한 점을 반영함과 동시에 차량 주행 모델을 단순화하기 위해 차량 B의 속도만 [TeX:] $$P_v$$의 확률로 [TeX:] $$v_{B, i}=v_{B, i-1}+\Delta v$$와 같이 갱신되며, [TeX:] $$\Delta v \text { 는 } \delta_v U[0,1]$$의 균일분포를 따른다고 가정하였다. 또한 이러한 속도 변화로 인해 발생할 수 있는 차량 A와의 충돌을 방지하기 위해, 차간거리인 [TeX:] $$\Delta d_i=R\left|\theta_{A, i}-\theta_{B, i}\right| \text { 가 } \Delta d_{\min }=\delta_m D$$ 이하로 감소 시 차량 B의 속도를 [TeX:] $$\Delta v=\left(\Delta d_{\min }-\Delta d_i\right)/ \Delta t \text { 및 } v_{B, i}=\max \left(v_{B, i-1}-\Delta v, 0\right)$$와 같이 감속한다. 결과적으로 차량 B의 위치 방위각은 [TeX:] $$\omega_{B, i}=v_{B, i} / R$$와 함께 [TeX:] $$\theta_{B, i}=\theta_{B, i-1}+i \Delta t \omega_{B, i-1}$$와 같이 재정의 된다.
Ⅲ. 빔 추적 기법
본 장에서는 종속주행시 차량간 데이터 전송에 활용할 수 있는 빔 추적 기법에 대해 논하고자 한다. 우선, 차량 A는 전방향성(Omni-directional) 안테나를 통해 주행간 획득한 정보를 송신하고 차량 B는 [TeX:] $$N_A$$개의 안테나로 이루어진 균일선형배열(Uniform Linear Array, ULA)를 통해 수신 받는 경우를 고려한다. 여기서, 안테나간 간격은 반파장이며 가시선(Line of Sight, LOS)이 유지된다고 가정한다. ULA의 조향벡터(steering vector)는 [TeX:] $$\widetilde{\varphi}=-\pi \cos (\varphi) \text { 및 } \varphi \in[-\pi, \pi)$$와 함께 수식 (2)와 같이 정의되며,
(2)
[TeX:] $$\boldsymbol{a}(\tilde{\varphi})=\frac{1}{\sqrt{N_A}}\left[1, e^{j \widetilde{\varphi}}, \cdots e^{j\left(N_A-1\right) \widetilde{\varphi}}\right]^T \in \mathbb{C}^{N_A \times 1},$$i번째 전송 블록에서 수식 (3)의 무선채널을 통해 시험 신호를 전송할 경우 차량 B에서의 수신 신호는 수식 (4)와 같이 정의된다.
(3)
[TeX:] $$\boldsymbol{H}_i=\sum_{l=0}^L\left|\alpha_l\right| e^{-j \Delta d_i^e} \boldsymbol{a}\left(\tilde{\varphi}_l\right)^H$$
위의 식에서 L은 신호 경로의 개수, [TeX:] $$\alpha_l \text { 및 } \tilde{\varphi}_l=-\pi \cos \left(\varphi_l\right)$$은 각각 I번째 신호의 채널 이득 및 AoA, [TeX:] $$\Delta d_i^e=\left\|\boldsymbol{X}_{A B, i}\right\|$$은 차량 A와 B간 거리이다. 참고로, [TeX:] $$\boldsymbol{X}_{A B, i}=\left(x_{A B, i}, y_{A B, i}\right)$$는 [TeX:] $$x_{A B, i}=x_{A, i}-x_{B, i} \text { 및 } y_{A B, i}=y_{A, i}-y_{B, i} .$$로 정의되는 상대위치 벡터이다. 그리고 l > 0인 경우, [TeX:] $$\alpha_l \text { 와 } \varphi_l$$은 각각 정규분포 [TeX:] $$N\left(0, \sigma_l\right)$$ 및 균일분포 [TeX:] $$U[0, \pi]$$를 따르며, l=0인 경우 LOS 신호임으로 [TeX:] $$\alpha_0=1 \text { 및 } \tilde{\varphi}_0=-\pi \cos \left(\Delta \varphi_i^{A B}\right)$$이다. 이때, [TeX:] $$\Delta \varphi_i^{A B}=\tan ^{-1}\left(x_{A B, i} / y_{A B, i}\right)$$은 차량간 벡터각이며, 채널 이득은 [TeX:] $$\sum_{l=0}^L\left|\alpha_l\right|^2=1$$와 같이 정규화된다. 추가적으로, [TeX:] $$P_t$$는 송신전력 [TeX:] $$\boldsymbol{W}_i=\boldsymbol{a}\left(\tilde{\varphi}_i\right) \in \mathbb{C}^{N_A \times 1}$$는 빔포임 벡터, s는 단위전력을 가지는 시험 신호 그리고 [TeX:] $$n_i \text { 은 } N_0$$의 전력을 가지는 가우시안 잡음이다.
곡선 구간 주행간 주기적인 빔 정렬이 이루어지지 않을 경우 통신 품질 저하 나아가 두절 상태에 이를 수 있다. 이는 차량 B에서 생성된 빔이 차량 A를 적절히 조사하지 않아 수신 신호의 SNR (Signal-to-Noise Ratio)이 대폭 감소할 수 있기 때문이다. 이러한 문제를 해결하기 위해 본 논문에서는 보조 빔을 활용하는 빔 추적 기법을 적용[5], [TeX:] $$\Delta \varphi_i^{A B}$$를 추정하는 것을 제안한다. 구체적으로 차량 B는 [TeX:] $$\tilde{\varphi}_{i-1}-\Delta \varphi \text { 및 } \tilde{\varphi}_{i-1}+\Delta \varphi$$ 방향으로 보조 빔 [TeX:] $$\left(\Delta \varphi=\delta_w \pi / N_a\right)$$을 생성하여 시험 신호를 전송하고 차량 A는 수식 (5)의 SNR을 측정하여 차량 B에서 회신하며, 차량 B는 해당 정보를 활용하여 수식 (6)과 같이 [TeX:] $$\tilde{\varphi}_i$$를 갱신하다. 참고로, [TeX:] $$\tilde{\varphi}_i$$는 i에서 추정된 차량 A와 B간 벡터각이다.
(5)
[TeX:] $$\gamma_i^L=P_t N_A\left|\boldsymbol{H}_i \boldsymbol{W}_i^L\right|^2 / N_0, \quad \gamma_i^R=P_t N_A\left|\boldsymbol{H}_i \boldsymbol{W}_i^R\right|^2 / N_0$$
(6)
[TeX:] $$\tilde{\varphi}_i=\tilde{\varphi}_{i-1}-\sin ^{-1}\left(\frac{\varepsilon_i \sin (\Delta \widetilde{\varphi})-\varepsilon_i \sqrt{1-\varepsilon_i^2} \sin (\Delta \widetilde{\varphi}) \cos (\Delta \widetilde{\varphi})}{\sin ^2(\Delta \widetilde{\varphi})+\varepsilon_i^2 \cos ^2(\Delta \widetilde{\varphi})}\right)$$여기서, [TeX:] $$\boldsymbol{W}_i^L=\boldsymbol{a}\left(\varphi_{t, i}+\widetilde{\varphi}_{i-1}-\Delta \varphi\right)$$ 및 [TeX:] $$\boldsymbol{a}\left(\varphi_{t, i}+\widetilde{\varphi}_{i-1}+\Delta \varphi\right)$$는 보조 빔의 빔포밍 벡터이며, [TeX:] $$\varepsilon_i \text {는 }\left(\gamma_i^L-\gamma_i^R\right) /\left(\gamma_i^L+\gamma_i^R\right), \varphi_{t, i}$$는 ULA의 기울기 각으로 정의된다. 또한, 수식 (6)은 i - 1및 전송 블록간 차량의 위치와 채널은 불변이며, i = 0에서의 두 차량의 위치는 정확히 알고 있다는 가정하에 유도되었다. 마지막으로 추정된 [TeX:] $$\tilde{\varphi}_i$$와 [TeX:] $$\widetilde{\boldsymbol{W}}_i=\boldsymbol{a}\left(\varphi_{t, i}+\tilde{\varphi}_i\right)$$를 기반으로 메인 빔을 생성하여 데이터를 전송하며, 이때 전송률은 수식 (7)과 같다.
(7)
[TeX:] $$\rho_i\left(\widetilde{\varphi}_i\right)=\log _2\left(1+P_t N_A\left|\boldsymbol{H}_i \widetilde{\boldsymbol{W}}_i\right|^2 / N_0\right)$$표(Table) 1.
| Parameters | R | v | [TeX:] $$\Delta t$$ | [TeX:] $$\delta_D$$ | [TeX:] $$\delta_v$$ | [TeX:] $$\delta_m$$ |
| values | 191 [m] | 14 [m/s] | 0.01 [s] | 0.6 | 1 | 0.4 |
| Parameters | [TeX:] $$p_v$$ | L | [TeX:] $$\sigma_L$$ | [TeX:] $$p_t$$ | [TeX:] $$N_0$$ | [TeX:] $$\delta_w$$ |
| values | 0.2 | 4 | 1 | 10 [w] | 1 [w] | 0.5 |
Ⅳ. 시뮬레이션 결과 및 결론
본 장에서는 제시된 기법의 성능 확인을 위해 몬테카를로 시뮬레이션을 실시하였다. 총 1,000개의 샘플을 생성하였으며 이때 표 1의 값들을 이용하였다. 그림 1의 곡선은 [TeX:] $$\rho_i\left(\tilde{\varphi}_i\right)$$의 샘플 평균값이며 차량간 빔 정렬이 이루어지지 않았을 때와 비교하여 위치정보 대비 보조빔 기반 빔 추적 기법의 개선 정도를 보여준다. 이때, 위치정보는 5m CEP (Circular Error Probability)의 정확도 및 10 Hz의 수신 주기를 가지는 위성항법장치를 통해 제공된 것으로 가정하였다. 좌측 그림에서 확인할 수 있듯이, 보조 빔 기반 추적 기법이 전송률 측면에서 우수한 성능을 보이고 있다. 또한, ULA 안테나 개수가 증가함에 따라 두 기법 간의 성능 차가 더욱 뚜렷해졌으며, [TeX:] $$N_A=128$$의 경우 성능차가 [TeX:] $$N_A=32$$일 때와 비교하여 평균적으로 4.75배 크다. 이는 보조 빔 기법의 빔 추적 우수성으로 인해 차량 A가 빔 중심 각 주변에 위치할 가능성이 더욱 높으며 결과적으로 위치정보 기반 대비 배열 이득(array gain) 증가 효과가 두드러지기 때문이다. 실제로 [TeX:] $$N_A=128$$에서 위치정보 기반의 경우 [TeX:] $$\Delta \varphi_i^{A B} \text { 와 } \tilde{\varphi}_i$$간의 RMSE (Root Mean Square Error)는 1.41인 반면 보조 빔은 0.35이다. 추가적으로 우측 그림은 R에 따른 [TeX:] $$\Delta \varphi_i^{A B} \text { 와 } \tilde{\varphi}_i$$간의 RMSE를 보여주고 있으며, 곡률[TeX:] $$(\approx 1 / R)$$이 증가함에도 불구하고 RMSE 증가 정도가 작은 것을 알 수 있다. 마지막으로, 위의 결과는 주행 방향과 무관하며 이는 보조 빔 기반 추적 기법의 대칭성 때문이다.
본 논문에서는 종속주행 빔포밍 통신에서의 보조 빔 기반 빔 추적 기술의 효용성을 확인하였으나 이상적인 조건만 고려하였다는 점에서 한계가 있다. 따라서, 후속 연구에서는 LOS가 단절되거나 곡률이 일정하지 않은 실제 도로 환경에서 제안된 기법의 효과성을 검증할 예정이다.
References
- 1 M. Kang, H. Choi, H. Hong, S. Jang, K. Park, T. Kwon, H. Yun, Y. Cho, and S. Kwon, "Development of an agricultural robot platform for autonomous driving tasks in weeding operations," J. Korean Soc. Manuf. Process Eng., vol. 23, no. 8, pp. 68-76, Aug. 2024. (https://doi.org/10.14775/ksmpe.2024.23.08.068)doi:[[[10.14775/ksmpe.2024.23.08.068]]]
- 2 C. Mahabal, H. Wang, and H. Fang, "Dual mode localization assisted beamforming for mmWave V2V communication," IEEE Trans. Veh. Technol., vol. 71, no. 9, pp. 9450-9459, Sep. 2022. (https://doi.org/10.1109/TVT.2022.3175165)doi:[[[10.1109/TVT.2022.3175165]]]
- 3 S. H. Lim, S. Kim, B. Shim, and J. W. Choi, "Efficient beam training and sparse channel estimation for millimeter wave communications under mobility," IEEE Trans. Commun., vol. 68, no. 10, pp. 6583-6596, Oct. 2020.custom:[[[-]]]
- 4 S. Ozawa, T. Ikuta, Y. Sasaki, R. Iwaki, J. Nakazato, and M. Tsukada, "Location-aided fast beam tracking algorithm for millimeterwave V2I," IEICE Commun. Express, vol. 13, no. 5, pp. 146-150, May 2024. (https://doi.org/10.23919/comex.2024XBL0001)doi:[[[10.23919/comex.2024XBL0001]]]
- 5 D. Zhu, J. Choi, and R. W. Heath, "Auxiliary beam pair enabled AoD and AoA estimation in closed-loop large-scale millimeter-wave MIMO systems," IEEE Trans. Wireless Commun., vol. 16, no. 7, pp. 4770-4785, May 2017. (https://doi.org/10.1109/TWC.2017.2702617)doi:[[[10.1109/TWC.2017.2702617]]]