IndexFiguresTables |
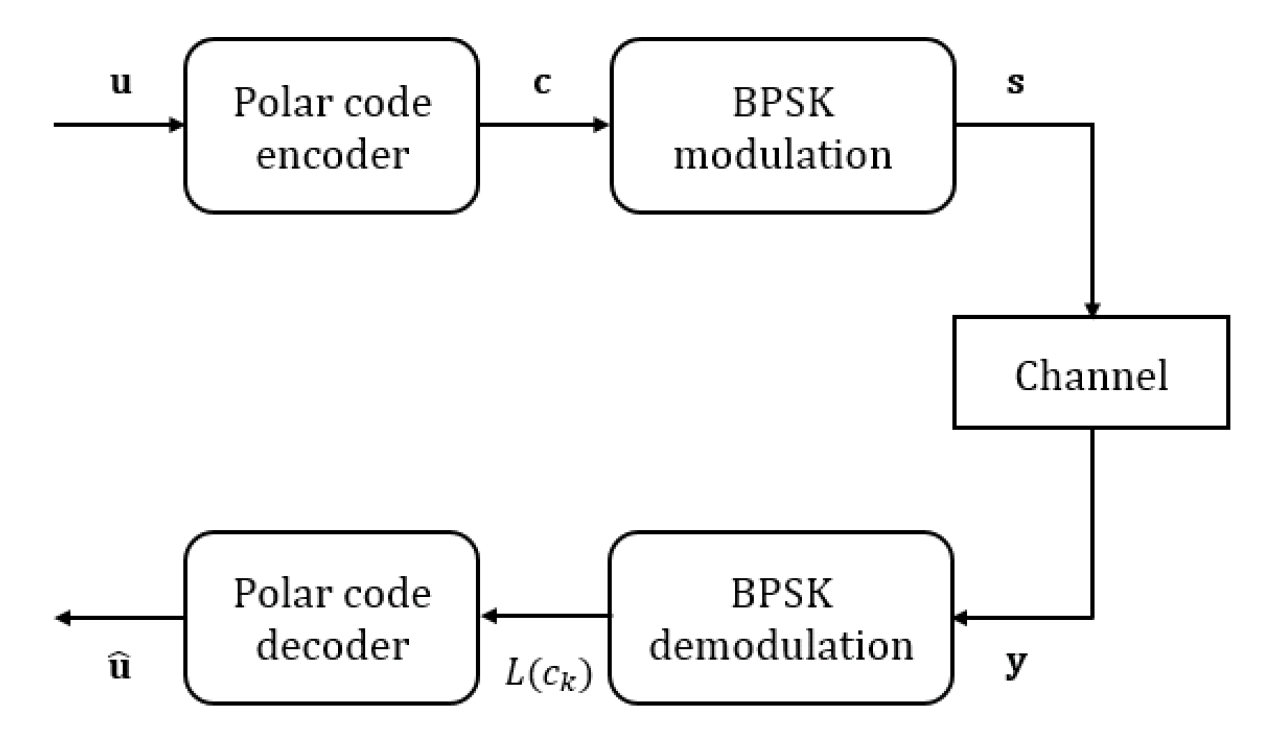
Chungsu Lee♦ , Sungyeol Back* , Chansoo Park* and Wangrok OhºLow Complexity Early Termination Detector for Polar Code Belief Propagation DecodingAbstract: Belief propagation (BP) decoding algorithm was proposed as a low latency decoding algorithm for polar codes. Unfortunately it requires relatively high decoding complexity compared to successive cancellation decoding. To remedy high complexity problem, early termination BP algorithm was proposed which requires additional complexity for stopping criteria test. In this paper, we propose low-complexity early termination detectors based on the characteristics of log-likelihood ratios generated within BP detectors. The proposed detectors offer identical performance with lower complexity compared to conventional detectors. Keywords: Polar code , Early termination belief propagation decoding , Complexity 이충수♦ , 백성열* , 박찬수* , 오왕록º낮은 복잡도의 극 부호 신뢰 전파 복호 조기 종료 판별기요 약: 극 부호 (polar codes) 복호 기법 중 하나로 신뢰 전파 복호 기법 (belief propagation decoding)이 제안되었으 며 연속 제거 복호 기법 (successive cancellation decoding) 대비 지연시간이 짧은 장점이 있으나 계산 복잡도가 높은단점이있다. 이를보완하기위해조기종료신뢰전파복호기법이제안되었으나조기종료여부를판별하 는 데 추가적인 복잡도가 요구된다. 본 논문에서는 극 부호의 신뢰 전파 복호 시 임계 집합 (critical set)의 원소 를 포함하는 하위 극 부호 (sub-polar code)의 복호 과정에서 계산되는 로그 우도 비들의 특징을 활용한 낮은 복 잡도의 조기 종료 판별기들을 제안한다. 제안하는 조기 종료 판별기들은 기존의 조기 종료 판별기들과 동일한 복 호 성능을 제공하며 구현 복잡도를 크게 낮출 수 있다. 키워드: Polar code, Early termination belief propagation decoding, Complexity Ⅰ. 서 론극 부호[1] (polar codes)의 대표적인 복호 기법들로는 연속 제거 (successive-cancellation, SC) 복호 기법[1]과 신뢰 전파 (belief-propagation, BP) 복호 기법[2]을 들 수 있다. BP 복호 기법의 경우 SC 복호 기법대비 복호 지연시간이 짧은 장점이 있으나 미리 설정한 횟수만큼의 반복 복호 수행이 필요하며 이에따라 계산 복잡도가 높은 단점이 있다. 높은 복잡도 문제를 개선하고 복호 지연시간을 더욱 줄이기 위해 특정 조건에서 반복 복호를 종료하는 조기 종료 신뢰 전파 (early termination belief propagation, ET-BP) 복호 기법[3]이 제안되었으며 이를 기반으로 한 다양한 기법들[4,5]이 제안되었다. ET-BP 복호 기법은 신호 대 잡음 비 (signal-to-noise ratio, SNR)가 커질수록 평균 반복 복호 횟수가 줄어들어 평균 계산 복잡도와 지연시간을 크게 줄일 수 있으나 조기 종료 여부를 판별하기 위한 별도의 하드웨어가 필요하며 매 반복 복호마다 해당 하드웨어를 통해 조기 종료 여부를 판별해야 한다. 본 논문에서는 ET-BP 복호 시 극 부호의 임계 집합[6] (critical set)의 원소를 포함한 하위 극 부호 (sub-polar codes)에서 계산되는 로그 우도 비 (log likelihood ratio, LLR)들의 특징을 이용한 낮은 복잡도의 조기 종료 판별기를 제안한다. 제안하는 조기 종료 판별기는 ET-BP 복호기의 성능을 그대로 유지하며 기존에 제안된 조기 종료 판별기보다 낮은 복잡도를 갖는 장점이 있다. 본 논문의 구성은 다음과 같다. 2장에서 극 부호와 극 부호의 BP 복호 기법 및 조기 종료 기준과 조기 종료 판별기의 구조를 설명한다. 3장에서 제안하는 조기 종료 판별기의 구현 방법을 설명하고 4장에서 제안하는 조기 종료 판별기의 성능 및 구현 복잡도를 확인한 후 5장에서 결론을 맺는다. Ⅱ. 시스템 모델본 논문에서 고려하는 시스템 모델은 그림 1과 같다. 극 부호의 메시지 벡터 [TeX:] $$\mathrm{u}=\left[u_0, u_1, \ldots, u_{N-1}\right]$$는 K개의 정보 비트와 (N-K)개의 고정 비트 (frozen bit)로 이루어진다. 극 부호 설계 과정을 통해 생성된 K개의 정보 비트와 (N-K)개의 고정 비트가 각각 매핑될 비트 채널 (bit channel) 인덱스 집합 [TeX:] $$I \text { 및 } I_c$$에 따라 [TeX:] $$\left\{u_k \mid k \in I\right\}$$에는 정보 비트들이 [TeX:] $$\left\{u_k \mid k \in I_c\right\}$$에는 고정비트 '0'이 할당된다. 메시지 벡터 u는 식 (1)을 통해 부호어 (code word) [TeX:] $$\mathrm{c}=\left[c_0, c_1, \ldots, c_{N-1}\right]$$를 생성하며 여기에서 [TeX:] $$\mathrm{G}_N$$은 [TeX:] $$\mathrm{F}=\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right]$$을 [TeX:] $$n=\log _2 N$$차 크로네커 제곱 (Kronecker power) 연산하여 생성된 극 부호 생성행렬(generate matrix)을 나타낸다.
생성된 부호어는 [TeX:] $$s_k=(-1)^{c_k}, k=0,1, \ldots, N-1$$와 같이 BPSK (binary phase shift keying) 변조된 후 양대역 전력 밀도가 [TeX:] $$N_0 / 2$$인 가산성 백색 잡음 채널 (additive white Gaussian noise channel)을 통해 전송되는 것을 가정하였다. 수신 신호는 [TeX:] $$y_k=x_k+n_k, k=0,1, \ldots, N-1$$로 표현할 수 있으며 여기에서 [TeX:] $$n_k$$는 평균이 0, 분산이 [TeX:] $$N_0 / 2$$인 가우시안 랜덤 변수 (Gaussian random variable)이다. 극 부호의 복호는 식 (2)로 계산된 부호 비트별 로그 우도 비 [TeX:] $$L\left(c_k \mid y_k\right)$$를 이용하여 각 복호 기법마다 다양한 방식으로 개의 정보 비트에 대한 로그 우도 비를 계산한 뒤 식 (3)과 같이 [TeX:] $$\hat{u}_k, \quad k \in I$$를 추정한다.
(2)[TeX:] $$L\left(c_k \mid y_k\right)=\ln \frac{P\left(y_k \mid c_k=0\right)}{P\left(y_k \mid c_k=1\right)}$$
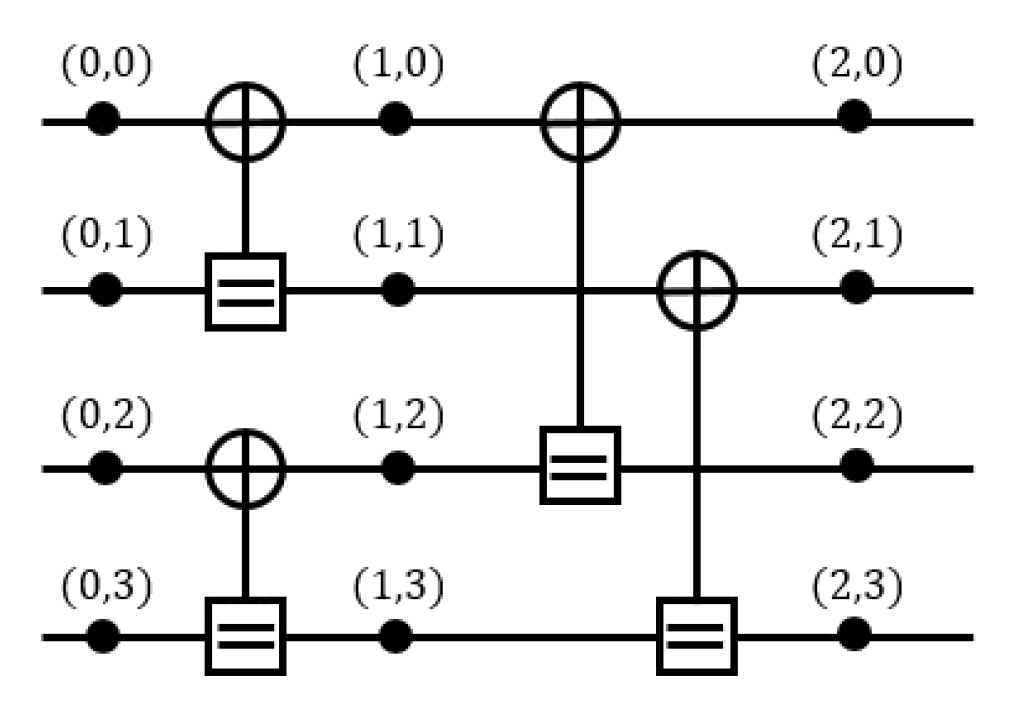
(3)[TeX:] $$L\left(c_k \mid y_k\right)=\ln \frac{P\left(y_k \mid c_k=0\right)}{P\left(y_k \mid c_k=1\right)}$$길이 N=4인 극 부호에 대한 BP 복호기를 팩터 그래프로 도식화하면 그림 2와 같으며 해당 팩터 그래프를 구성하는 단위 팩터 그래프와 복호 과정에서 계산되는 로그 우도 비들을 도식화하면 그림 3과 같다. 그림 2에서 (l,K), [TeX:] $$l=0,1, \ldots, \log _2 N, k=0,1, \ldots, N-1$$은 l번째 단계의 k번째 노드를 나타낸다. BP 복호 기법은 미리 설정된 [TeX:] $$I_m$$ 만큼의 반복 복호를 수행하며 [TeX:] $$t, t=1,2, \ldots, I_m$$번째 반복 복호에서 그림 2의 좌측에서 우측, 우측에서 좌측으로 계산되는 로그 우도 비 [TeX:] $$R_{(l, k)}^t$$와 [TeX:] $$L_{(l, k)}^t$$가 각각 계산된다. 이를 위해 식 (4)와 같은 초기값이 사용되며 매 반복 복호에서는 [TeX:] $$R_{(l, k)}^t$$가 먼저 업데이트된 후 [TeX:] $$L_{(l, k)}^t$$가 업데이트된다.
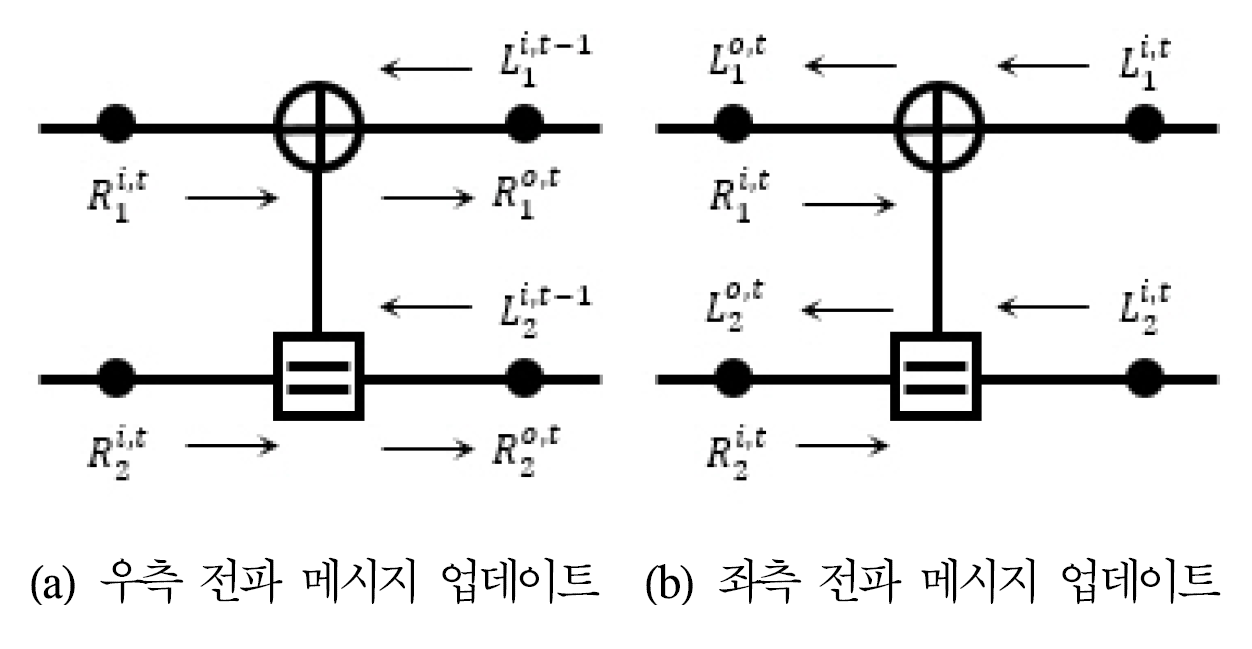
(4)[TeX:] $$\begin{aligned} & L_{(l, k)}^0= \begin{cases}L\left(c_k \mid y_k\right), & l=\log _2 N \\ 0, & \text { otherwise }\end{cases} \\ & R_{(l, k)}^0= \begin{cases}\infty, & l=0, \quad k \in I_c \\ 0, & \text { otherwise }\end{cases} \end{aligned}$$그림 3의 단위 팩터 그래프에서 각 노드의 로그 우도 비들은 식 (5)와 같이 계산되며 이와 동일한 방법으로 그림 2의 (l,k)노드에서의 [TeX:] $$R_{l, k}^t \text { 와 } L_{l, k}^t$$가 계산된다.
(5)[TeX:] $$\begin{aligned} & R_1^{o, t}=f\left(R_1^{i, t}, R_2^{i, t}+L_2^{i, t-1}\right) \\ & R_2^{o, t}=f\left(R_1^{i, t}, L_1^{i, t-1}\right)+R_2^{i, t} \\ & L_1^{o, t}=f\left(L_1^{i, t}, R_2^{i, t}+L_2^{i, t}\right) \\ & L_2^{o, t}=f\left(L_1^{i, t}, R_1^{i, t}\right)+L_2^{i, t} \end{aligned}$$여기에서 [TeX:] $$f(\cdot)$$는 식 (6)과 같이 계산되며 식 (7)과 같은 근사식을 이용하여 로그 우도 비를 계산할 수 있다. 본 논문에서는 식 (7)을 이용하여 로그 우도 비를 계산하는 것을 가정하였다.
(6)[TeX:] $$f\left(L_1, L_2\right)=2 \tanh ^{-1}\left(\tanh \left(L_1 / 2\right) \tanh \left(L_2 / 2\right)\right)$$
(7)[TeX:] $$\approx \operatorname{sign}\left(L_1\right) \operatorname{sign}\left(L_2\right) \times \min \left(\left|L_1\right|,\left|L_2\right|\right)$$모든 반복 복호가 종료된 후에는 식 (8)과 같이 [TeX:] $$u_k$$에 대한 추정값 [TeX:] $$\hat{u}_k$$을 결정한다.
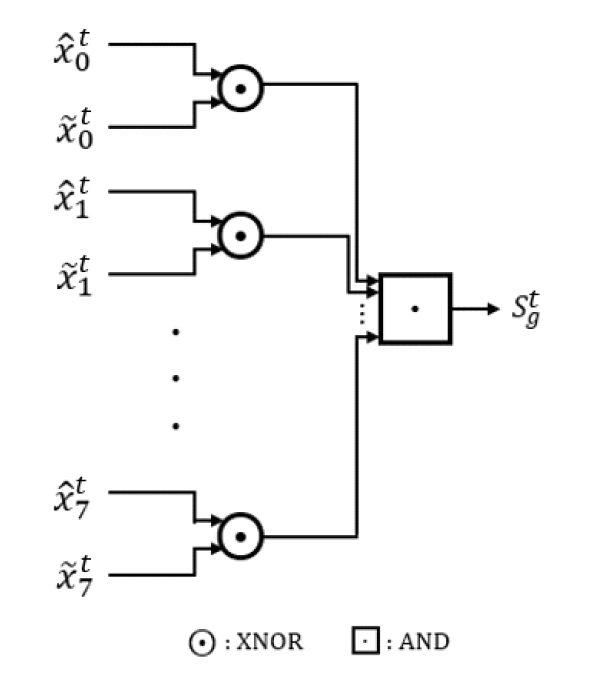
(8)[TeX:] $$\hat{u}_k= \begin{cases}0, & L_{(0, k)}^{I_m}+R_{(0, k)}^{I_m} \geq 0 \\ 1, & L_{(0, k)}^{I_m}+R_{(0, k)}^{I_m}\lt0\end{cases}$$BP 복호 기법은 [TeX:] $$I_m$$이 커질수록 계산 복잡도와 복호 지연시간이 증가하는 단점이 있다. 이러한 문제를 보완하기 위해 [3]에서는 G-행렬 (G-matrix, GM) 방식과 최소 로그 우도 비 (minimum-LLR, ML) 방식을 조기 종료 판별 기법들로 제안하였다. GM 방식은 매 반복 복호 종료 후 (0,k) 노드의 [TeX:] $$L_{(0, k)}^t+R_{(0, k)}^t, 0 \leq k \leq N-1$$ 값으로 경판정 (hard decision)한 비트 [TeX:] $$\hat{u}_{(0, k)}^t \text { 와 } \mathrm{G}_N$$을 이용하여 부호 비트 [TeX:] $$\hat{x}_k^t, 0 \leq k \leq N-1$$를 도출한다. 이를 [TeX:] $$L_{\left(\log _2 N, k\right)}^t+R_{\left(\log _2 N, k\right)}^t,$$ [TeX:] $$0 \leq k \leq N-1$$로 경판정한 비트 [TeX:] $$\tilde{x}_k^t$$들과 비교하여 [TeX:] $$\hat{x}_k^t=\tilde{x}_k^t, 0 \leq k \leq N-1$$를 만족하면 반복 복호를 종료한다. N=8인 경우를 가정하여 GM 기반 조기 종료 판별기의 하드웨어 구조를 도식화하면 그림 4와 같다. 그림 4에서 경판정기 (hard decision block)는 입력이 ‘0’보다 크거나 같은 경우 ‘0’을 출력하고 작은 경우 ‘1’을 출력한다. 출력신호 [TeX:] $$S_g^t$$는 동등 판별기 (equality detector)에서 출력되는 값으로 [TeX:] $$S_g^t=1$$이면 반복 복호를 종료하고 그렇지 않으면 다음 반복 복호를 수행하며 동등 판별기의 구현 구조는 그림 5와 같다. 그림 4와 5를 통해 확인할 수있는 GM 기반 조기 종료 판별기의 구현 복잡도를 요약하면 표 1과 같다. 그림(Fig.) 4. GM 기반 조기 종료 판별기의 하드웨어 구조 (N=8) (Hardware architecture of GM early termination detector (N=8)) 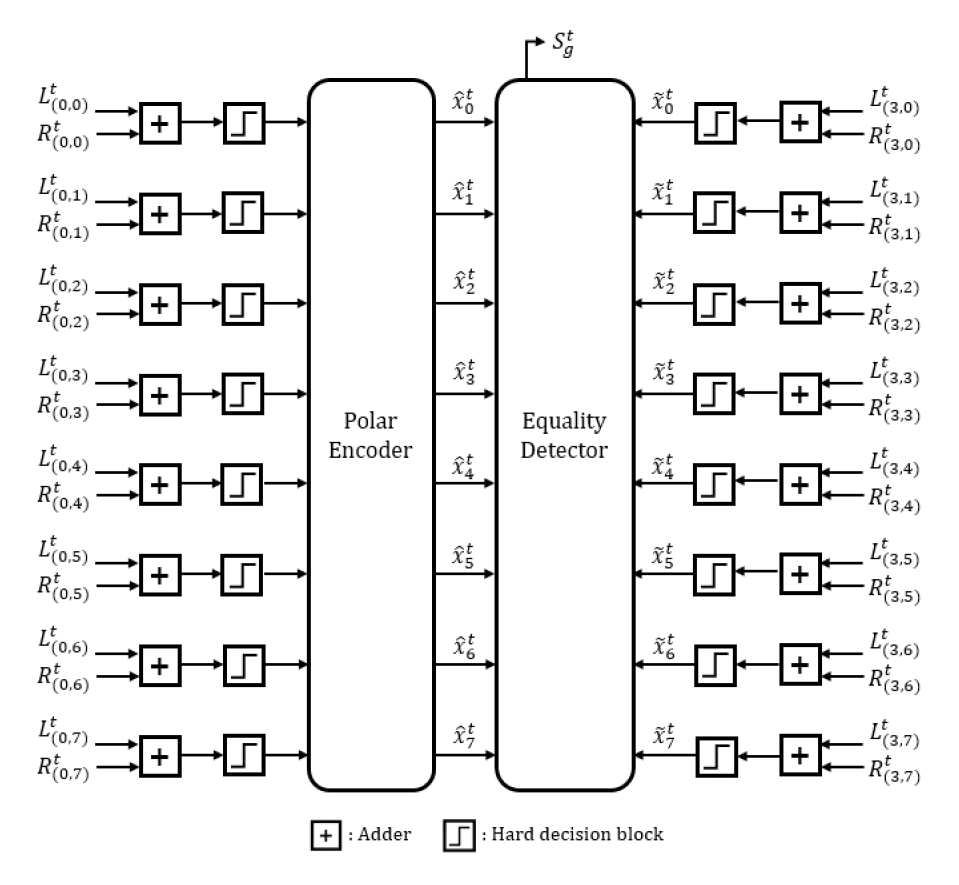 표(Table) 1. GM 기반 조기 종료 판별기 구현 복잡도 (Implementation complexity of GM early termination detectors)
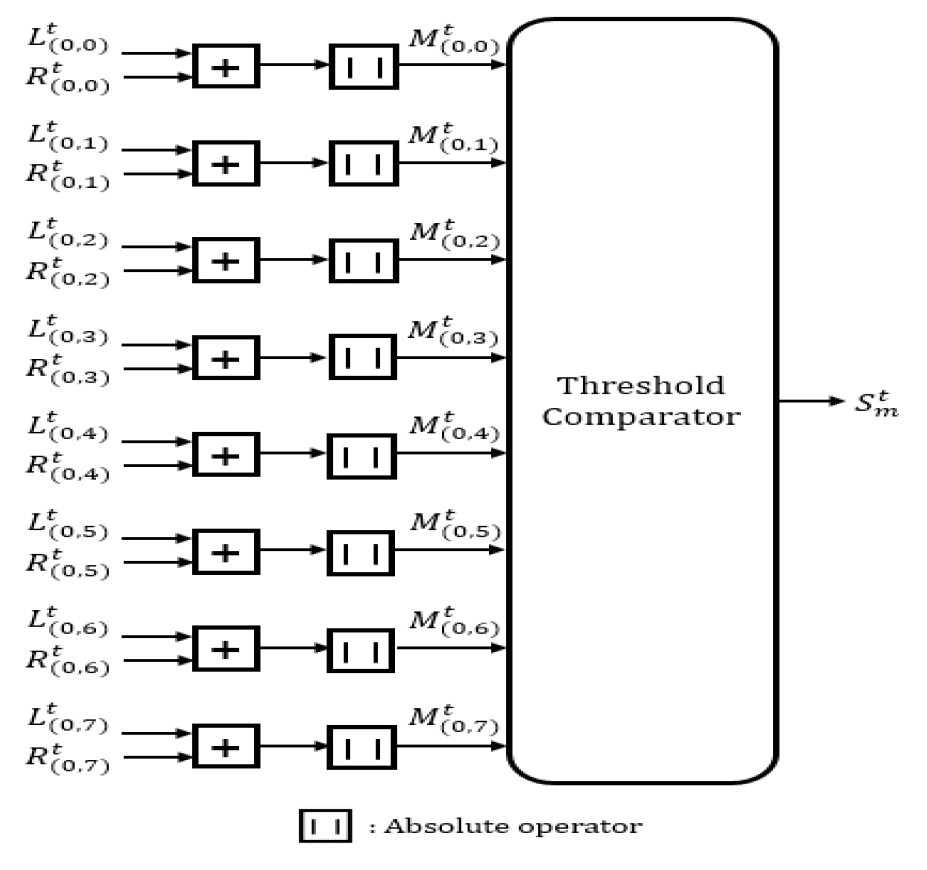
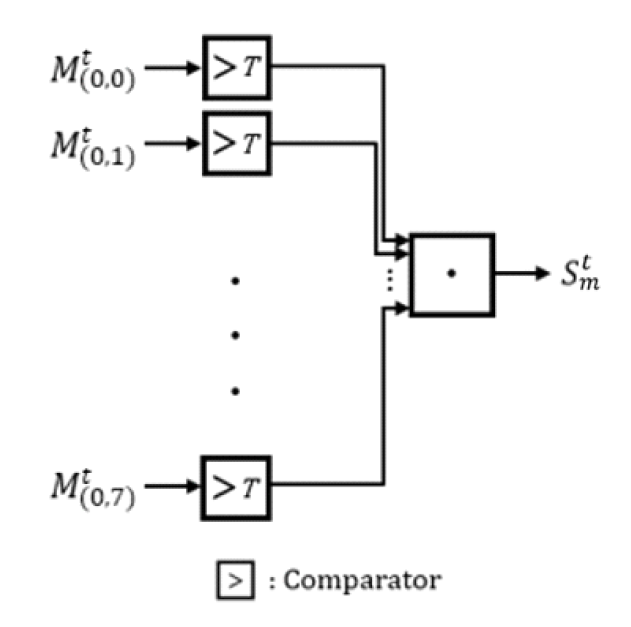
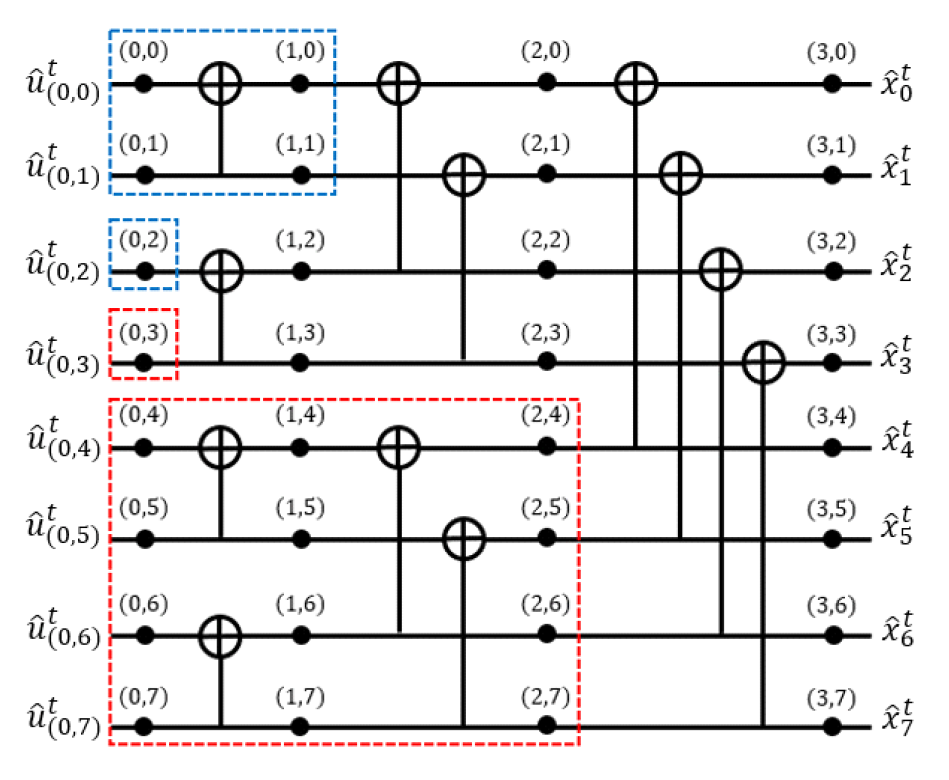
ML 방식은 t번째 반복 복호마다 모든 [TeX:] $$M_{(0, k)}^t=\left|L_{(0, k)}^t+R_{(0, k)}^t\right|, k=0,1, \ldots, N-1$$ 값들이 미리 설정된 임계값 T보다 큰 경우 반복 복호를 종료한다. N=8인 경우를 가정하여 ML 기반 조기 종료 판별기의 하드웨어 구조를 도식화하면 그림 6과 같다. 그림 6에 나타낸 [TeX:] $$S_m^t$$는 t번째 반복 복호마다 임계값 비교기 (threshold comparator)에서 출력되는 신호로 [TeX:] $$S_m^t=1$$이면 반복 복호를 종료하고 그렇지 않으면 다음 반복 복호를 수행한다. 임계값 비교기의 구현 구조를 도식화하면 그림 7과 같다. 여기에서 비교기 (comparator)는 입력이 T보다 큰 경우에는 ‘1’, 그렇지 않은 경우에는 ‘0’을 출력한다. 그림 7과 8을 통해 확인할 수 있는 ML 기반 조기 종료 판별기의 구현 복잡도를 요약하면 표 2와 같다. Ⅲ. 제안하는 기법기존에 제안된 ET-BP 복호기의 조기 종료 판별기는 매 반복 복호 종료 시점마다 동작하며 구현 복잡도가 비교적 높다. 본 논문에서는 극 부호의 임계 집합을 이용한 낮은 복잡도의 조기 종료 판별기들을 제안한다. 길이가 N인 극 부호는 [TeX:] $$N / 2^b, \quad 0 \leq b \leq n$$ 길이를 갖는 여러 개의 하위 극 부호로 나눌 수 있다[4]. 이때 부호율 (code rate) R=1을 만족하며 가장 긴 길이를 갖는 하위 극 부호들을 모두 찾고, 각 하위 극 부호의 첫 번째 비트 인덱스들을 원소로 갖는 임계 집합 C를 생성할 수있다. N=8, K=5이고 I={3,4,5,6,7}인 극 부호의 팩터 그래프를 도식화하면 그림 8과 같다. 하위 극 부호의 입력 비트들의 인덱스들이 I의 원소여서 R=1을 을 만족하며 가장 긴 길이를 갖는 하위 극 부호들을 찾아 적색으로 표시하면 그림 8과 같다. 이때 임계 집합은 C={3,4}이며 이와 유사한 방법으로 R=0을 만족하며 가장 긴 길이를 갖는 하위 극 부호들을 찾아 청색으로 나타내면 그림 8과 같다. 또한, 청색으로 나타낸 하위 극 부호들의 첫 번째 비트 인덱스들을 원소로 갖는 임계 집합은 F={0,2}가 된다. 임계 집합 C의 m번째 원소를 인덱스로 갖는 비트를 포함한 하위 극 부호 입력 비트들의 인덱스 집합을 [TeX:] $$P_m, 1 \leq m \leq o(C)$$로 나타낼 때 [TeX:] $$P_1=\{3\}$$이고 [TeX:] $$P_2=\{4,5,6,7\}$$이다. 식 (4), (5) 및 그림 8을 통해 확인할 수 있는 바와 같이 [TeX:] $$o(\bullet)$$를 집합의 원소 개수로 정의하면 모든 반복 복호 과정에서 [TeX:] $$m=1,2, \ldots, o(C)$$에 대해 식 (9)가 성립한다.
따라서 [TeX:] $$(l, k), \quad 0 \leq l \leq \log _2 O\left(P_m\right), \quad k \in P_m$$노드의 [TeX:] $$L_{(l, k)}^t+R_{(l, k)}^t$$에 대한 경판정 값 [TeX:] $$\hat{u}_{(l, k)}^t \text { 는 } L_{(l, k)}^t$$만으로 계산할 수 있으며 [TeX:] $$\hat{u}_{(0, k)}^t, k \in P_m$$와 생성행렬 [TeX:] $$\mathrm{G}_{o\left(P_m\right)}$$를 이용하여 식 (1)과 같이 극 부호화 결과는 [TeX:] $$\hat{u}_{\left(\log _2 O\left(P_m\right), k\right)}^t,$$ [TeX:] $$k \in P_m$$와 항상 일치한다. 따라서 [TeX:] $$\hat{u}_{(0, k)}^t, k \in P_m$$를 입력 비트로 갖는 하위 극 부호에서는 [TeX:] $$\hat{u}_{\left(\log _2 o\left(P_m\right), k\right)}, k \in P_m$$를 이용하여 조기 종료 판별을 수행하여도 기존 GM 기법과 동일한 결과를 얻을 수 있다. F의 w번째 원소를 인덱스로 갖는 비트를 포함하는 하위 극 부호의 입력 비트 인덱스 집합을 [TeX:] $$U^w,$$[TeX:] $$1 \leq w \leq o(F)$$로 나타내면 [TeX:] $$\hat{u}_{(0, k)}^t, \quad k \in U_w$$들은 고정 비트이므로 해당 하위 극 부호 내의 모든 노드의 로그 우도 비에 대한 경판정 값은 항상 ‘0’이다. 따라서 [TeX:] $$\hat{u}_{(0, k)}^t, \quad k \in U_w$$들이 입력 비트인 하위 극 부호에서는 [TeX:] $$(l, k), l=\log _2 O\left(U_w\right), \quad k \in U_w$$ 노드에 ‘0’을 설정한 후 조기 종료 판별을 수행하여도 기존 GM 기법과 동일한 결과를 얻을 수 있다. 또한, 그림 8에서 [TeX:] $$(l, k), l=\log _2 O\left(U_w\right), \quad k \in U_w$$ 노드들의 경판정 결과는 항상 ‘0’이므로 [TeX:] $$(2, k), 0 \leq k \leq 3$$ 노드의 값은 항상 [TeX:] $$\hat{u}_{(0,3)}$$와 같음을 확인할 수 있다. 이러한 특징들을 이용하여 그림 9와 같은 낮은 복잡도의 GM 기반 조기 종료 판별기를 도출할 수 있다. 그림 9에서 확인할 수 있는 바와 같이 제안하는 GM 기반 조기 종료 판별기는 [TeX:] $$\hat{u}_{(0, k)}^t, k \in P_m$$와 [TeX:] $$\hat{u}_{(0, k)}^t, k \in U_w$$를 입력 비트로 갖는 하위 극 부호들 내에서 수행되는 경판정 및 부호화 과정이 필요하지 않다. 또한, [TeX:] $$(l, k), l=\log _2 O\left(U^w\right), \quad k \in U_w$$ 노드에서의 XOR 연산이 필요하지 않아 기존 GM 기반 조기 종료 판별기 대비 구현 복잡도를 낮출 수 있다. 그림(Fig.) 9. 제안하는 GM 기반 조기 종료 판별기의 하드웨어 구조 (N=8, K=5) (Proposed hardware architecture of the GM early termination detector (N=8, K=5)) 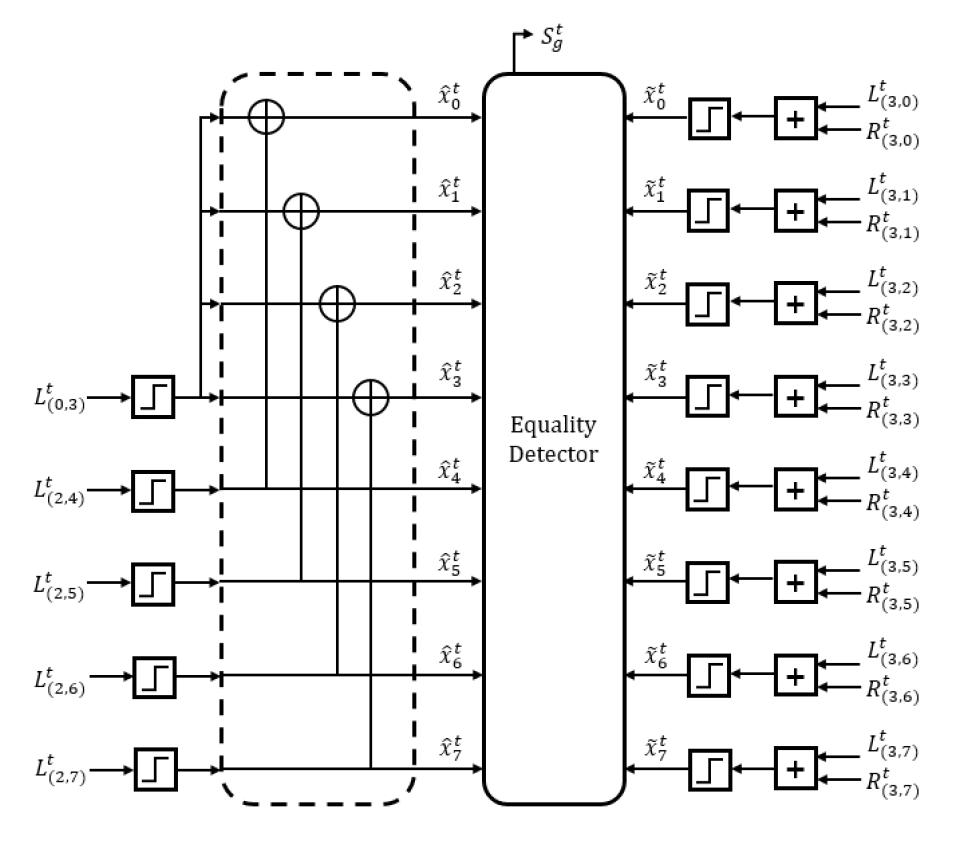 BP 복호에서는 식 (4)와 같이 [TeX:] $$R_{(0, k)}^0=\infty, k \in I_c$$로 설정되며 반복 복호 시 해당 값이 그대로 유지되므로 [TeX:] $$M_{(0, k)}^t, k \in I_c$$은 항상 T보다 크다. 한편, 식 (9)를 통해 확인할 수 있는 바와 같이 [TeX:] $$(0, k), k \in P_m$$ 노드에서의 로그 우도 비는 [TeX:] $$L_{(0, k)}^t$$ 만으로 계산된다. 또한 [TeX:] $$o\left(P_m\right) \geq 2$$인 경우, [TeX:] $$L_{(l, k)}^t, \quad 0 \leq l \leq \log _2 O\left(P_m\right)-1,$$ [TeX:] $$k \in P_m$$은 식 (10)과 같이 계산될 수 있음을 알 수 있다.
(10)[TeX:] $$\begin{aligned} & L_1^{o, t}=f\left(L_1^{i, t}, L_2^{i, t}\right) \\ & L_2^{o, t}=L_2^{i, t} \end{aligned}$$식 (10)을 통해 [TeX:] $$o\left(P_m\right) \geq 2, m=0,1, \ldots, o(C)$$인 하위 극 부호에서 가장 첫 번째 입력 비트의 로그 우도 비는 [TeX:] $$L_{\left(\log _2 o\left(P_m\right), k\right)}^t, k \in P_m$$들의 [TeX:] $$f(\bullet)$$ 연산으로만 계산됨을 확인할 수 있으며 식 (6)을 통해 [TeX:] $$f(\bullet)$$는 식 (11)을 만족함을 확인할 수 있다.
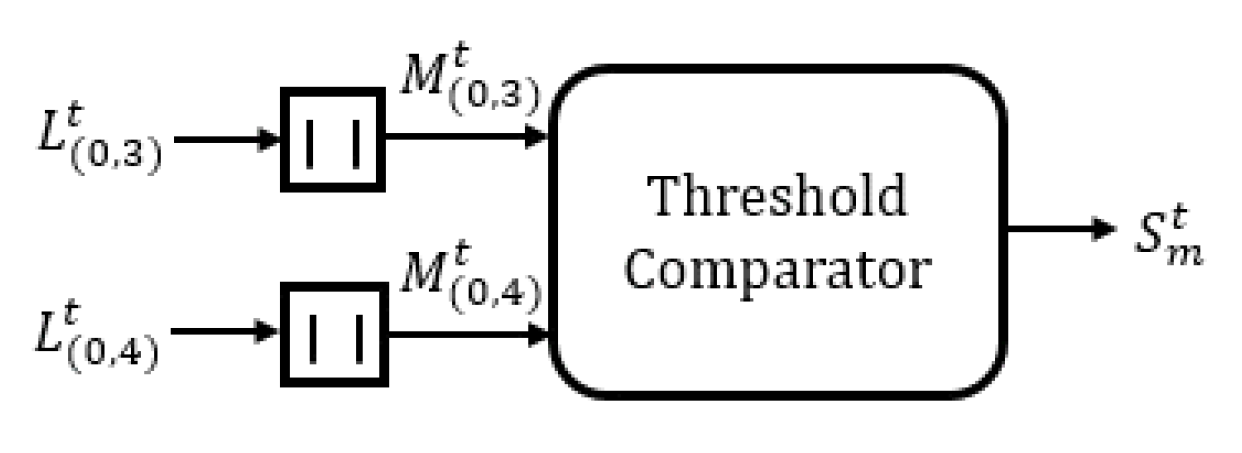
따라서 [TeX:] $$\hat{u}_{(0, k)}^t, \quad k \in P_m$$들을 입력 비트로 갖는 각 하위 극 부호에서는 C의 원소 중 하나를 인덱스로 갖는 가장 첫 번째 입력 비트의 로그 욷 비 절대값이 항상 가장 작은 값을 갖는다. 이러한 특징으로 인하여 [TeX:] $$L_{(0, k)}^t, k \in C$$ 값들만으로 ML 기반 조기 종료 판별을 수행하여도 기존 ML 기반 조기 종료 판별기와 동일한 성능을 보이므로 그림 10과 같은 ML 기반 조기 종료 판별기를 도출할 수 있다. 그림 10에서 확인할 수 있는 바와 같이 제안하는 판별기는 [TeX:] $$L_{(0, k)}^t, k \in C$$로만 조기 종료 여부가 판별되므로 기존 판별기 대비 구현 복잡도를 크게 낮출 수 있다. Ⅳ. 전산실험 결과제안하는 조기 종료 판별기들을 적용한 ET-BP 복호기의 성능 확인을 위한 전산실험 파라미터는 표 3과 같다. 본 논문에서는 극 부호 설계에 β-expansion[7,8] 기법을 사용하였다. 표 3에서 T로 설정한 값은 [TeX:] $$\hat{u}_k$$ ‘0’ 또는 ‘1’일 확률이 각각 99.9%일 때의 로그 우도 비 절대값에 해당하며 [TeX:] $$I_m$$은 BP 복호 기법에서 더 이상의 성능개선이 이루어지지 않는 최소값으로 설정하였다. ET-BP 복호 시 GM 및 ML 기반 조기 종료 기법을 사용하였을 때 제안하는 기법의 프레임 오류율 성능을 각각 그림 11과 12에 나타내었다. 또한, 기존 기법과 제안하는 기법의 평균 반복 복호 수를 그림 13에 나타내었다. 그림 11-13을 통해 제안하는 판별기를 사용하여도 매 반복 복호마다 기존 판별기와 동일한 복호 성능 및 판별 결과를 도출할 수 있어 프레임 오율 성능과 평균 반복 복호 수가 기존 판별기와 동일함을 확인할 수 있다. 표(Table) 3. 전산실험 파라미터 (simulation parameters)
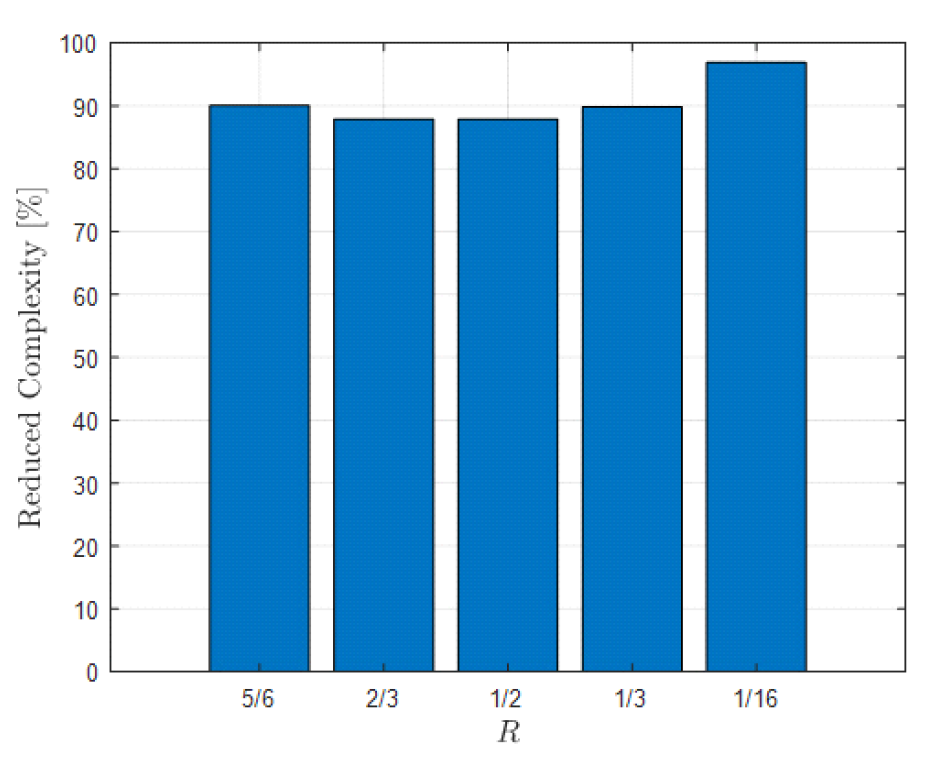
그림(Fig.) 11. 판별기에 따른 ET-BP 복호 기법의 프레임 오율 성능 (GM) (FER performance of ET-BP decoding scheme according to detector (GM)) 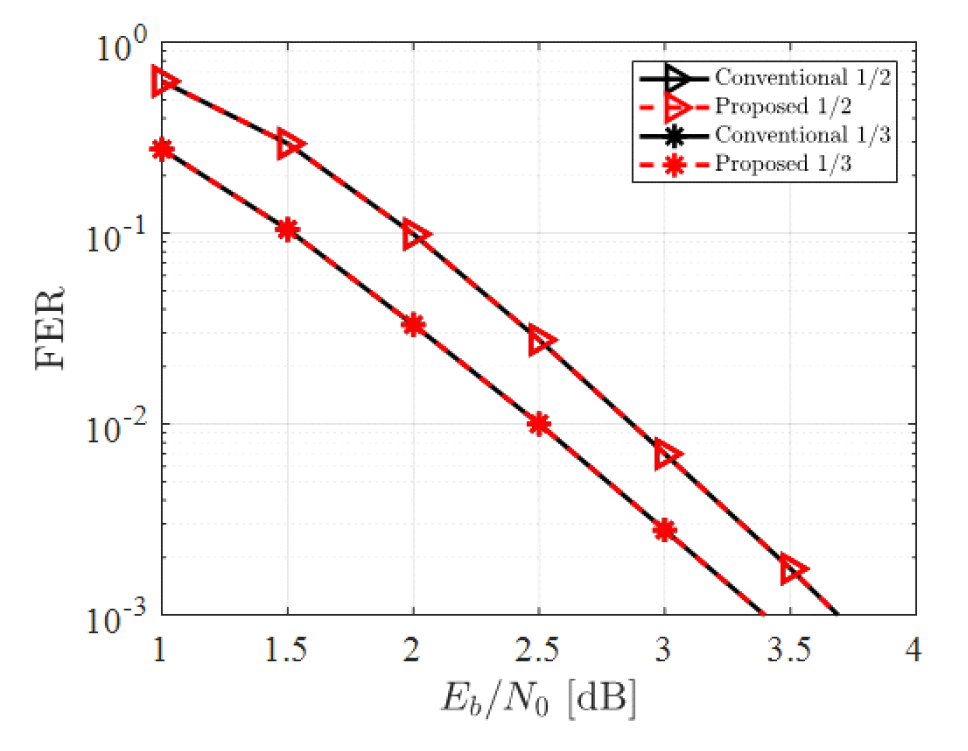 그림(Fig.) 12. 판별기에 따른 ET-BP 복호 기법의 프레임 오율 성능 (ML) (FER performance of ET-BP decoding scheme according to detector (ML)) 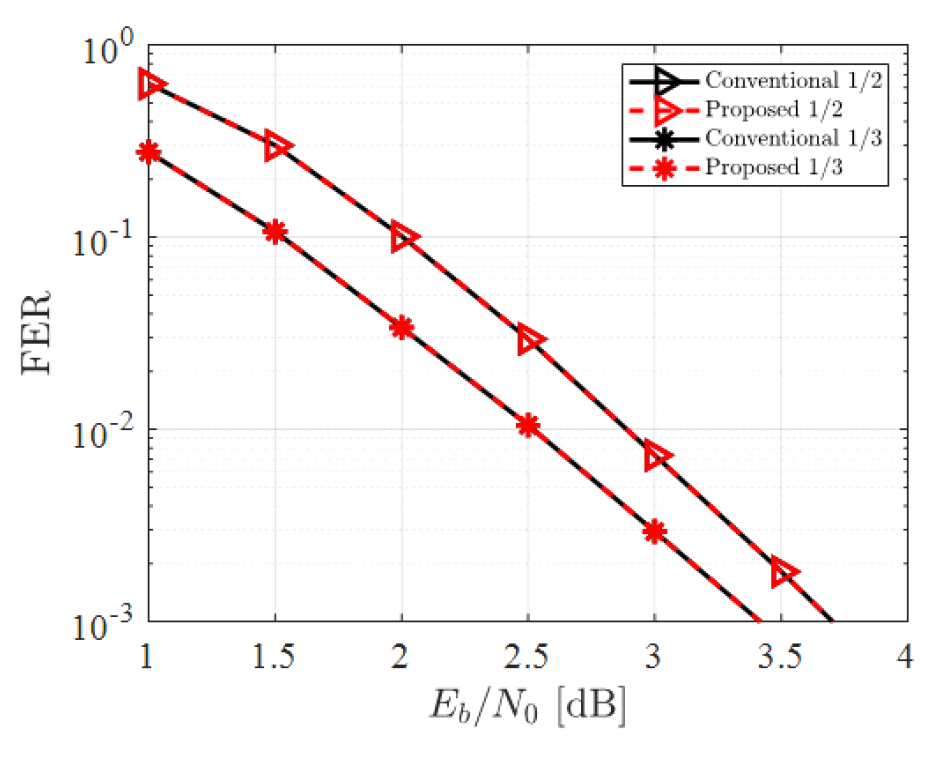 그림(Fig.) 13. 판별기에 따른 ET-BP 복호 기법의 평균 반복 복호 수 (Average number of iterations of ET-BP decoding scheme according to detector) 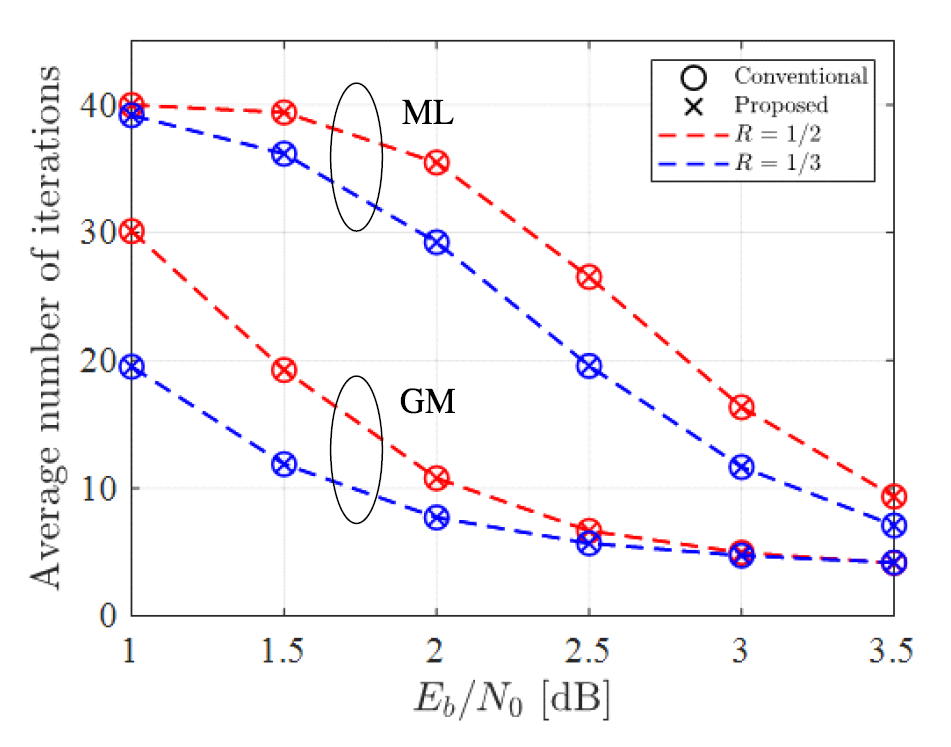 제안하는 GM 기반 조기 종료 판별기에 요구되는 구현 복잡도를 기존 판별기와 비교하였으며 그 결과를 표 4에 나타내었다. 표 4에서 확인할 수 있는 바와 같이 제안하는 조기 종료 판별기의 경우 기존 판별기 대비 덧셈 복잡도는 1/2로, 경판정 복잡도는 (N+K)/2N로 각각 감소한다. 제안하는 판별기에서 요구되는 XOR 연산 복잡도는 R에 따라 달라진다. 상용 통신 시스템들에서 자주 사용되는 R[9,10]들에 대해 기존 판별기 대비 제안하는 판별기의 XOR 연산 복잡도 감소율을 확인하였으며 이를 그림 14에 나타내었다. 그림 14에서 확인할 수 있는 바와 같이 제안하는 GM 기반 판별기를 사용함으로써 요구되는 XOR 연산 복잡도를 최대 81.1% 줄일 수 있다. 표(Table) 4. 기존 및 제안하는 GM 기반 조기 종료 판별기 구현 복잡도 (Implementation complexity of the conventional and proposed GM early termination detectors)
그림(Fig.) 14. 기존 판별기 대비 XOR 연산 복잡도 감소량 [%] (Reduction in XOR operation complexity compared to the original detector [%]) 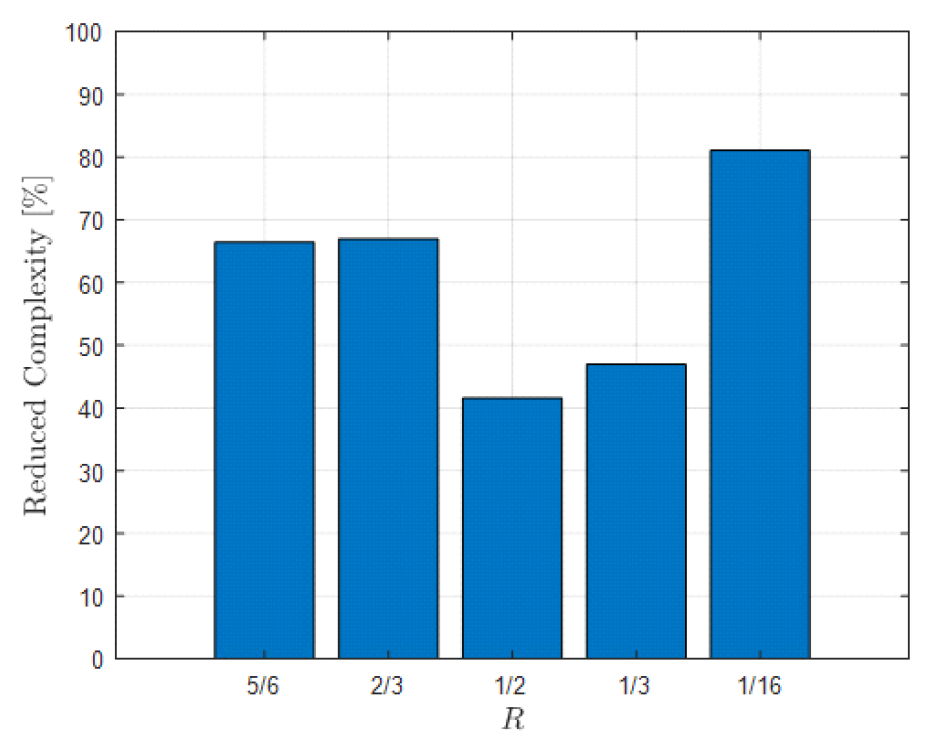 제안하는 ML 기반 조기 종료 판별기의 구현 복잡도를 기존 기법과 비교하였으며 그 결과는 표 5와 같다. 표 5에서 확인할 수 있는 바와 같이 제안하는 판별기의 경우 덧셈기는 필요치 않으며 절댓값 및 비교기 연산 복잡도 감소율은 R에 따라 달라 R에 따른 복잡도 감소율을 그림 15에 나타내었다. 그림 15에서 확인할 수 있는 바와 같이 제안하는 판별기는 덧셈 연산이 전혀 필요하지 않을 뿐만 아니라 절댓값 및 비교 연산 복잡도 역시 고려한 모든 부호율에 대해 최소 87.9%부터 최대 96.9%만큼 줄일 수 있어 ML 기반 조기 종료 판별기 구현에 요구되는 복잡도를 크게 낮출 수 있다. Ⅴ. 결 론극 부호의 복호를 위해 ET-BP 복호를 사용할 경우 기존의 BP 복호 기법대비 계산 복잡도 및 복호 지연시간이 줄지만 조기 종료 여부 판별을 위한 별도의 하드웨어가 요구된다. 본 논문에서는 낮은 복잡도를 갖는 조기 종료 판별기들을 제안하였다. 제안하는 판별기들은 BP 복호기 내에서 각 노드별로 계산되는 로그 우도 비의 특징들을 활용하여 기존 조기 종료 판별기들과 동일한 성능을 유지하면서 구현 복잡도를 크게 낮출 수 있다. 향후 본 논문에서 제안한 판별기에 최적화된 복호 기법을 도출함으로써 ET-BP 복호기에 요구되는 복잡도를 추가로 낮출 수 있을 것으로 예상하며 이에 관한 연구가 필요하다. BiographyBiographyBiographyReferences
|
StatisticsCite this articleIEEE StyleC. Lee, S. Back, C. Park, W. Oh, "Low Complexity Early Termination Detector for Polar Code Belief Propagation Decoding," The Journal of Korean Institute of Communications and Information Sciences, vol. 49, no. 3, pp. 435-443, 2024. DOI: 10.7840/kics.2024.49.3.435.
ACM Style Chungsu Lee, Sungyeol Back, Chansoo Park, and Wangrok Oh. 2024. Low Complexity Early Termination Detector for Polar Code Belief Propagation Decoding. The Journal of Korean Institute of Communications and Information Sciences, 49, 3, (2024), 435-443. DOI: 10.7840/kics.2024.49.3.435.
KICS Style Chungsu Lee, Sungyeol Back, Chansoo Park, Wangrok Oh, "Low Complexity Early Termination Detector for Polar Code Belief Propagation Decoding," The Journal of Korean Institute of Communications and Information Sciences, vol. 49, no. 3, pp. 435-443, 3. 2024. (https://doi.org/10.7840/kics.2024.49.3.435)
|