IndexFiguresTables |
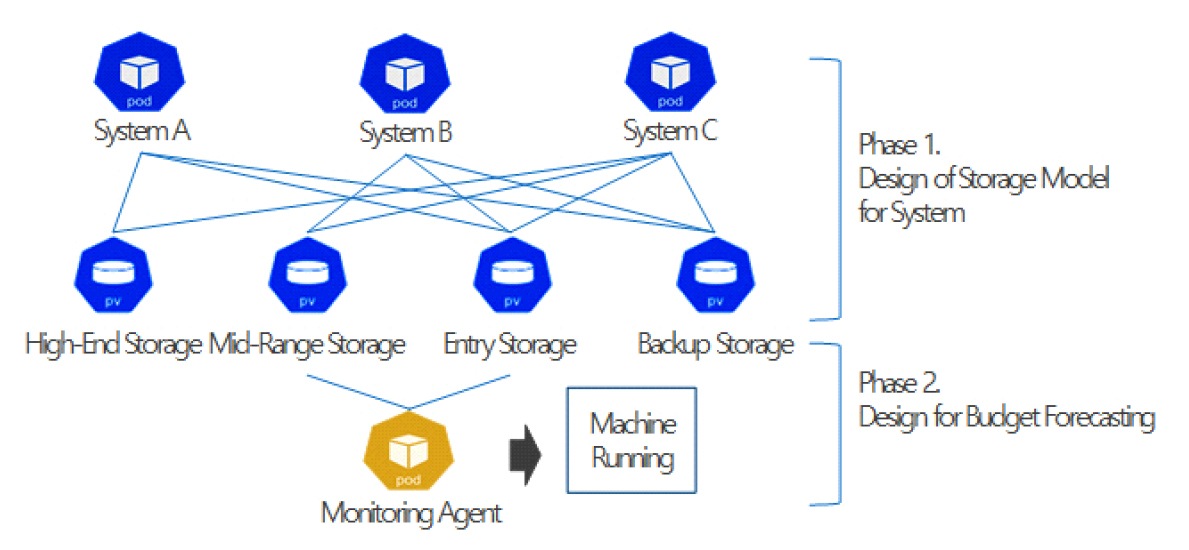
Sun-chul Park and Young-han KimDesign of a Storage Service Operation Model for Cloud Service Cost ReductionAbstract: As cloud adoption proliferates and operational costs increase, interest in Finance and DevOps(FinOps) for cost management is growing. Existing studies have focused on reducing storage costs through techniques such as remote relocation and compression, but simple optimization is limited as data and inter-dependencies increase. This study proposes a hierarchical storage deployment model that uses the services of a single cloud service provider(CSP) optimized for a 3-tier system consistring of WEB, WAS, and DB components. This model shows 56% annual cost reduction compared to a single model approach. Recurrent Neural Network (RNN)-based Long Short-Term Memory (LSTM) machine learning predicts budget overruns with an error rate of 18%. This study supports cost reduction and effective FinOps in cloud operations. Keywords: Cloud Cost Optimizing , Cloud Storage Model , FinOps , RNN , LSTM Ⅰ. 서 론기존 시스템의 클라우드 전환 가속화에 따라 클라우드 사용비용이 새로운 문제가 되고 있다. 사용비용은 관리하지 않으면 예산초과로 문제가 되어 기업의 클라우드 지속 가능성을 위협하게 되었고, IT 부서는 비용관리가 높은 우선순위의 업무가 되었다[1]. 이러한 원인으로 인해 비용문제를 전사적으로 통합 관리하는 체계인 핀옵스(FinOps: Finance and DevOps) 활용도도 증가하고 있으며, 클라우드 서비스(CSP: Cloud Service Provider)도 핀옵스 관련 지원기능을 강화하고 있다[2]. L. M. Gutta의 클라우드 자원의 총소유비용(TCO: Total Cost of Ownership) 조사분석 연구에서 가장 TCO가 높은 자원은 스토리지로 평가 되었다[3]. 스토리지는 다른 컴퓨팅 자원과 다르게 운영시 데이터가 누적되어 증가하는 특성이 있다. 일반적인 클라우드 비용연구는 소유와 사용의 비용 차이에 포커스하고 있다. K. H. Kim et al.은 사용비용의 경제성분석 연구를 수행하였는데[4], 마이그레이션 관점만 고려한 정적분석에 그친 점은 아쉽다. 특히, 스토리지 사용비용 최적화 연구는 주로 멀티클라우드 요금차이를 이용한 최적화 방안을 제시하지만, 실무적 관점에서는 운영복잡도 증가, 지연 문제 등으로 실시간 서비스에는 적용이 어렵다. 따라서, 본 연구는 단일 CSP에서 비용 최적화를 달성하는 모델을 제안하여 실무 적용성을 높였다. 실시간 서비스의 스토리지 데이터는 지속 누적 증가하는 특성으로 인해 시간이 지날수록 고비용의 직접적인 요인이 된다. 이러한 이유로 스토리지는 초기 장기적 관점의 운영 배치설계가 매우 중요하다. 본 논문은 실시간 서비스의 데이터 용도에 맞추어 단일 CSP 내에서 복합 배치모델을 통한 비용 최적화를 연구한다. 실시간 서비스에서 발생하는 데이터의 특성과 CSP의 스토리지 비용 계층을 연관 지어 분석하고, 클라우드 네이티브에 적합한 배치모델을 제안한다. 또한, 장기 미참조 데이터를 재배치하여 비용효과를 향상시키고, 비주기적인 이벤트 변화로 인한 비용증가도 포함하여 예측할 수 있도록 머신러닝을 통해 핀옵스를 지원한다. 성능시험은 중대형 규모의 기존 시스템의 스토리지 데이터를 클라우드로 전환 후 운영할 때의 비용을 시뮬레이션하여 제안모델의 효용성을 증명한다. 논문구성은 서론에 이어 2장에서는 클라우드 비용 최적화와 관련된 선행연구에 대해 살펴보며, 3장에서는 제안기법을 상세히 설명하고 4장에서는 구현 및 실험 평가 내용을 정리 후 마지막으로 5장에서 결론을 제시한다. Ⅱ. 관련 연구클라우드 스토리지 비용연구는 대부분 데이터 보존 비용 연구가 다수이다. M. Liu et al.은 사용자 관점에서의 클라우드 스토리지 비용 최적화 관련 연구를 수행하였으나[5], 구체적인 방안없이 가능한 최적화 저장기술을 분류하는 것으로만 그친 것은 아쉬운 점이다. H. Yerramsetty는 클라우드 네이티브를 위한 최적화 연구에서 스토리지 데이터에 수명관리 적용, 스토리지 비용 계층 적용, 데이터 중복제거 적용 등의 방안을 제시하였으나[6], 구체적인 방안으로 주기적 감사와 삭제 같은 비기술적인 권고로만 그친 점은 아쉽다. V. L. Latha et al.은 멀티 클라우드 환경에서 주성분 분석 및 파레토 최적화 기법을 이용한 데이터 배치 최적화를 연구하였다[7]. 연구는 가용성과 재배치 비용만을 고려하고 저장 비용 고려는 제외되었다. Y. Mansouri et al.은 클라우드센터 간의 원격복제로 저장비용과 통신비용을 고려한 최적의 저장소 선정 연구를 수행하였다[8]. 이 연구는 CSP의 대륙 센터간의 원격복제 연구로, 저장비용이 유사하고 오히려 전송비용이 추가되어 효과가 낮다. P. Wang et al.은 멀티 클라우드 스토리지 서비스를 이용하여 고가용성을 위한 비용 최적화 모델을 연구하였다[9]. 여러 법칙을 이용하여 모델을 정의하였으나 실시간 데이터에 대한 고려가 없는 점은 아쉽다. S. Raut et al.은 데이터를 3가지 유형으로 분류하고 비용 예측을 수행하는 정책을 연구하였다[10]. 하지만 대상을 백업 데이터로 한정하고 단순 증가율을 적용하여 전송 패킷에 대한 고려가 부족한 점은 아쉽다. W. Tian et al.은 클라우드 자원별로 스케쥴링을 이용해 확장, 축소로 비용최적화 달성을 제안하였다[11]. 하지만, 스토리지는 다른 자원과 다르게 단순 알고리즘만 제시된 점은 아쉽다. A. K. Y. Yanamala는 압축기법을 이용한 저장용량 축소 방식에 관해 연구하였다. 단순 압축과 중복제거 방식, SSD 스토리지, 하이브리드 스토리지의 최적화 비교 연구를 하였다[12]. 연구는 하드웨어 의존도가 높아 퍼블릭 클라우드에는 적용할 수 없는 한계가 있다. X. Qiu et al.은 파일의 분산을 통해 저비용의 저장소를 사용하는 연구를 수행하였다[13]. 하지만, 하이브리드 방식의 구매비용이 고려되지 않아 아쉽다. P. Waibel et al.은 클라우드 스토리지의 저장모델 활용 최적화 연구를 수행하였으나[14], 연구의 최적화 방식을 단순 저장만을 고려한 점은 아쉽다. Y. Mansouri et al.은 Hot과 Cold 스토리지 계층을 이용해 빈도에 따라 계층을 이동하는 최적화를 연구했다[15]. 하지만, 요청시 계층을 옮기는 등 실시간 성에 대한 고려가 부족하다. A. Q. Khan et al.은 빈도를 기준으로 스토리지 계층을 평가하는 최적화 연구를 수행하였다[16]. 하지만, 평가 요소를 접근빈도로 구분하고, 서비스 파일을 빈도가 낮은 로그파일로만 한정한 점은 아쉽다고 하겠다. 이렇듯 기존의 연구는 스토리지의 장기저장 데이터의 보존비용 최적화가 중심이다. 이와 다르게 본 연구는 실시간성 서비스 데이터의 유형에 따른 저장비용 최적화를 중심으로 한다. Ⅲ. 제안 기법3.1 연구방법본 연구는 실시간 서비스의 유관 데이터의 스토리지 비용 최적화를 연구한다. 기존 시스템의 서비스 과정에서 발생하는 저장 데이터의 분류를 수행한 후 유형에 따른 최적의 클라우드 스토리지 서비스 배치모델을 정의한다. 그림 1은 제안시스템의 목표 모델이다. 연구의 1단계는 시스템 유형에 맞춘 다중 스토리지 배포 모델을 정의한다. 세부적으로는 a. 기존 시스템에서 사용되는 데이터 종류 정의, b. 데이터 특성 분류, c. 스토리지 유형 분류, d. CSP의 스토리지 서비스 계층 특성 분류, e. 클라우드 네이티브 서비스 유형에 맞춘 스토리지 서비스 복합모델 정의 순으로 수행한다. 2단계는 스토리지 비용예산을 예측하도록 구성한다. 본 연구에서는 데이터의 수명, 빈도, 성능 등의 특성에 따라 CSP의 스토리지 서비스를 조합하여 저장하는 모델을 복합 배치모델이라 한다. 복합 배치모델은 각 데이터 유형에 적합한 스토리지 서비스를 식별하여 배치하는 것을 목표로 하며, 이를 기반으로 시스템 구성 단계에서는 다중 스토리지 배치모델로 구현된다. 다음 절에서는 모델을 구성하는 데이터 특성과 스토리지 유형에 대한 분석을 상세히 설명한다. 3.3 스토리지 유형기존 인프라 환경은 물리 스토리지 장비를 사용한다. 표 1은 상용 스토리지 장비 분류이다. 스토리지는 고성능, 고용량일수록 고가장비로 DB 저장은 고성능급 스토리지를, 일반 용도로는 중성능~저성능급 스토리지 장비를 사용한다. 표(Table) 1. 스토리지 하드웨어 분류 (Classification of Storage Hardware)
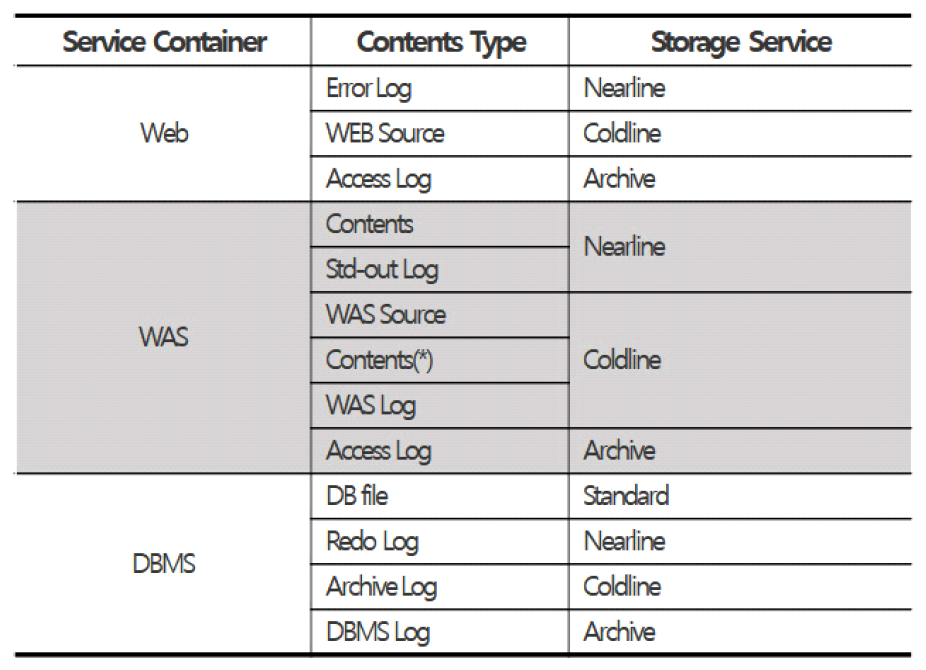
CSP도 물리환경과 유사한 스토리지 계층 서비스를 제공한다. 표 2는 구글(Google)에서 제공하는 스토리지 서비스의 분류이다[17]. CSP는 성능과 고가용성을 기준으로 차등 비용을 적용하는 계층형 스토리지 서비스를 제공하고 있다. 핀옵스 재단의 State of FinOps Report 2023에 따르면, 글로벌 클라우드 시장에서 AWS와 Azure가 가장 높은 시장 점유율을 유지하고, Google은 상위 3대 클라우드 제공업체로서 중요한 위치를 차지하고 있다 하였다. 이 보고서는 Google의 데이터 분석 및 머신러닝 역량과 타 CSP 대비 경쟁력 있는 스토리지 요금 정책을 기반으로 실무 현장에서 자주 채택된다고 강조하고 있다. 또한, A. Q. Khan et al.의 연구에서는 3개사의 스토리지 계층 및 특성을 비교·분석하여 등급을 정의하였으며, 그 결과 구글이 스토리지 저장 비용 측면에서 가장 경쟁력이 높은 것으로 보고하였다[18]. 국내에서는 공공기관, 대기업은 보안인증 등으로 AWS나 Azure를 선호하는 경향이 있으며, IT서비스 중심 기업 일부는 구글을 채택하고 있다. 또한 AWS는 6종류의 스토리지 유형을 제공하는 데 비하여, 구글은 4종류의 계층 서비스를 제공하여 기존 아키텍처와 맵핑 분석이 용이한 장점이 있다. 이에 본 연구는 구글을 기준으로 실험을 수행하였으며, 향후 AWS 및 Azure와의 비교 검증을 통해 연구의 범위를 확장할 예정이다. 표(Table) 2. 구글 클라우드 스토리지 서비스 분류 (Classification of Storage Service by Google)
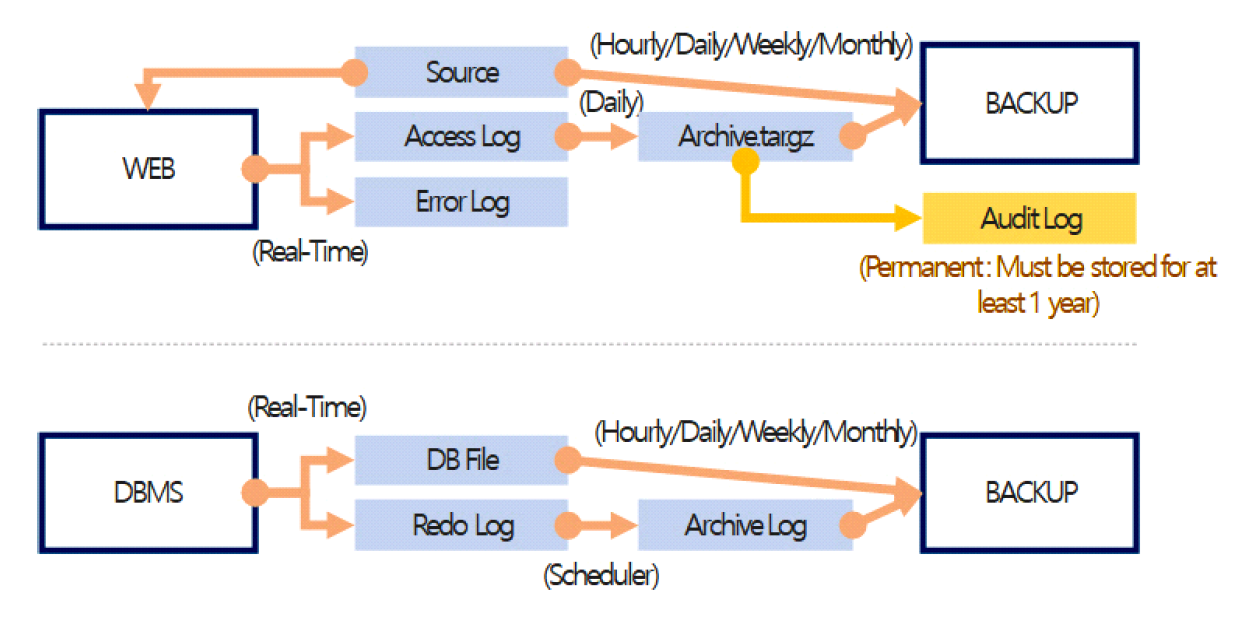
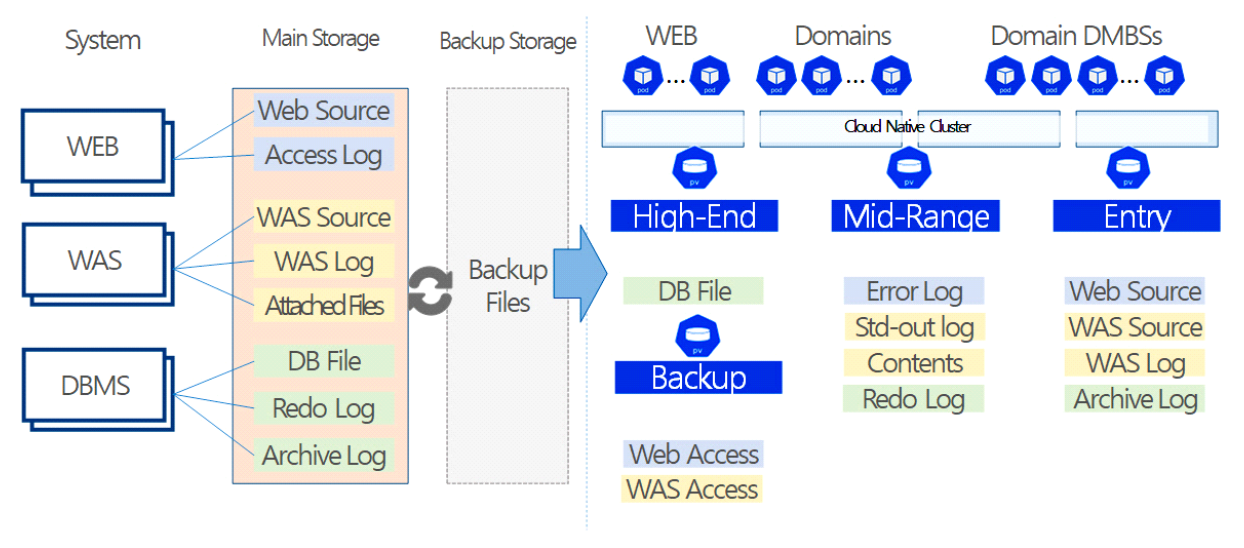
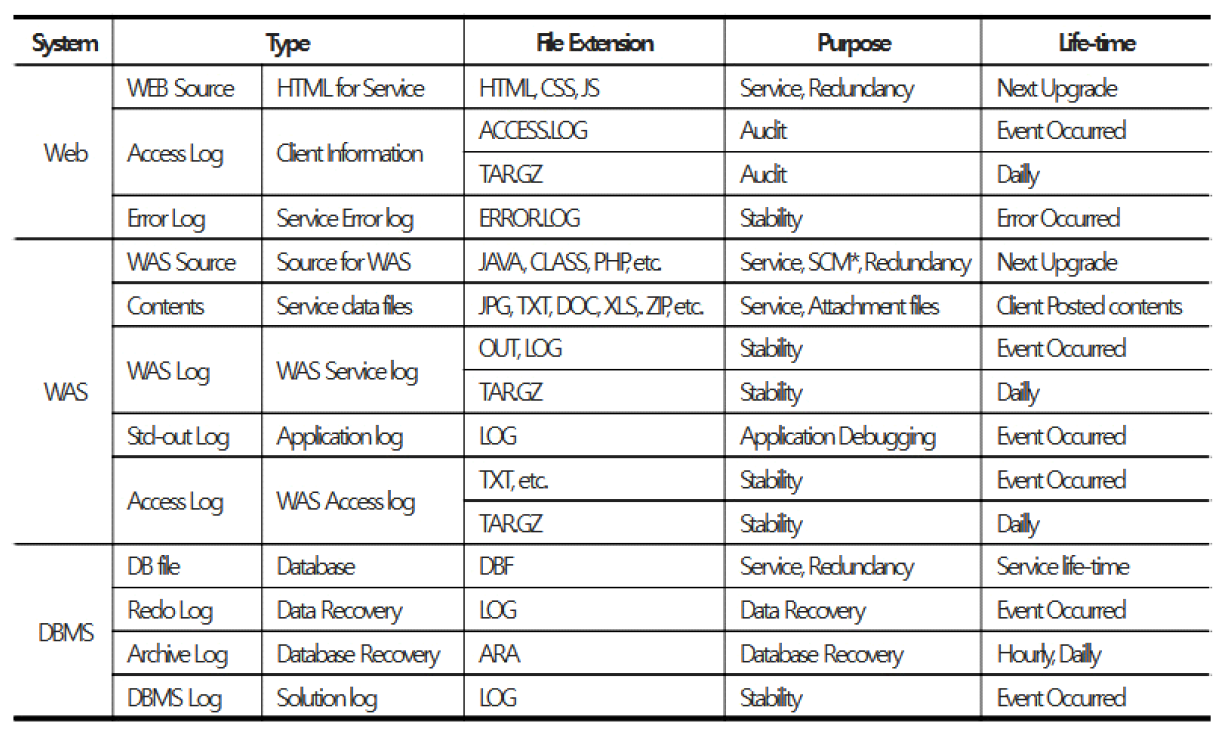
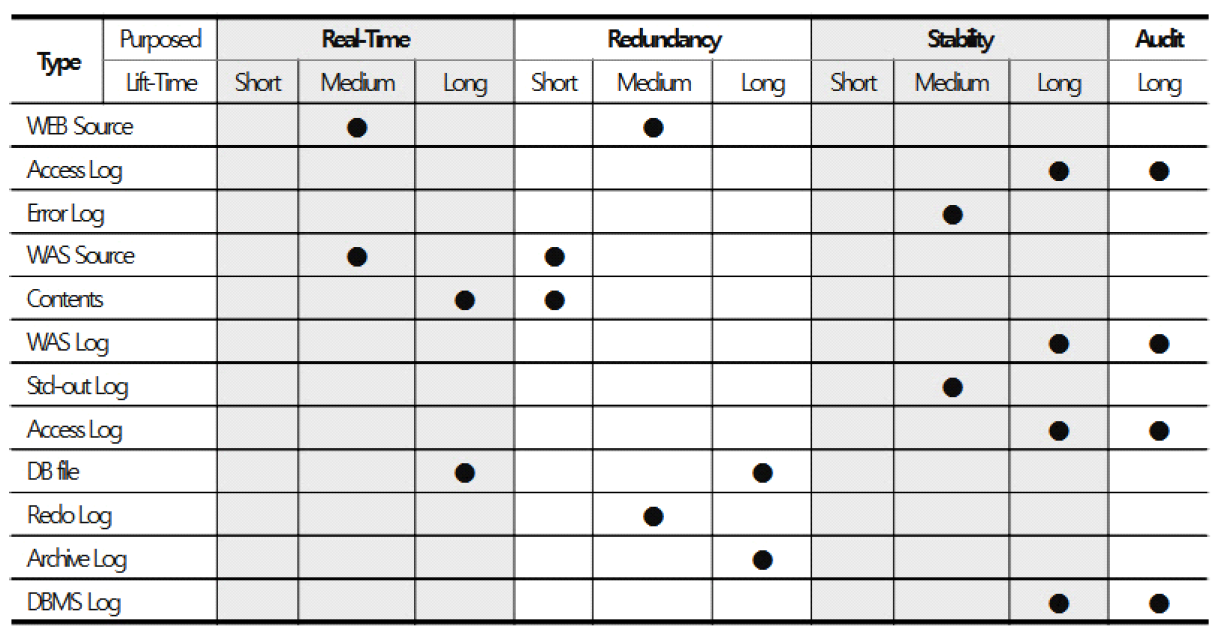
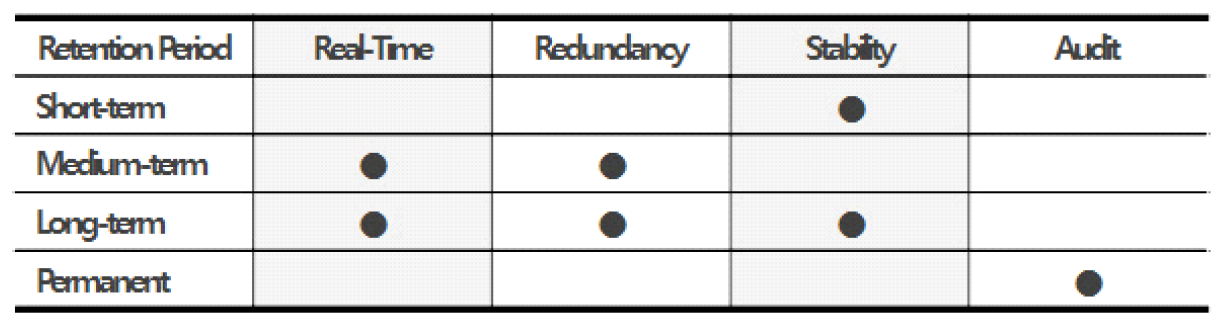
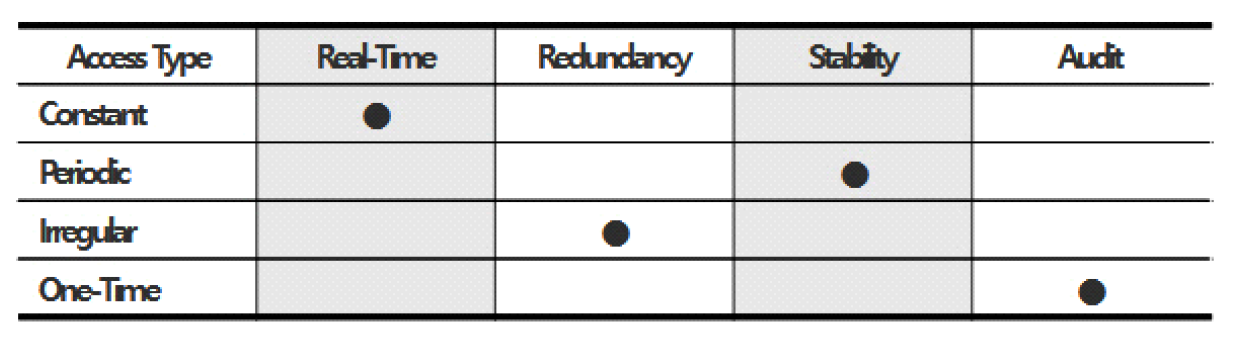
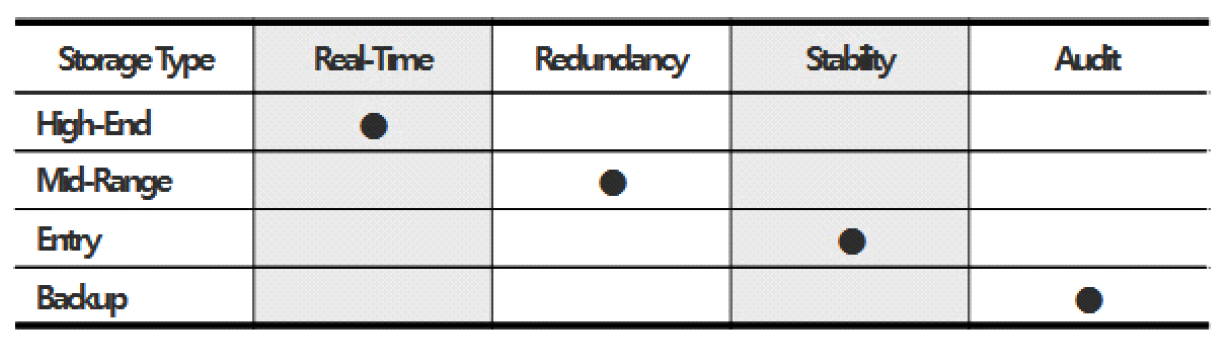
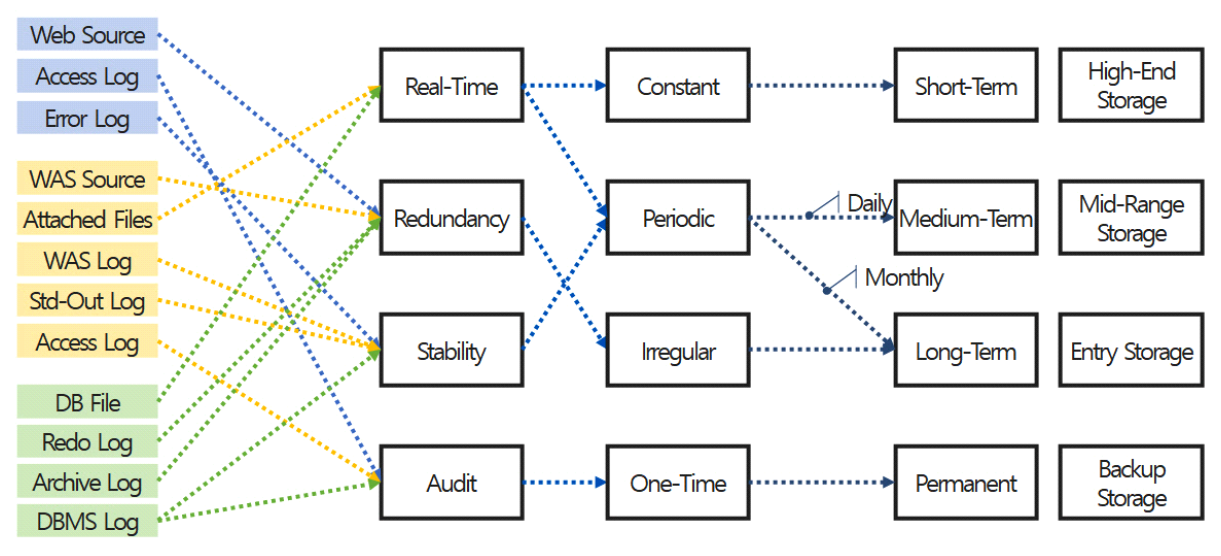
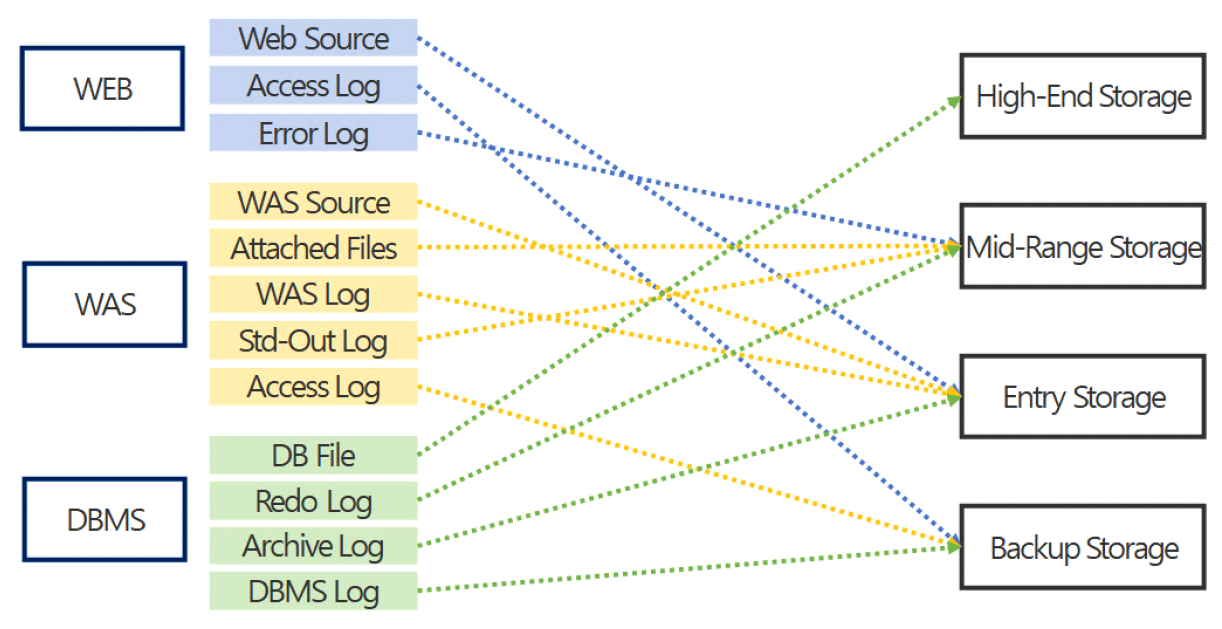
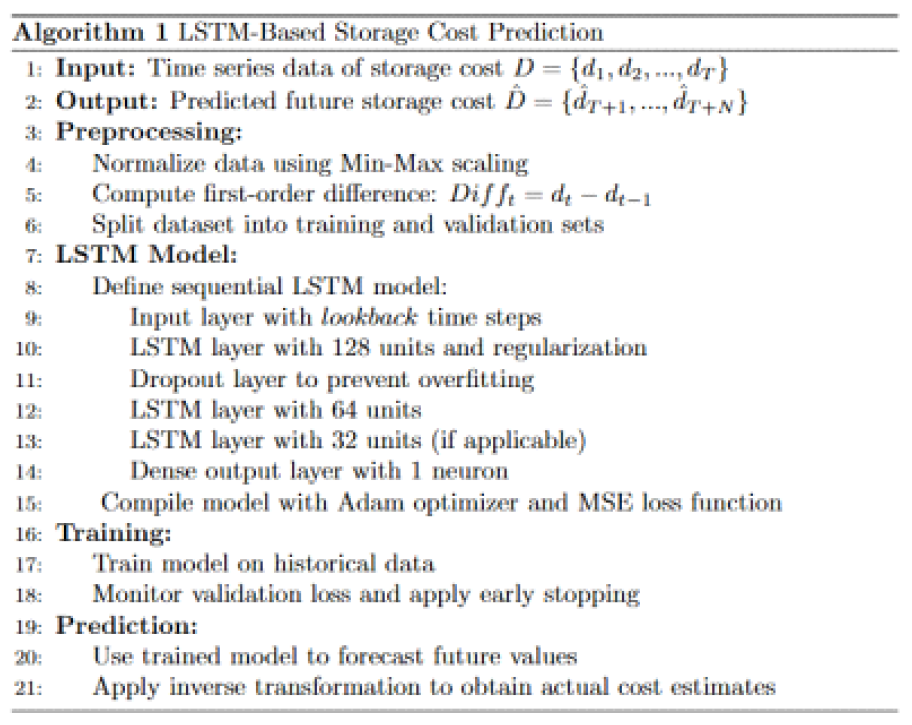
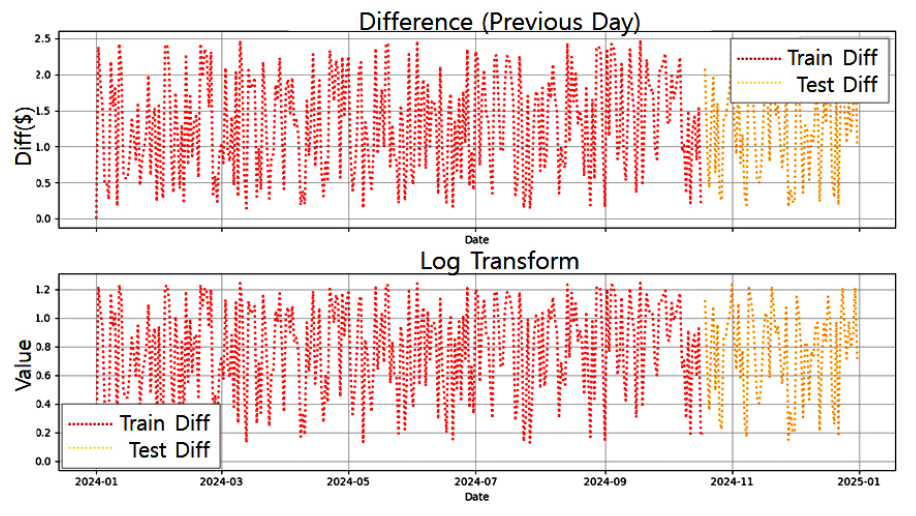
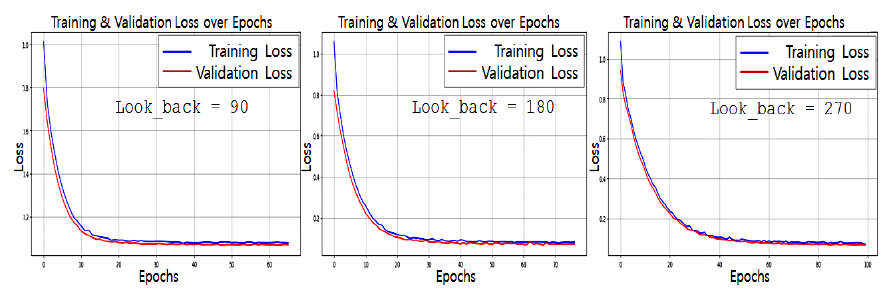
3.4 다중 스토리지 배치 모델그림 3은 기존 시스템 인프라 환경에서의 스토리지 사용 모델이다. 시스템별로 서비스 데이터와 자체생산 데이터를 스토리지에 저장한다. 클라우드 네이티브 환경에서도 물리환경과 유사하게 스토리지 서비스를 영구볼륨으로 컨테이너에 할당한다. 본 연구는 서비스 생명주기 동안 발생하는 데이터 유형에 따른 스토리지 서비스를 식별하고, 컨테이너에 최적의 스토리지 서비스를 복합 배치하는 모델을 설계한다. 그림 4는 복합모델을 위한 분석 절차이다. 서비스 관련 데이터를 명세화한 후 수명, 기간, 빈도, 성능 특성으로 분석하여 적합한 스토리지를 도출한다. 그림 5는 웹 기반 서비스에서 사용되는 서비스 데이터와 자체생산 데이터를 분석한 명세이다. 웹서비스를 구성하는 3계층 시스템별로 관련 데이터의 유형과 확장자, 용도, 수명에 대하여 분석한다. 분석을 통해 스토리지의 특성을 실시간, 연속성용, 안정성용, 감사용의 4가지로 분류하고, 그림 6처럼 세부적 데이터 수명을 단기, 중기, 장기의 3가지 유형으로 분류한다. 수명에 의한 분류를 기간별로 취합하여 분석하면 그림 7과 같다. 각 저장기한은 CSP의 권고에 따라 3개월 단위로 구분하고, 영구보존은 최소 1년 이상 보존이 필요한 경우로 분류한다. 그림 8은 데이터의 사용빈도에 따른 분류이다. 실시간 데이터는 높은 사용빈도가 발생하나 연속성을 위한 데이터는 복제 발생시, 감사를 위한 데이터는 감사자료 필요시점 등 빈도 관점에서 분석한다. 성능은 실시간 처리를 위한 고성능과 감사용은 저성능으로도 충족되므로, 그림 9처럼 필요성능 분석을 수행한다. 위와 같은 분류 과정을 통해 각 시스템에 필요한 데이터의 용도와 빈도, 수명의 연관성을 그림 10과 같이 분류하였다. 데이터의 상관관계에 맞추어 서비스 유형별 필요한 스토리지의 상관관계를 분석하면 그림 11과 같다. 그림 12는 클라우드 스토리지 복합 배치모델이다. 각 서비스는 용도에 맞춰 3~4가지 유형의 다른 스토리지가 적합한 것으로 분석되었다. 3.5 머신러닝을 통한 스토리지 비용 예측예산은 연간 총TCO 예측과 예산소진 시기예측이 중요하다. 스토리지 비용은 시간에 따라 누적 증가하다가 이벤트 시기에 추세가 급변하는 특성이 있다. 이러한 비용예측은 선형회귀의 ARIMA 이용을 고려할 수 있으나, 이벤트에 따른 비선형 적특성과 다양한 변수조합을 이용한 장기예측은 순환신경망(RNN)이 더 효과적이다. RNN의 LSTM은 시계열 변동성에 대한 다양한 예측 연구가있다. M. H. Lee et al.의 바닥난방 제어를 위한 실내 온도예측[19], J. J. Jong, J. Y. KIM의 주가 예측[20], S. C. Park, Y. H. Kim의 서버 CPU 사용율 예측이다[21]. 본 연구는 이전 연구의 단층구조와 다르게 알고리즘 1과 같이 LSTM 다층구조를 사용하고 과적합과 학습안정화에 중점을 두었다. 필요 예산예측을 위한 데이터 구조는 그림 13과 같이 과거 1년간의 시뮬레이션 데이터 366개를 사용한다. 데이터는 전일과의 차분에 로그 변환 적용 후 전체를 8:2의 비율로 학습데이터와 시험데이터로 나누어 그림 14처럼 사용한다. 과거참조(look_back) 기간은 90, 180, 270일로 시험한 결과 그림 15처럼 90일에서 가장 안정적인 결과를 나타냈다. 에포크 진행에 따라훈련과 검증의 손실차이가 거의 없어 과적합이 없는 안정적인 상태로 확인된다. 시험에 사용한 최적의 하이퍼파라미터는 표 3과 같다. 모델을 4개층으로 구성하고, 과적합 방지를 위해 탈락(Dropout)과 L2정규화를 적용하였다. 데이터는 과거 1년간의 스토리지 증가 데이터를 사용하며, 옵티마이저, 활성함수, 배치크기 등은 여러 설정으로 시험한 최적의 값이다. 시험에 사용한 소스코드는 깃허브[22]에 게시되어 있다. 표(Table) 3. LSTM에 사용한 하이퍼파라미터 (Hyper-Parameters Used in LSTM)
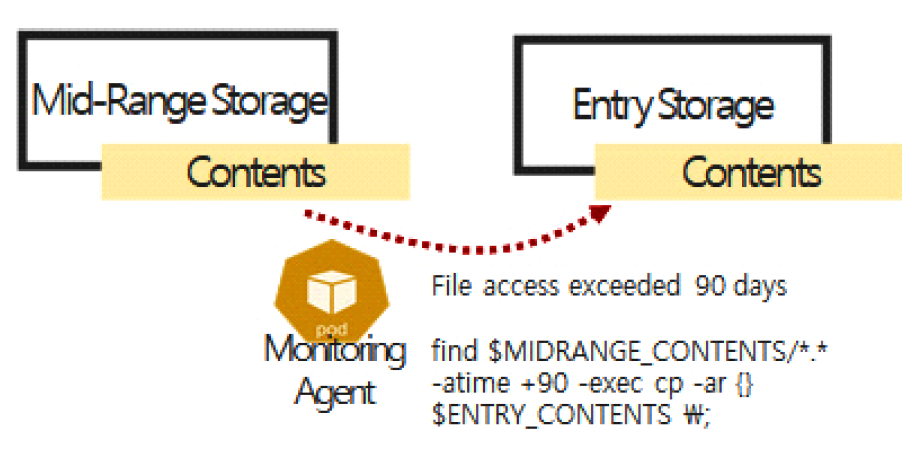
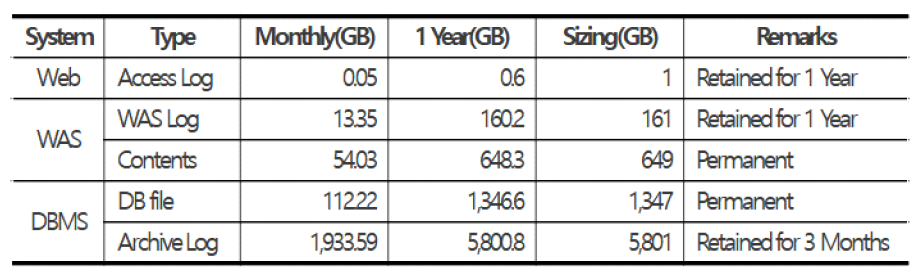
3.6 데이터 재배치서비스 데이터에서 빈도가 낮아도 삭제할 수 없는 데이터는 첨부파일 같은 콘텐츠 파일이다. 콘텐츠 파일은 용량은 크지만, 시간이 지날수록 빈도가 줄어든다. 접근 빈도가 낮아져 미참조 상태가 된 파일은 저비용의 스토리지로 재배치하면 저장비용을 더욱 최적화할 수 있다. 운영체제의 색인노드(Inode)에는 파일의 변경, 수정, 접근 시간정보가 저장되어 있다. 파일의 접근 90일 이상 참조 기록이 없는 파일을 장기 미참조 파일로 정의하고, 저비용 스토리지로 재배치하여 저장비용을 최적화한다. 그림 16은 재배치 에이전트의 역할을 나타낸다. 기존의 스토리지 재배치 연구들은 주로 멀티 클라우드 재배치나 용량 최적화에 초점을 맞추고 있어, 실시간 누적 데이터의 특성과 이벤트성 데이터 급증과 같은 복합적인 특성까지 통합적으로 고려하는 데는 한계가 있었다. 본 연구는 복합 스토리지 재배치 모델을 통해 데이터 수명, 사용빈도, 특성을 통합적으로 반영하고, 머신러닝 기반 예산 소모시기 예측으로 비선형적 비용 변동성까지 사전에 대응할 수 있는 실질적인 관리체계를 제안함으로써 차별성을 갖는다. Ⅳ. 구현 및 시험평가4.1 시험 개요본 연구의 성능시험은 웹서비스를 구성하는 3계층에서 계층별 자체생산 데이터의 특성을 활용한다. 중대형 규모의 기존 시스템 환경의 스토리지 데이터를 유형별로 분석한 결과는 그림 17과 같다. 서비스 데이터는 DB 파일과 콘텐츠 파일인 첨부파일이 큰 비율로 증가한다. 특히, 복구를 대비한 DB 아카이브 로그가 용량이 크지만, 다음번 로그로 대체되는 특성으로 일정한 용량을 유지하는 것이 확인되었다. 이런 용도와 증가 특성에 맞추어 복합 스토리지에 배치하고, 활용 빈도가 저하되는 시점에 재배치를 통해 핀옵스 최적화를 지원한다. 스토리지 서비스는 용량, 기간, 행위에 따라 비용이 발생한다. 표 4는 구글의 스토리지 서비스의 계층별 요금표이다. 계층에 따라 비용이 다르며 특히, 기간 미준수 패널티(Early Delete)가 있어 최소 저장기간 미준수 시에는 패널티 비용이 발생한다. 표(Table) 4. 구글 클라우드 스토리지 서비스 요금표 (Cost for Storage Service by Google)
단순한 스토리지 저장비용은 식(1)과 같이 저장된 용량과 작업비용의 연산으로 계산한다.
(1)[TeX:] $$$$ \begin{aligned} & C_{\text {current }}^k(t)=\left(t \cdot V_s^k \cdot C_s^k\right) \\ & C_{\text {total }}=\sum_{k \in\{S, N, C, A\}} C_{\text {current }}^k(t) \end{aligned} $$ - $C^{S, N, C, A}$ : Cost of Storage - $C_s \quad$ : Cost for File Access Action - $V_s \quad$ : Saved Volume - $t$ : Save Duration - $C_{\text {current }}^k$ : Currentused costby Storage - $C_{\text {total }}$ : Total cost$$TCO를 최소화하는 최적의 스토리지를 선정하기 위해 최소 저장기간 [TeX:] $$T_{\text {left }}$$를 식(2)와 같이 계산한다.
(2)[TeX:] $$$$ T_{l e f t}^k= \begin{cases}0, & t \bmod T_{\min }^k=0 \\ T_{\min }^k-\left(t \bmod T_{\min }^k\right), & \text { otherwise }\end{cases} $$ - $T_{\text {min }}^k \quad$ : Minimum Storaed Duration - $T_{\text {left }}^k \quad:$ Days - left for minimum period$$마이그레이션 비용은 현재의 저장비용과 잔여기간에 대한 비용으로 식(3)과 같이 산정한다.
(3)[TeX:] $$\begin{aligned} &C_{m i g}^k(t)=C_s^k+\left(T_{l e f t}^k \cdot V_s \cdot C_d^k\right)\\ &\text { - } C_{m i g}^k \quad \text { : Cost for Migration } \end{aligned}$$최적의 스토리지 비용은 마이그레이션 비용과 데이터의 읽기비용, 전송비용을 합산하여 식(4)와 같이 최소 비용이 소요되는 스토리지를 선정한다.
(4)[TeX:] $$\begin{aligned} & C_{\text {total }}^k=C_{\text {mig }}^k(t)+\left(f_{\text {read }} \cdot V_s \cdot C_r^k\right)+\left(V_s \cdot C_t^k\right) \\ & k^*=\underset{k}{\operatorname{argmin}} C_{\text {total }}^k \\ & \text { - } f_{\text {read }}: \text { ReadFrequency } \\ & \text { - } C_{r, t}: \text { Costfor Read, Transfer } \end{aligned}$$위의 과정을 알고리즘 2와 같이 나타낼 수 있다. 재배치는 보다 복잡한 고려가 필요하다. [TeX:] $$C_s^N$$의 저장 데이터의 데이터 미참조 기간이 90일 이상이면 재배치 대상이 되나, 저장비용과 전송비용, 기간 미준수 패널티를 포함한 비용이 [TeX:] $$C_s^C$$ 저장비용보다 이익일 때 재배치를 선택하는 식(5)와 같이 수행한다.
(5)[TeX:] $$\begin{aligned} & C_{\text {cost }}^N(t)=\max \left(T_{\min }^N, t\right) \cdot V_s \cdot C_s^N \\ & C_{\text {penalty }}^N(t)=\left(T_{\min }^N-t\right) \cdot V_s \cdot C_d^N,\left(\text { ift } \lt T_{\min }^N\right) \\ & C_{\text {total }}^N(t)=C_{\text {cost }}^N+C_{\text {penalty }}^N+\left(V_s \cdot C_t^{N \rightarrow C}\right) \\ & T_{\text {move }}=C_{\text {total }}^N \geq V_s \cdot C_s^C \end{aligned}$$재배치되면 서비스에 새로운 스토리지의 경로로 업데이트를 요청하여 서비스 품질을 유지한다.
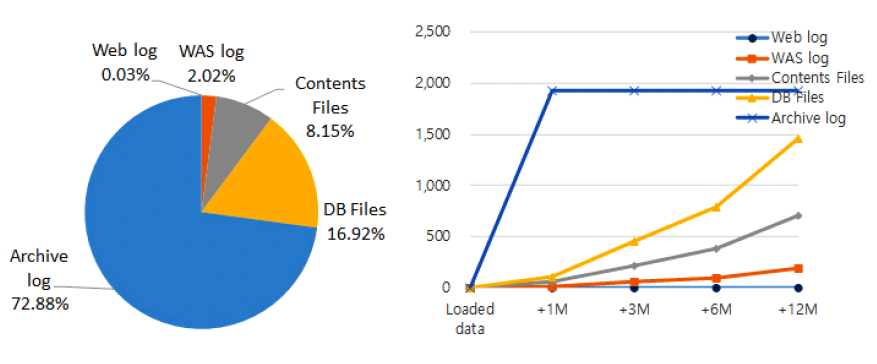
(6)[TeX:] $$Service Path $=$ FILE $_{\text {path }}^C$ - Service Path : Service acces s path - $F I L E_{\text {path }}^C$ : Updated file location after relocation$$4.2 성능비교분류에 사용한 중대형 기존 시스템의 스토리지 저장 데이터 현황은 그림 18과 같다. 여기에 매일의 증분과 보존기간 특성을 적용하였다. 현황 데이터를 바탕으로 데이터 증가를 적용한 전환 및 소요비용 예측은 표 5와 같다. 단일모델 대비 복합모델의 1년 후 사용비용은 약 56% 감소될 것으로 예측된다. 장기 미참조 재배치 에이전트를 적용하면 3개월부터 큰 차이로 감소하여 1년 후약 71.1%의 감소가 발생할 것이다. 표(Table) 5. 데이터 적재부터 1년간의 비용 비교표 (Cost Comparison Table)
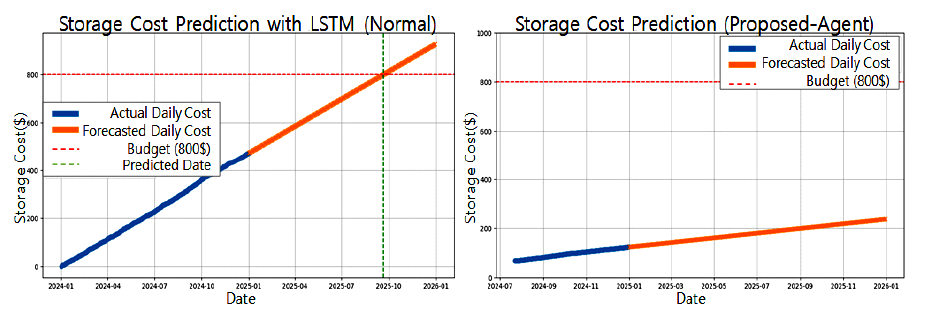
LSTM의 비용예측은 단일모델과 복합모델을 대상으로 향후 1년간의 비용 예측을 그림 19처럼 수행하였다. 동일 저장용량에 대하여 좌측의 단일모델보다 우측 복합모델이 비용 효과적임을 알 수 있다. 머신러닝 결과평가는 표 6과 같다. 평균절대오차 (MAE)와 평균제곱근오차(RMSE)의 분포가 일정하고, 평균절대비율오차(MAPE) 약 18%로 활용성이 있다고 평가할 수 있다. 표(Table) 6. LSTM을 이용한 미래 비용예측 결과 (Prediction Results using LSTM)
성능비교를 통해 제안기법이 클라우드에서 스토리지를 운영할 때 비용 효과적이며, 서비스 생명주기가 길어질수록 더 뚜렷한 비용절감 효과가 있다. 또한, 머신러닝 기술과 조합하여 이벤트성 비선형적인 변화를 포함한 비용예측이 가능하고, 예산초과시점을 사전에 확인하여 재배치하는 등 선조치도 가능하므로 관리 및 운영측면의 활용도가 높다. Ⅴ. 결 론본 연구는 클라우드 네이티브 환경에서 핀옵스를 달성하기 위한 핵심 요소 중 하나인 스토리지 TCO 최적화에 관한 것이다. 스토리지는 초기 적재 이후 지속 증가하는 자원으로, 배치 단계에서 장기적 관점의 데이터 배치모델 최적화 없이 핀옵스를 구현하는 데에는 한계가 있다. 기존의 장기 보존비용 절감 연구와 다르게, 본 연구는 서비스 운영 데이터의 스토리지 계층을 활용한 실시간성 최적화에 초점을 맞추고 있다. 중대형 규모의 기존 시스템 분석을 통해 데이터 특성을 파악하고, 이를 바탕으로 컨테이너 서비스 유형별로 최적의 계층 스토리지를 사용하는 복합모델을 개발하였다. 제안모델을 통해 기존 중대형 데이터를 클라우드로 전환 후 1년간 최소 50% 이상의 비용 절감이 가능하고, 장기 미참조 데이터의 재배치를 통해 더 효과적인 비용 최적화를 달성할 수 있음을 증명하였다. 또한, 단순 사용비용이 아닌 예산의 도달시점을 예측하여 예산 수립과 재배치 계획을 지원하는 머신러닝 적용방안도 연구하였다. 본 연구는 클라우드 비용 중 누적 증가하는 특성을 갖는 스토리지 데이터로 인한 비용을 절감하고 비선형적인 특징변화를 반영한 비용예측으로, 클라우드 환경에서 핀옵스를 효과적으로 지원하는데 기여할 것으로 기대된다. 특히, 본 연구는 스토리지의 단순한 비용 절감에 그치는 것이 아니라, 실시간 데이터 누적 특성, 저장 계층별 비용구조, 이벤트성 증분 패턴을 통합하여 복합적인 최적화 및 예측 체계를 제시하였다. 이를 통해 기존 연구들과 차별화된 실질적인 클라우드 핀옵스 지원 모델을 구축할 수 있음을 입증하였다. 하지만, 실험은 단일 시나리오를 기반으로 진행되었기 때문에 다양한 산업군이나 서비스 유형을 대상으로하는 일반화에는 한계가 있다. 비용평가 또한, Google 클라우드의 요금체계를 기반으로 하여 평가하여, 다른 CSP의 서비스 체계에 따른 요금차이 및 정책이 상이할 수 있어 적용시 주의가 필요하며 최적화 효과에서도 차이가 발생할 수 있다. 향후 연구에서는 데이터의 증가 특성을 중심으로 미디어 서비스, 전자상거래, 엣지 서비스 등 다양한 데이터 증분특성을 대상으로 복합 배치모델의 적용성과 한계성을 검증할 계획이다. 또한, 여러 CSP의 서비스 체계의 요금차이와 다른 예측모델(ARIMA, Prophet, Transformer 등)의 성능 차이에 대한 후속 분석도 수행할 예정이다. 아울러, 데이터 재배치에 따른 소스파일의 경로 자동변경, 중장기 저장파일의 운영모델 등에 대한 추가 연구도 필요하다. BiographyBiographyReferences
|
StatisticsCite this articleIEEE StyleS. Park and Y. Kim, "Design of a Storage Service Operation Model for Cloud Service Cost Reduction," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1568-1577, 2025. DOI: 10.7840/kics.2025.50.10.1568.
ACM Style Sun-chul Park and Young-han Kim. 2025. Design of a Storage Service Operation Model for Cloud Service Cost Reduction. The Journal of Korean Institute of Communications and Information Sciences, 50, 10, (2025), 1568-1577. DOI: 10.7840/kics.2025.50.10.1568.
KICS Style Sun-chul Park and Young-han Kim, "Design of a Storage Service Operation Model for Cloud Service Cost Reduction," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1568-1577, 10. 2025. (https://doi.org/10.7840/kics.2025.50.10.1568)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||