IndexFiguresTables |
Jungbin Yim♦ , Donghyun Kim* , Inmo Ban* and Namyoon Lee°Review on High Resolution Wide Swath SAR System Using Frequency ScanningAbstract: A key research topic in spaceborne synthetic aperture radar (SAR) systems is the development of high-resolution wide-swath (HRWS) imaging techniques that overcome the fundamental trade-off between image resolution and swath width. In general, achieving high resolution in SAR systems requires a high pulse repetition frequency (PRF), whereas wide-swath observation necessitates a lower PRF. To address this inherent limitation, various SAR techniques have been proposed. Among them, representative approaches for HRWS imaging include scanning on receive (SCORE) and frequency scanning (F-scan). This paper provides a tutorial overview of the valid PRF range for SAR image formation and illustrates the trade-off between resolution and swath width. Furthermore, it introduces the frequency scanning technique as a promising solution to this trade-off and demonstrates its effectiveness through simulation results. Keywords: high resolution wide swath SAR , beam squint , frequency scanning 임정빈♦, 김동현*, 반인모*, 이남윤°주파수 스캐닝을 이용한 고해상도 광역관측 SAR 시스템 리뷰요 약: 위성 기반 synthetic aperture radar (SAR)의 고해상도 광역관측 기술은 SAR의 해상도와 관측폭 간의 상충 관계를 극복하기 위한 핵심 연구 주제이다. 일반적으로 SAR 시스템에서 고해상도를 구현하기 위해서는 pulse repetition frequency (PRF)를 높여야 하는 반면, 광역관측을 구현하기 위해서는 PRF를 낮춰야한다. 이러한 한계점을 극복하기 위해 다양한 SAR 기술이 제안되어왔으며, 대표적인 고해상도 광역 관측기술로는 수신채널 스캔(scan-on-receive, SCORE)과 주파수 스캐닝(frequency scanning, F-scan)이있다. 본논문은튜토리얼로써 SAR 이미지를 생성하기 위한 PRF 범위를 설명하고 고해상도와 광역관측이 서로 상충관계에 있음을 보인다. 또한, 이를 극복하는 기술로써 빔 스퀸트를 이용하는 주파수 스캐닝 기술에 대해 소개하고 이에 대한 모의 실험 결과를 통해 이 기술의 효용성을 입증한다. 키워드: 고해상도 광역관측 SAR, 빔 스퀸트, 주파수 스캐닝 Ⅰ. 서 론Synthetic aperture radar (SAR)는 위성과 항공기와 같은 움직이는 플랫폼에 탑재되어 지형을 관측하고 분석할 수 있는 기술로 1951년에 Carl Wiley에 의해 개념이 도입되면서 기존의 side looking airborne radar (SLAR)보다 훨씬 높은 해상도로 이미지를 형성할 수 있게 되어 지금까지도 많은 관심을 받고 있다[1,2]. SAR는 전자기파를 사용하기 때문에 어두운 밤이나 악천후인 환경의 영향을 받지 않고 장애물과의 거리를 정확히 추정할 수 있어 어떠한 환경에서도 높은 해상도의 이미지를 형성할 수 있다. 이러한 고해상도의 성능은 안테나가 탑재된 플랫폼이 이동하며 신호를 송수신하고 이 수신된 신호들을 코히어런트 결합함으로써 실제 안테나의 개구면보다 더 긴 가상의 안테나 개구면을 가진 효과를 통해 얻을 수 있다. 날씨 조건에 무관하며 넓은 영역의 이미지를 고해상도로 형성할 수 있는 이러한 SAR 시스템의 이미징 능력 덕분에 1950년대부터 많은 관심을 받아왔으며 많은 문헌들에서 상세히 정리된 SAR 시스템의 개념 및 원리를 찾아볼 수 있다[3-12]. 기존의 이미징 레이더 시스템인 SLAR는 높은 해상도를 얻기 위해서 안테나의 aperture size가 그만큼 커질 수밖에 없고 그러한 큰 aperture size의 안테나를 플랫폼에 탑재하기 어려웠다. 예를 들어, X 밴드를 사용하는 SLAR 시스템이 5 km 떨어진 영역을 이미징할 때, 1.5 m의 azimuth 방향으로의 해상도를 얻기 위해서는 100 m 크기의 안테나가 탑재되어야만한다. 하지만, SAR 시스템은 관측하고자 하는 영역의 거리와 상관없이 azimuth 방향으로의 해상도가 결정되며 앞의 SLAR 시스템의 예시에서와 동일한 상황에서 같은 azimuth 방향으로의 해상도를 달성하기 위해서 SAR 시스템은 3m의 안테나 길이로 충분하다. 또한, 관측 거리가 멀어질수록 SLAR는 azimuth 방향으로의 해상도가 안좋아지지만 SAR는 관측 거리와 해상도가 서로 무관하여 항공기와 같은 비행체뿐만 아니라 더 고도가 높은 위성을 이용한 SAR 시스템을 통해서도 고해상도의 이미지 생성이 가능하다. 이러한 이유로 인해 비행체 기반의 SAR 시스템을 시작으로 1978년에는 NASA에 의해 최초로 위성 기반의 SAR 시스템이 구현되었다. Seasat을 필두로, 계속해서 위성 탑재 기반의 SAR는 많은 관심을 받고 연구되어 2000년대에는 TerraSAR-X와 TanDEM-X와 같은 위성 기반의 SAR 시스템이 개발되었으며 최근까지도 더 높은 해상도와 더 넓은 영역을 관측할 수 있는 SAR 시스템을 구현하기 위해 연구되고있다. 하지만, SAR 시스템은 일정 이상의 높은 해상도와 넓은 관측 영역을 동시에 달성할 수 없는 근본적인 문제를 지니고 있다. SAR 시스템에서 azimuth와 range 방향 모두에 대해서 ambiguity 없는 선명한 이미지를 형성하기기 위해서는 pulse repetition interval (PRI) 즉, pulse repetition frequency (PRF)를 잘 조절해야만 한다. PRF를 잘 조절해야하는 이유는 azimuth 방향으로의 해상도에 대해서는 하한을 그리고 관측 영역에 대해서는 상한을 가지고 있기 때문이다[13]. 하지만, 점차 더욱 높은 azimuth 방향으로의 해상도와 넓은 관측 영역을 요구하는 현대의 SAR 시스템은 이 두 조건을 동시에 만족하는 PRF를 선택할 수 없게 된다. 이러한 SAR 시스템의 주요 요구 조건인 azimuth 방향으로의 높은 해상도와 넓은 관측 영역을 달성하기 위해서 기존의 stripmap mode 이외에도 scan-SAR 모드와 spotlight 모드와 같은 여러 동작 모드들이 개발되었다[14]-[16]. 하지만, 이 동작 모드들은 azimuth 방향으로의 해상도와 관측 영역 중 어느 한 요구조건을 희생하여 다른 요구 조건을 충족시키는 방법이다. 따라서, 이러한 동작 모드들로 두 요구 조건 중 어느 한 쪽을 만족시키는 것은 가능하지만 동시에 두 조건을 만족시키는 것은 여전히 근본적으로 불가능하다. 하지만, 이러한 문제를 해결하기 위해서 최근에 많은 연구가 이루어졌으며 이를 해결하기 위한 대표적인 방법으로는 디지털 빔포밍 기술을 이용한 scan-on-receive (SCORE)와 주파수 스캐닝 (frequency scanning, F-scan) 기술이 있다. 특히, SCORE는 azimuth 방향으로는 multiple aperture processing scheme (MAPS)라고도 불리며 이 두 기술은 SAR 시스템이 근본적으로 내재하고 있는 문제를 해결할 수 있다[17]-[26]. 먼저, MAPS는 azimuth 방향으로 다수의 sub-aperture 구조로 SAR 시스템을 구성하여 한번의 PRI동안 여러 신호를 동시에 수신할 수 있게 만든다. 따라서, 관측 영역에 해당하는 PRF의 조건을 변화시키지 않고 azimuth 방향으로의 실질적인 PRF가 증가한다. 즉, 한번의 송신 신호를 통해 여러 신호를 동시에 수신하여 azimuth 방향으로의 샘플을 늘리는 것이다. 이를 통해, PRF의 상한과 하한 조건을 검증할 때 각 조건에 대해서 실질적으로 이용되는 PRF가 달라져 sub-aperture 개수를 잘 조절함으로써 두 조건을 동시에 만족시킬 수 있게 된다. 반면에, range 방향으로의 SCORE와 주파수 스캐닝 기술은 PRF의 상한을 올릴 수 있는 기술이다. 먼저, SCORE는 MAPS와 마찬가지로 여러 개여 sub-aperture 구조로 SAR 시스템을 구현하여 range 방향으로 여러 sub-swath를 동시에 관측한다. SAR 시스템의 PRF 상한은 관측하고자하는 영역의 가장 가까운 부분과 가장 먼 부분을 신호가 왕복하는 시간의 차인 echo duration에 반비례하기 때문에 이 echo duration을 줄일수록 PRF의 상한이 증가하게 된다. 기존의 SAR 시스템은 관측 영역이 넓어질수록 이 echo duration이 커지게 되고 그에 따라 PRF의 상한이 감소하여 그만큼 azimuth 방향으로의 해상도를 줄일 수밖에 없다. 하지만, SCORE는 이러한 넓은 swath를 공간상으로 분할하여 각 sub-swath에 대해서 sub-aperture들이 커버하는 방식으로 공간상으로 분할된만큼 줄어든 관측 영역으로 인해 echo duration을 감소시켜 PRF의 상한을 증가시킬 수 있다. 또한, 관측 영역이 너무 넓을 경우에 플랫폼에 탑재된 안테나의 빔 폭이 관측 영역을 커버하기에 너무 좁을 때 발생할 수 있는 낮은 signal-to-noise ratio (SNR)로 인한 이미징 성능 저하 문제도 해결할 수 있다. 빔 폭이 좁으면 실제 관측하고자 하는 영역들 중 일부분은 매우 적은 이득으로 빔이 송수신되어 상당히 낮은 SNR로 이미징 성능이 저하된다. 하지만, SCORE는 기존의 SAR 시스템보다 더 좁고 강한 이득의 빔을 여러 개 형성하여 sub-swath들을 커버함으로써 빔 폭에 따른 이미징 성능 문제와 PRF의 상한을 모두 개선할 수 있는 방법이다. 이러한 장점들에도 불구하고, SCORE 기술을 구현하기 위해서는 여러 sub-aperture로 SAR 시스템을 구성해야하기 때문에 그만큼 더 많은 RF-chain이 요구되고 따라서 하드웨어가 굉장히 복잡해진다. 따라서, 최근에는 이 SCORE 기술의 장점들은 모두 그대로 이용할 수 있으면서 하드웨어의 부담을 많이 줄일 수 있는 주파수 스캐닝 기술이 많은 관심을 받고 연구되고 있다. 따라서, 본 논문은 이러한 주파수 스캐닝 기술을 이용한 SAR 시스템 튜토리얼 리뷰 논문으로써 먼저 PRF의 상한과 하한을 유도하여 고해상도와 광역 관측을 왜 동시에 달성할 수 없는지를 설명하고 이에 대한 해결 방안인 주파수 스캐닝 기술을 소개한다. 또한, 주파수 스캐닝 기술이 SCORE에 비해 가지는 장점과 함께 실제 구현을 위해 요구되는 후처리 과정을 소개하고 시뮬레이션을 통해 주파수 스캐닝에서 후처리 유무에 따른 결과를 기반으로 주파수 스캐닝 기술 기반의 SAR 시스템의 성능을 입증한다. Ⅱ. PRF의 선택 가능 범위SAR 시스템을 통한 이미지 획득은 range와 azimuth 방향으로의 compression을 통해 가능하지만 ambiguity 없이 선명한 이미지 획득을 위해서는 추가적으로 고려해야할 사항이 존재한다. SAR 시스템은 비행체가 움직이면서 신호를 반복적으로 송수신하고 이를 통해 모은 raw data를 코히어런트 결합하여 이미지를 생성하기 때문에 신호의 송수신을 반복하는 주기인 PRI가 이미징 성능의 중요한 요소로 작용한다. PRI를 적절하게 설정하지 않으면 range 방향 혹은 azimuth 방향으로 ambiguity가 발생하게 되기 때문에 시스템이 요구하는 요구 조건에 맞는 적절한 PRI를 선택하여 운용하는 것이 굉장히 중요하며 이에 대한 PRI 선택 가능 범위를 아는 것이 SAR 시스템 구현에 있어서 필수적으로 요구된다. 즉, PRI의 역수로 정의되는 PRF를 적절하게 설정하는 것이 중요하고 이를 통해 먼저 azimuth 방향으로의 해상도와 관측 영역을 만족할 수 있는 PRF의 범위를 이 섹션을 통해 살펴본다. PRF의 상한은 SAR의 관측 영역과 관련이 있는 파라미터로써 비행체에서 송신된 신호가 비행체로부터 관측하고자 하는 영역의 가장 먼 부분과 가장 가까운 부분을 왕복하면서 걸리는 시간 차이에 의해 결정된다. 따라서, 이 시간 차이는 비행체로부터 관측하고자 하는 영역의 가장 먼 부분과 가장 가까운 부분까지의 거리를 2배하여 빛의 속도로 나눈 값의 차이로 계산되며 echo duration으로 정의된다. 이 echo duration이 PRI를 넘지않아야 하며 만약 그렇지 않을 경우 특정 slow-time η에서의 송신 신호에 대한 대상물을 맞고 반사되어 들어오는 신호가 다음 신호가 송신되는 η + PRI 이후에 수신되어 range 방향으로의 ambiguity가 발생한다. 따라서, 먼저 PRI의 하한이 다음과 같은 식으로 정해진다.
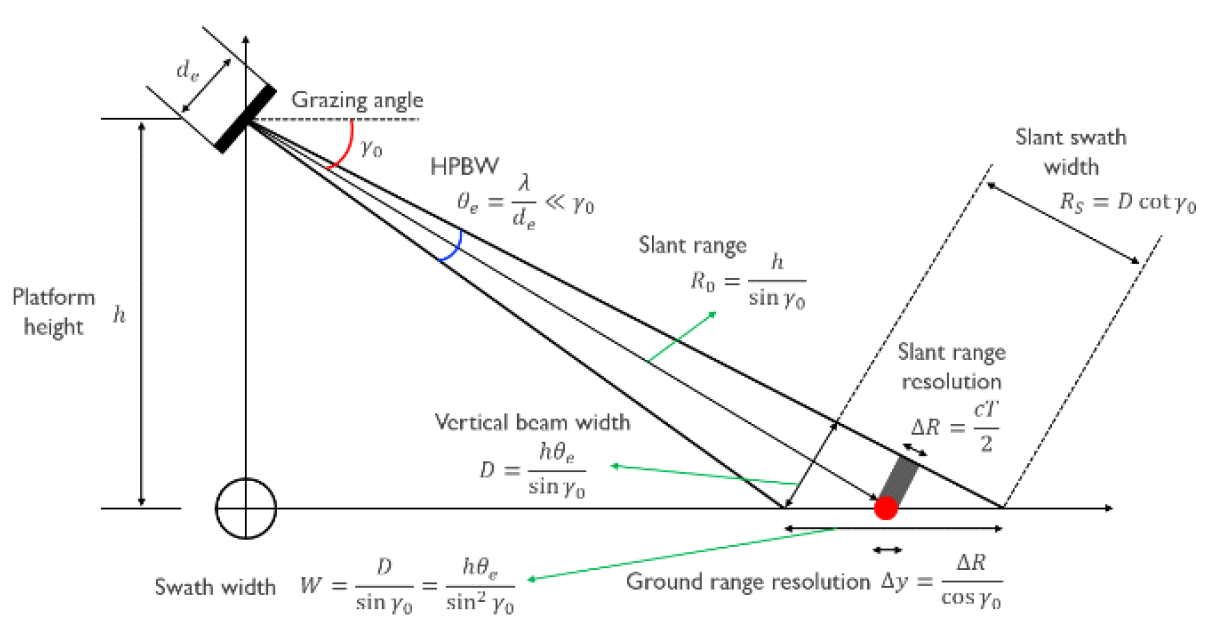
이때, [TeX:] $$R_S$$는 그림 1에서와 같이 비행체로부터 관측 영역의 가장 먼 부분과 가장 가까운 부분의 거리 차이고 c는 빛의 속도이다. 결론적으로, 위 식의 역수를 구함으로써 PRF의 상한은 다음과 같이 결정된다.
위 식을 통해, 넓은 관측 영역의 이미지를 얻기 위해서는 그만큼 [TeX:] $$R_S$$가 커지기 때문에 낮은 PRF가 요구됨을 알 수 있다. 다음으로, PRF의 하한은 azimuth 방향으로의 해상도와 관련이 있다. Azimuth 방향으로의 data 획득 즉, sampling은 Nyquist sampling 이론에 의해 azimuth 방향으로 발생하는 Doppler bandwidth [TeX:] $$B_D$$보다 sampling rate이 커야만 한다. 이는 aliasing이 발생하지 않게하기 위함이며 이러한 공간상의 aliasing을 azimuth ambiguity라고 정의한다. 이 azimuth 방향으로의 sampling rate이 결국 PRF이기 때문에 다음과 같은 PRF의 하한이 정해진다.
이때, Doppler bandwidth [TeX:] $$B_D$$는 대상물에 대한 echo 신호의 위상을 이용하여 구할 수 있다. Slow-time η에서 대상물에 대한 echo 신호의 위상 [TeX:] $$\phi(\eta)$$은 다음과 같이 계산된다.
(4)[TeX:] $$\phi(\eta)=\frac{4 \pi R(\eta)}{\lambda} \approx \frac{4 \pi R_0}{\lambda}+\frac{2 \pi v_p^2}{R_0 \lambda} \eta^2 .$$이때, [TeX:] $$\mathrm{R}(\eta)$$는 slow-time η에서의 비행체와 대상물까지의 거리이며 [TeX:] $$R_0$$는 비행체가 대상물과 가장 가까워졌을 때의 비행체와 대상물 사이의 거리이다. 또한, λ와 [TeX:] $$v_p$$는 신호의 파장과 비행체의 속도이다. 따라서, η에서의 즉각적인 위상의 변화는 다음과 같이 구할 수 있다.
(5)[TeX:] $$\sigma(\eta)=\frac{1}{2 \pi} \cdot \frac{\partial \phi(\eta)}{\partial \eta}=\frac{2 v_p^2}{R_0 \lambda} \eta .$$이때, 비행체가 대상물에 대해 illumination time 동안 신호를 송수신하기 때문에 이 시간동안의 위상 변화가 Doppler bandwidth가 된다. SAR의 합성 개구의 길이를 L이라고 했을 때, L은 비행체가 대상물과 가장 가까워졌을 때의 비행체와 대상물사이의 거리인 [TeX:] $$R_0$$와 안테나가 형성하는 azimuth 방향의 half power beamwidth (HPBW)인 [TeX:] $$\theta_a$$의 곱으로 계산되고 이를 비행체의 속력으로 나눈 것이 illumination time 이므로 illumination time [TeX:] $$\eta_{\mathrm{tot}}$$는 다음과 같이 계산된다.
위 식에서, [TeX:] $$d_a$$는 azimuth 방향으로의 안테나 길이이며 azimuth 방향의 HPBW가 다음과 같이 [TeX:] $$d_a$$에 대한 식으로 계산되는 것을 이용한 것이다.
결론적으로, 이 illumination time을 위상 변화 [TeX:] $$\sigma(\eta)$$에 대입하여 Doppler bandwidth를 다음과 같이 구할 수 있다.
따라서, 식 (3)에서의 PRF에 대한 하한을 구체적으로 다음과 같이 구할 수 있다.
이때, Doppler bandwidth의 역수를 통해 azimuth 방향으로의 time resolution을 구할 수 있다. 또한, 이 time resolution에 비행체의 속력을 곱해 azimuth resolution을 구할 수 있으며 이를 통해 PRF의 하한을 azimuth resolution에 대한 식으로 바꿀 수 있다. 먼저 azimuth resolution [TeX:] $$\delta_a$$은 다음과 같이 계산된다.
위 식을 통해, 우리는 SAR의 azimuth 방향으로의 해상도가 대상물까지의 거리와 무관하며 azimuth 방향으로의 안테나 길이가 작을수록 증가한다는 것을 알 수 있다. 이러한 경향성은 직관에 반대되는 것처럼 보이지만 SAR의 해상도는 합성 개구의 길이에 의존하기 때문에 azimuth 방향으로의 HPBW가 넓을수록 좋은 해상도를 가진다. 따라서, 식 (7)에서와 같이 azimuth 방향으로의 넓은 HPBW를 얻기 위해서는 좁은 안테나 길이가 요구된다. 결론적으로 SAR는 azimuth 방향으로의 안테나 길이의 절반에 의해 azimuth 방향으로의 해상도가 결정된다. 이러한 azimuth 방향으로의 해상도를 PRF의 하한 조건으로 만들기 위해 식 (9)를 조금 변형하여 다음과 같이 다시 쓸 수 있다.
따라서, 위 식을 통해 [TeX:] $$R_S$$에 의한 PRF 조건과는 반대로 azimuth 방향의 해상도를 높이기 위해서는 높은 PRF가 요구됨을 알 수 있다. 결과적으로, 식 (2)와 (11)에 해당하는 PRF의 상한과 하한을 동시에 고려하면 다음과 같은 부등식이 성립한다.
위 식에서, PRF는 azimuth 방향으로의 해상도가 증가할수록 높은 PRF가 요구되고 관측 영역인 swath width가 넓어질수록 [TeX:] $$R_s$$가 증가하므로 낮은 PRF가 요구된다. 이러한 상충되는 PRF의 요구조건은 어느 한쪽의 요구 조건을 만족하기 위해서는 다른 한쪽의 요구 조건이 완화되어야함을 의미한다. 따라서, 운용되는 SAR 시스템의 PRF를 선택함에 있어서 azimuth 방향으로의 해상도와 관측할 수 있는 영역의 한계치가 정해지고 이러한 한계치를 넘어갈 경우에는 ambiguity가 발생하기 때문에 이미지 처리 성능이 매우 저하된다. 그러므로, 양쪽 모두 높은 성능을 요구하는 현대의 SAR 시스템은 어떠한 PRF를 선택하더라도 적어도 어느 한쪽은 ambiguity가 발생할 수밖에 없는 내재적인 한계점을 지니고 있다. 이러한 한계점을 극복하기 위한 기술로 이용할 수 있는 MAPS는 한번의 신호 송신으로 azimuth 방향으로의 여러 개의 sub-aperture를 통해 다수의 echo 신호를 수신함으로써 식 (2)에서의 PRF를 기준으로 식 (11)에서의 azimuth 방향으로의 해상도에 대해서는 만약 N개의 sub-aperture로 구성되어있다고 가정한다면 effective PRF가 N․PRF로 증가되도록 만드는 기술이다. 따라서, 식 (2)에 대해서는 PRF로 조건의 상한을 만족하면 되고 식 (11)에 대해서는N․PRF로 하한을 만족하게 할 수 있다. 결과적으로, 원하는 관측 영역이 정해지면 그에 따라 PRF의 상한이 정해지게되고 이 상한 내에서의 PRF로 azimuth 방향으로의 해상도를 만족시킬 수 없다면N을 통해 effective PRF를 늘려 해상도를 만족할 수 있게 된다. PRF의 하한에 해당하는 effective PRF를 늘려 식 (12)의 PRF 조건을 만족시키는 기술인 MAPS와 달리 range 방향으로의 SCORE와 주파수 스캐닝 기술은 식 (12)에서 상한에 포함된 [TeX:] $$R_s$$를 줄일 수 있는 기술이다. Azimuth 방향으로 여러 sub-aperture로 구성됐던 MAPS와 달리 SCORE는 elevation 방향으로 여러 sub-aperture 구조로 SAR 시스템이 구성된다. 이러한 구조를 통해, MAPS와 유사하게 한번의 신호 송신으로 인해 동시에 여러 수신 신호를 얻을 수 있게 된다. 따라서, 이러한 구조를 이용하여 한번의 넓은 송신 빔을 이용하여 신호를 송신하고 송신 빔이 커버하는 관측 영역을 sub-aperture의 개수로 분할하여 각 sub-aperture는 그 sub-aperture에 해당하는 sub-swath의 데이터들을 수신하여 처리한다. 따라서, sub-swath로 분할된 각 sub-aperture의 관측 영역은 그만큼 range 방향으로의 길이가 줄어들고 그에 따라 [TeX:] $$R_s$$가 감소하게 된다. 이에 따라, echo duration이 감소하여 식 (2)에서의 PRF의 상한이 증가하게 된다. 결과적으로, 고해상도와 광역 관측을 만족하기 위해서 요구되는 식 (12)에서의 PRF의 하한과 상한의 가능한 범위가 생기게 만들 수 있게 된다. 또한, SCORE는 디지털 빔포밍을 통해 각 sub-swath에 대해서 기존의 SAR 시스템보다 echo 신호를 수신할 때 훨씬 이득이 크고 좁은 빔을 형성하여 수신하기 때문에 PRF 조건을 만족시킬 수 있게 상한을 증가시키는 것 외에도 SNR 향상을 통해 더 좋은 이미징 성능 또한 얻을 수 있게 된다. 하지만, 그만큼 기존의 SAR 시스템보다 많은 하드웨어가 요구되고 그에 따라 시스템도 복잡해진다. 따라서, SCORE의 이 복잡한 하드웨어 구조 때문에 고해상도 광역관측을 위해 처리되야하는 데이터가 굉장히 많은 현대 SAR 시스템은 주파수 스캐닝 기술을 이용하는 것을 선호하고 있다. Ⅲ. 주파수 스캐닝을 이용한 고해상도 광역관측 SAR 시스템주파수 스캐닝 기술은 넓은 대역폭을 이용함으로써 발생하는 빔 스퀸트 현상을 이용한다. SCORE와 식 (12)에서의 PRF 상한을 높이는 근본적인 원리는 똑같지만 여러 개의 sub-aperture를 통해 이미징되던 영역을 주파수 스캐닝은 광대역의 송신 chirp 신호가 자연스럽게 발생시키는 빔 스퀸트를 이용하여 스캔하는 방식으로 관측 영역을 이미징한다[27]. 따라서, SCORE와 달리 안테나 구조를 여러 sub-aperture 구조로 구성할 필요없이 기존의 SAR 시스템과 동일하게 구현할 수 있다. 이 외에도, SCORE는 신호를 수신할 때에는 이득이 크고 좁은 빔을 사용하지만 신호를 송신할 때에는 넓은 관측 영역을 모두 커버하기 위해 aperture size가 비교적 작은 안테나를 이용하거나 테이퍼링을 통해 송신 빔 폭을 넓힌다. 따라서, 송신 빔 이득은 수신 빔에 비해 작을 수밖에 없다. 하지만, 주파수 스캐닝 기술은 송수신 빔 모두 SCORE의 수신 빔과 같이 매우 이득이 크고 좁은 빔을 사용하기 때문에 SCORE보다도 높은 SNR을 통해 좋은 성능의 이미지를 얻을 수 있다. 또 하나의 추가적인 주파수 스캐닝의 장점으로는 SCORE보다 적은 수의 데이터를 수신하고 처리하여 하드웨어의 부담을 줄일 수 있다는 것이다. 고해상도 광역관측 SAR 시스템은 기존의 SAR 시스템보다 굉장히 많은 데이터를 저장하고 처리하여야하기 때문에 onboard 하드웨어의 부담이 매우 크다. SCORE는 여러 개의 sub-aperture로 구성되기 때문에 이러한 하드웨어 부담이 배로 증가하게 된다. 반면에, 주파수 스캐닝 기술은 단일 aperture 구조로 하드웨어 구조도 단순할 뿐만 아니라 신호를 수신할 때 송신한 chirp 신호 전부를 수신하는 것이 아니라 일부만을 수신한다. 따라서, 추후에 이를 복원하는 후처리 과정이 필요하긴 하지만 훨씬 줄어든 데이터로 인해 onboard의 부담이 매우 줄게 된다. 따라서, 실제 고해상도 광역관측 SAR 시스템을 구현할 때에도 하드웨어적인 측면에서의 한계도 함께 해결할 수 있다. 주파수 스캐닝 기술은 넓은 대역폭의 송신 chirp 신호를 이용하여 바뀌는 주파수에 따라 자연스럽게 발생하는 빔 스퀸트를 이용하여 방사 각도가 달라지는 pencil beam을 이용한다. 이때, 만약 관측하고자 하는 영역이 너무 넓으면 매우 큰 대역폭이 요구된다. 따라서, 계속해서 넓어지는 관측 영역의 요구 조건 때문에 현대의 고해상도 광역관측 SAR 시스템은 관측 영역을 모두 커버할만큼 넓은 대역폭을 사용하지 못할 수도 있다. 이를 해결하기 위한 것이 true time delay (TTD)이다. TTD는 기존의 phase shifter (PS)로 빔을 조향하던 것에서 추가적으로 위상을 조절할 수 있다. 만약 신호가 q의 zenith 각도로 배열 안테나로 들어온다면, 배열 안테나의 인접한 안테나들의 위상 차이는 다음과 같다.
이때, d는 인접한 두 안테나 사이의 거리이다. 빔은 PS를 통해 이 위상 차이를 보정함으로써 θ의 방향으로 빔을 조향할 수 있게 된다. 이때, 식 (13)에서 파장이 대역폭이 좁을때에는 중심 주파수에 해당하는 파장으로 근사하여 빔 스퀸트가 발생하지 않지만 대역폭이 넓을 때에는 대역폭 양끝의 주파수는 중심 주파수와 차이가 커서 이 차이를 무시할 수 없게 된다. 따라서, chirp 신호를 송신하면서 시간에 따라 바뀌는 파장이 PS에 의해 똑같이 위상을 보정하더라도 그만큼 조향하는 각도 θ가 바뀌게 된다. 이것이 빔 스퀸트 현상이다. 만약 사용하는 chirp 신호의 대역폭을 [TeX:] $$B_{c h}$$라고 했을 때, 대역폭에 의해서 발생하는 빔 스퀸트로 인해 달라지는 조향 각도 차이는 다음과 같이 계산된다.
(14)[TeX:] $$\begin{aligned} \Delta \theta= & \sin ^{-1}\left(\frac{f_c}{f_c-\frac{B_{c h}}{2}} \cdot \sin \theta\right) \\ & -\sin ^{-1}\left(\frac{f_c}{f_c+\frac{B_{c h}}{2}} \cdot \sin \theta\right) . \end{aligned}$$만약, 빔 스퀸트만으로 관측하고자하는 영역 전체를 커버할 수 있으면 사용되는 대역폭이 충분한 것이지만 그렇지 않다면 더 넓은 대역폭을 사용해야만한다. 하지만 대역폭을 넓히는 것은 한계가 있기 때문에 무한하게 관측 영역을 넓힐 수 없다. 따라서, TTD를 이용함으로써 이를 해결한다. 배열 안테나에 PS뿐만 아니라 TTD까지 함께 결합한다면 추가적으로 위상을 다음과 같이 조절할 수 있게 된다.
위 식에서, [TeX:] $$\Delta \tau$$는 TTD를 통해 보상되는 위상이다. 따라서, 식 (15)를 θ에 관한 식으로 다시 정리하면 다음과 같다.
식 (16)를 통해 빔을 조향하는 각도 θ는 주파수와 관련이 없는 TTD에 의해서 보정되는 [TeX:] $$\Delta \tau$$와 주파수에 의해서 변하는 PS에 의해서 보정되는 [TeX:] $$\Delta \phi$$에 따라 바뀌는 것을 알 수 있다. 따라서 식 (14)에서 대역폭에 의해서 결정되는 빔 스퀸트로 인해 조향할 수 있는 각도의 차이를 TTD에 의해서 더 넓힐 수 있다. 주파수 스캐닝 기술은 이러한 대역폭과 PS, 그리고 TTD로 관측하고자 하는 영역을 조향할 수 있게 먼저 설정하고 chirp 신호의 chirp rate에 따라 주파수별로 다른 방향으로의 빔을 이용하여 관측 영역을 스캔한다. 만약, down chirp을 사용한다면 높은 주파수에 의해 관측하고자 하는 영역의 가장 먼 지점부터 낮은 주파수에 의해 관측하고자 하는 영역의 가장 가까운 지점까지 송신 빔을 스캔하면서 신호를 송신한다. 이를 통해, 송신 신호의 펄스 폭을 적절하게 설정한다면 먼 곳부터 신호를 먼저 송신하기 때문에 그만큼 시간이 보정되어 수신할 때는 모든 관측 영역에서의 echo 신호가 거의 비슷하게 수신단에 도착한다. 이를 만족시키는 펄스 폭은 다음과 같이 얻어진다.
위 식에서, [TeX:] $$R_{f a r} \text { 와 } R_{n e a r}$$는 각각 가장 비행체로부터 관측 영역의 가장 먼 부분과 가장 가까운 부분까지의 거리를 나타낸다. Echo 신호를 수신할 때에는 송신할 때 스캔했던 방향과 반대 방향 즉, 앞의 예시처럼 down chirp을 사용하여 곳부터 가까운 곳을 스캔했다면 수신 시에는 가까운 곳부터 먼 곳으로 스캔하여 신호를 수신한다. 이러한 송수신 과정은 time-frequency (T-F) diagram을 통해 확인할 수 있다. 그림 2는 range 방향으로의 fast-time t와 range frequency 사이의 T-F diagram이다. 그림 1에서, 앞의 예시와 마찬가지로 down chirp을 가정하고 있으며 파란 실선이 이 down chirp 신호를 나타낸다. 이때 down chirp 신호의 chirp rate는 [TeX:] $$K_r$$이고 펄스 폭은 식 (17)과 같이 T라고 가정된다. 붉은색의 영역은 수신 시에 관측 영역을 빔 스퀸트를 통해 주파수에 따라 스캔하면서 시간에 따라 사용되는 주파수를 나타내고 전체 대역폭을 얼마의 시간동안 스캔할 것인지에 따라 수신 스캔 기울기 [TeX:] $$K_{f b c}$$가 결정된다. 우리는 이 수신 스캔 기울기를 steering rate이라고 정의하며 수신 시에 스캔하는 시간은 [TeX:] $$T_{f b c}$$로 정의된다. 이와 같이, 주파수 스캐닝 기술은 송수신 스캔이 서로 다른 부호의 기울기로 동작함으로써 거리에 따라 다른 수신 신호의 시간 지연을 보상해주게 되어 기존의 SAR보다 더 짧은 수신 window length를 가지게 된다. 그림(Fig.) 2. SAR raw data의 fast time-frequency diagram (Fast time-frequency diagram of the SAR raw data.) 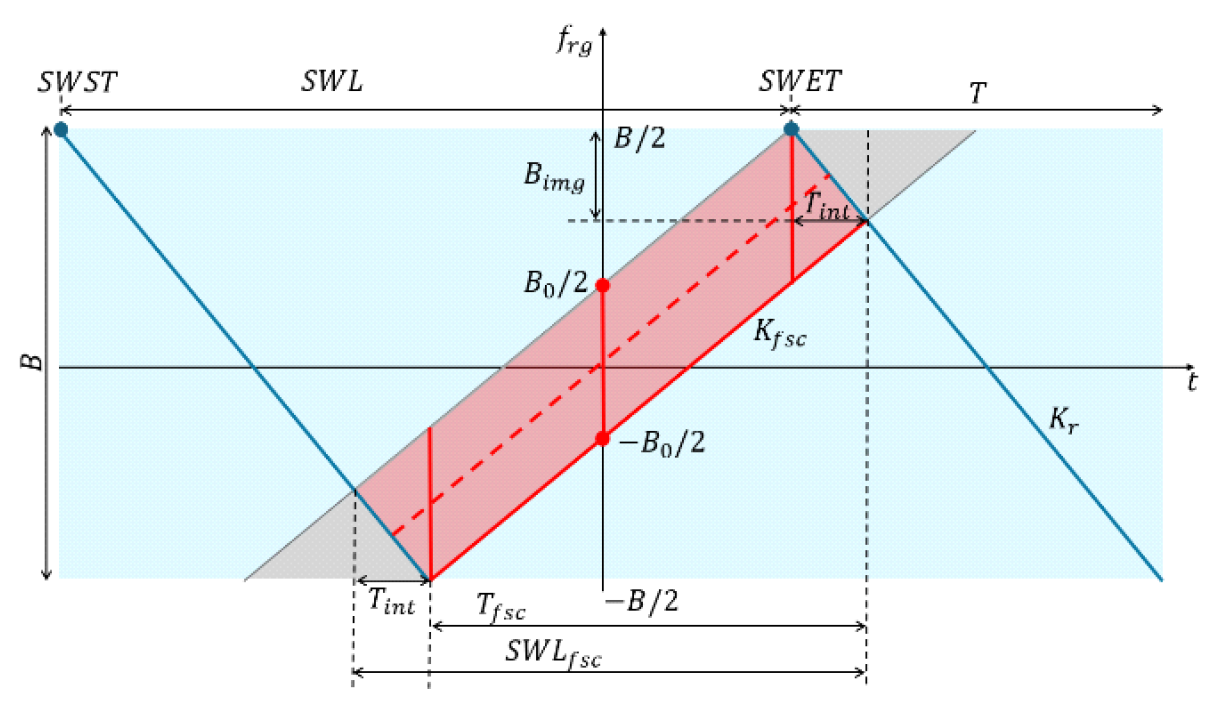 기존의 SAR와 같은 경우에는, 수신 window의 시작 시간과 끝 시간을 각각 sampling window start time (SWST)과 sampling window end time (SWET)이라고 했을 때, sampling window length (SWL)는 아래와 같이 계산된다.
따라서 실제로 반사되어 돌아오는 echo chirp 신호를 전부 수신해야 하기 때문에 수신을 위해 열어두는 window length는 SWL + T이 된다. 이와 달리, 원하는 range 방향의 해상도에 해당하는 대역폭을 [TeX:] $$B_{img}$$라고 했을 때, 주파수 스캐닝 기술을 이용하는 SAR 시스템의 SWST, SWET, 그리고 SWL는 각각 [TeX:] $$\operatorname{SWST}_{f s c}, \mathrm{SWET}_{fsco },$$ 그리고 [TeX:] $$\operatorname{SWL}_{f s c}$$로 정의되고 아래와 같이 계산된다.
또한, 주파수 스캐닝은 대역폭 전체를 관측 영역 전체에 송수신하는 기존의 SAR와 달리 특정 일부 관측 영역만을 그에 해당하는 주파수로 빔을 형성하여 송수신하기 때문에 주파수 빔이 특정 영역을 스캔하는 integration time은 다음과 같이 계산된다.
이 integration time은 steering rate 관점에서도 다음과 같이 계산될 수 있다.
이 때, [TeX:] $$B_0$$는 주파수 빔 폭이다. 이 주파수 빔 폭은 수신시에 주파수 별로 스캔할 때 실질적으로 각 sub-swath에 영향을 미치는 effective한 대역폭이므로 이 주파수 빔 폭이 원하는 range 방향으로의 해상도를 만족하기 위해서는 [TeX:] $$B_{img}$$보다 커야하며 식 (22)와 (23)이 같다는 것을 이용하여 [TeX:] $$B_{img}$$와 [TeX:] $$B_0$$ 사이의 다음과 같은 관계식을 유도할 수 있다.
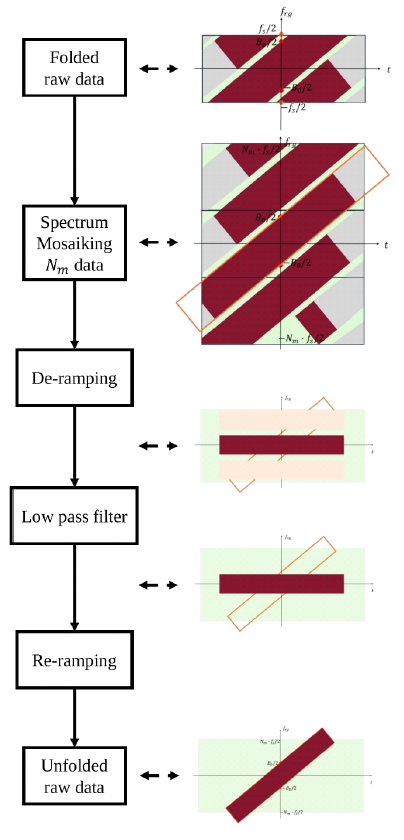
식 (24)에서, [TeX:] $$B_{img}$$에 곱해진 factor가 1보다 크기 때문에 [TeX:] $$B_0 \gt B_{i m g}$$가 만족된다. 실제로 데이터를 샘플링하는 샘플링 주파수 [TeX:] $$f_s$$는 aliasing을 피하기 위해 [TeX:] $$f_s \geq B_0$$여야되고 현실에서 구현할 때는 약간의 margin α를 두어 [TeX:] $$f_s=\alpha B_0$$로 보통 설정된다. 하지만, 모의 실험에서는 margin을 둘 필요가 없이 때문에 [TeX:] $$f_s=B_0$$로 설정한다. 하지만, 이러한 샘플링 주파수는 실제 송신 chirp 신호의 대역폭보다 작기 때문에 그림 3과 같이 데이터가 folding된다[28]. 따라서, 이미징을 위해서는 이 folding된 데이터를 펴주는 unfolding이라는 후처리 과정이 요구된다. 그림(Fig.) 3. 줄어든 샘플링 주파수로 얻은 SAR raw data의 fast time-frequency diagram (Fast time-frequency diagram of the SAR raw data using the reduced sampling frequency.) 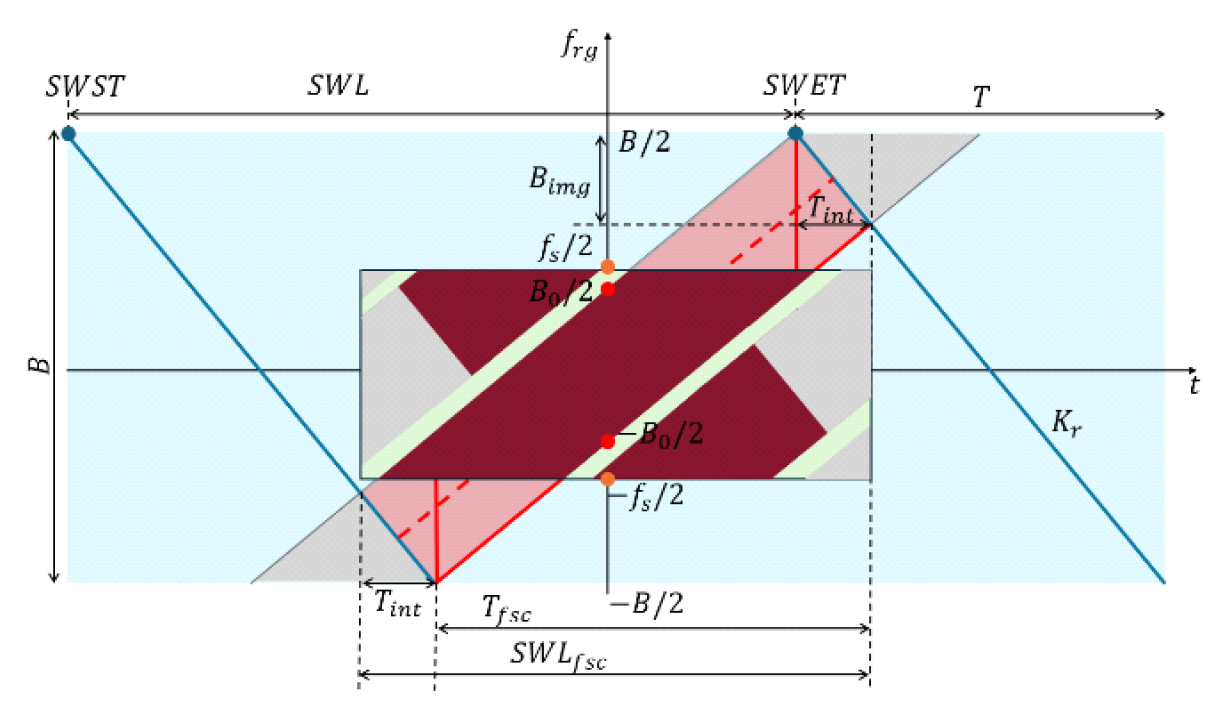 이 unfolding 과정은 그림 4와 같이 1) mosaiking, 2) de-ramping, 3) Low pass filter (LPF) 필터링, 그리고 4) re-ramping 이렇게 네 단계에 의해서 처리된다. 맨 먼저 mosaiking은 folding된 데이터를 주파수 축에서 양 옆으로 복사하는 과정이다. 시간 축에서는 데이터 사이사이에 0을 집어넣는 과정이다. 이 때, 주파수 축에서 복사되는 횟수는 다음과 같이 결정된다.
따라서, raw data는 range 방향으로 사이사이에 [TeX:] $$N_m-1$$개의 0이 interleaving된다. Mosaiking을 한 이후에는 시간에 따라 변하는 chirp 신호를 de-ramping을 통해 특정 peak frequency로 time-variant demodulation을 한다. De-ramping에 사용되는 함수는 다음과 같다.
위 식에서 t의 범위는 [TeX:] $$\left[-\mathrm{SWL}_{f s c} / 2, \mathrm{SWL}_{f s c} / 2\right]$$이다. De-ramping을 한 이후에는 folding 되었던 데이터들이 각 peak frequency만을 갖는 신호로 바뀌었기 때문에 주파수 축에서 서로를 구분할 수 있게 된다. 따라서, aliasing을 없애기 위해 LPF를 적용하여 원 신호만을 남기는 과정을 거친다. 이후에는 기존의 SAR와 같이 range 방향과 azimuth 방향으로의 compression을 하기 위해서 다시 re-ramping 과정을 거친다. Re-ramping은 de-ramping 신호의 켤레 복소수로 다음과 같다.
Re-ramping 과정까지 거치게 되면 그림 2와 같이 기존의 SAR와 같은 데이터를 얻을 수 있게 된다. 따라서, unfolding 과정을 거치고 난 이후에는 기존의 SAR에서처럼 range compression, range cell migration correction, 그리고 azimuth compression의 과정들을 거쳐 이미지를 얻을 수 있다. 비록 TTD와 추가적인 후처리 과정이 주파수 스캐닝 기술에는 요구되지만 기존 SAR보다 더 높은 해상도과 더 넓은 영역을 관측할 수 있게되고 여러 RF-chain이 포함된 sub-aperture 구조로 인해 하드웨어 전력과 같은 부담이 큰 SCORE에 비해 간단한 하드웨어 구조와 적은 수신 데이터량으로 인해 비교적 적은 메모리를 사용하여 이미징 과정을 처리할 수 있다. 하지만, TTD를 사용한다고 하더라도 effective한 대역폭 자체가 줄어들어 같은 range 방향으로의 해상도를 만족시키기 위해서는 그만큼 기존보다는 넓은 대역폭을 사용해야한다는 단점도 존재한다. 표 1은 이러한 SCORE와 주파수 스캐닝 기술의 장단점을 비교한 것이다. SAR 시스템을 디자인할 때, 표 1에서의 장단점을 기반으로 파라미터의 우선순위를 선정하여 그에 적절한 기술을 사용하는 것이 바람직하다. 표(Table) 1. SCORE와 주파수 스캐닝 기술의 장단점 비교 (Coparison of the advantages and disadvantages of SCORE and F-scan techniques.)
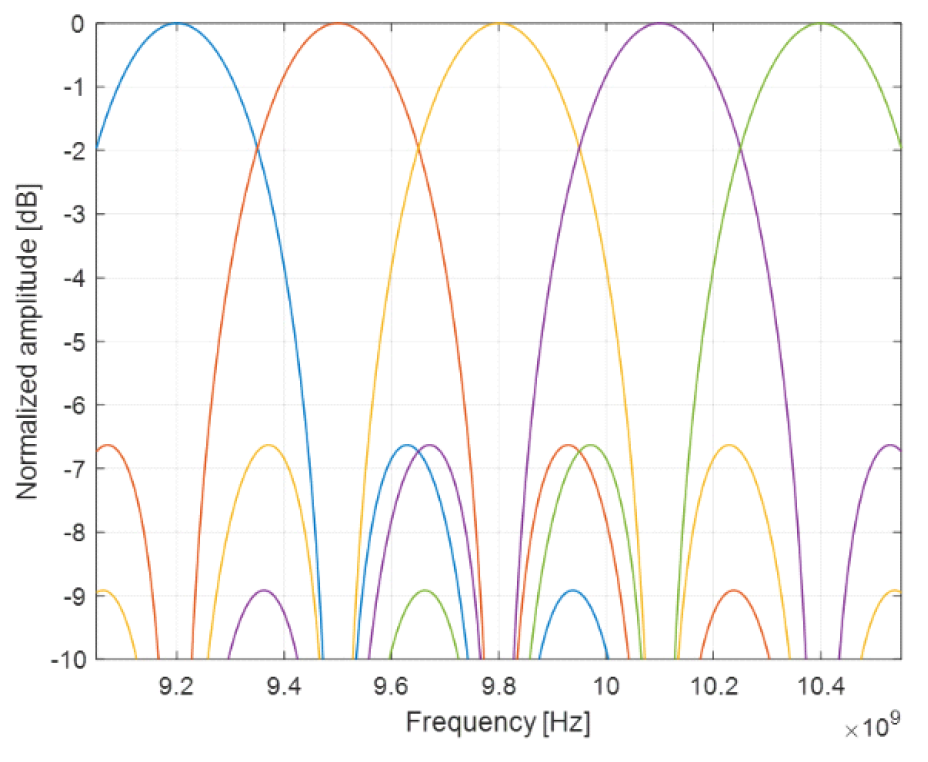
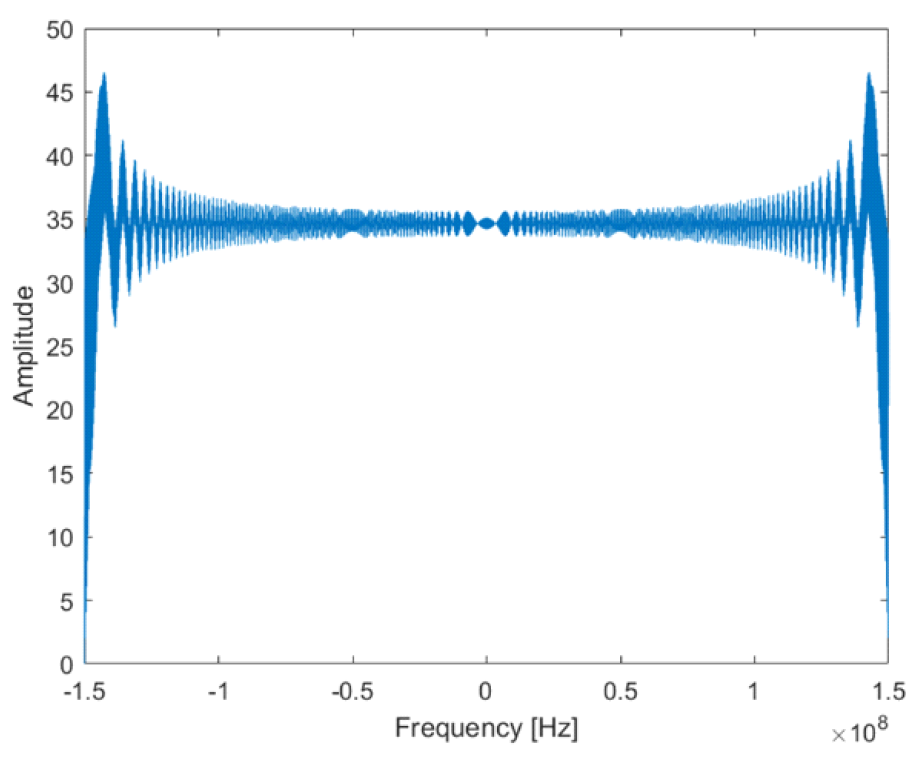
Ⅳ. 시뮬레이션 결과주파수 스캐닝 기술을 이용한 고해상도 광역관측 SAR 시스템의 이미징 성능을 확인하기 위하여 표 2와 3의 파라미터들이 사용된다. 표 3은 표 2의 파라미터들을 가지고 유도할 수 있는 파라미터들이다. 먼저, 표 2와 3의 파라미터들을 가지고 주파수 빔들의 분포와 T-F diagram을 확인할 수 있다. 그림 5와 6은 각각 표 2와 3의 파라미터들을 가지고 유도된 주파수 빔들의 분포와 T-F diagram을 나타낸다. 본 논문에서 사용되는 1.5 GHz의 chirp 대역폭에 대해서 1 m의 range 방향으로의 해상도를 얻기 위해서는 5개의 주파수 빔들이 각각 주파수 영역에서 300 MHz의 빔 폭을 가지고 range 방향의 sub-swath를 커버하게된다. 이때, 그림 5에서도 볼 수 있듯이 각 주파수 빔들은 중심 주파수가 서로 다르다. 따라서, 주파수 스캐닝 기술은 각 빔마다 해당되는 중심 주파수를 가지고 대상물들의 range 방향으로의 거리를 구분할 수 있다. 그림 6의 T-F diagram은 실제로는 그림 3과 같이 파란색 네모 박스 영역안에 빨간색 대각선 박스가 chirp 대역폭보다 작은 샘플링 주파수로 인해 aliasing이 발생하여 folding 현상이 발생하여야한다. 하지만, 편의상 본 논문에서는 그림 2와 같이 T-F diagram을 표현하였다. 표(Table) 2. SAR 파라미터 (SAR parameters.)
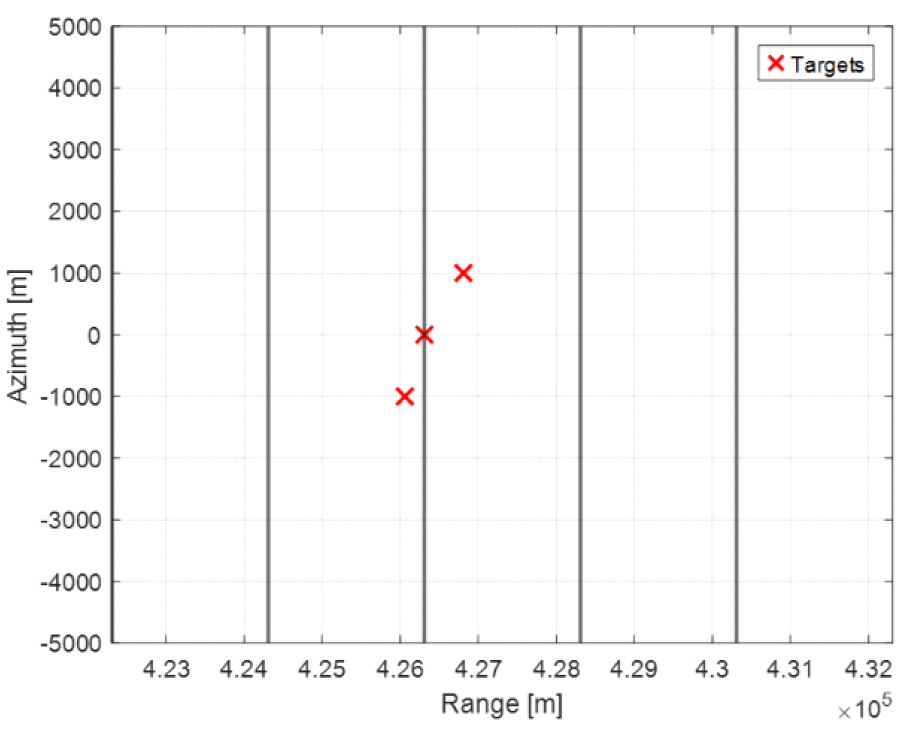
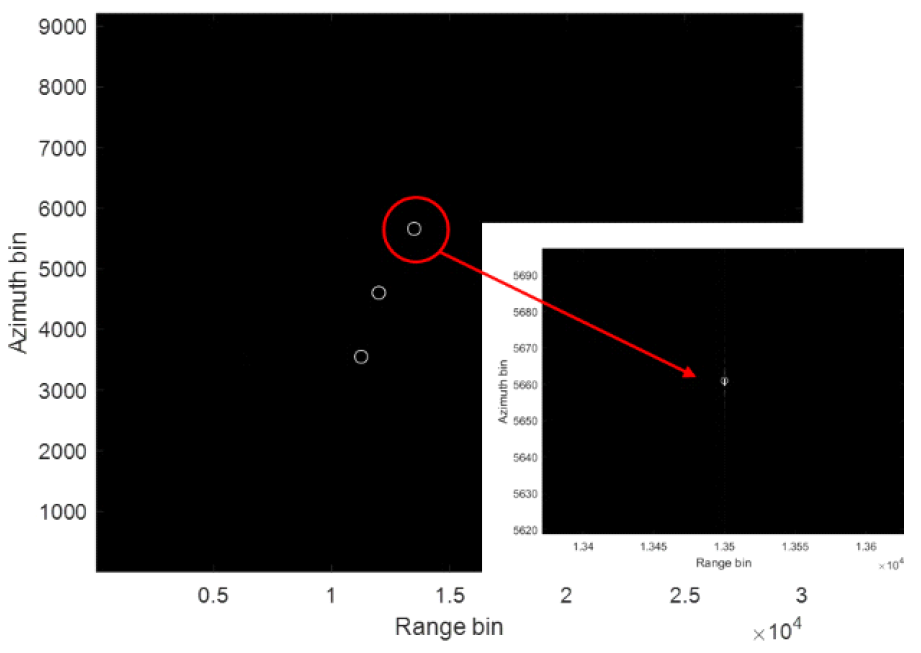
표(Table) 3. 유도된 SAR 파라미터 (Derived SAR parameters.)
그림(Fig.) 6. 표 1과 2의 파라미터들을 사용했을 때의 T-F diagram (T-F diagram based on the parameters in Tables 1 and 2.) 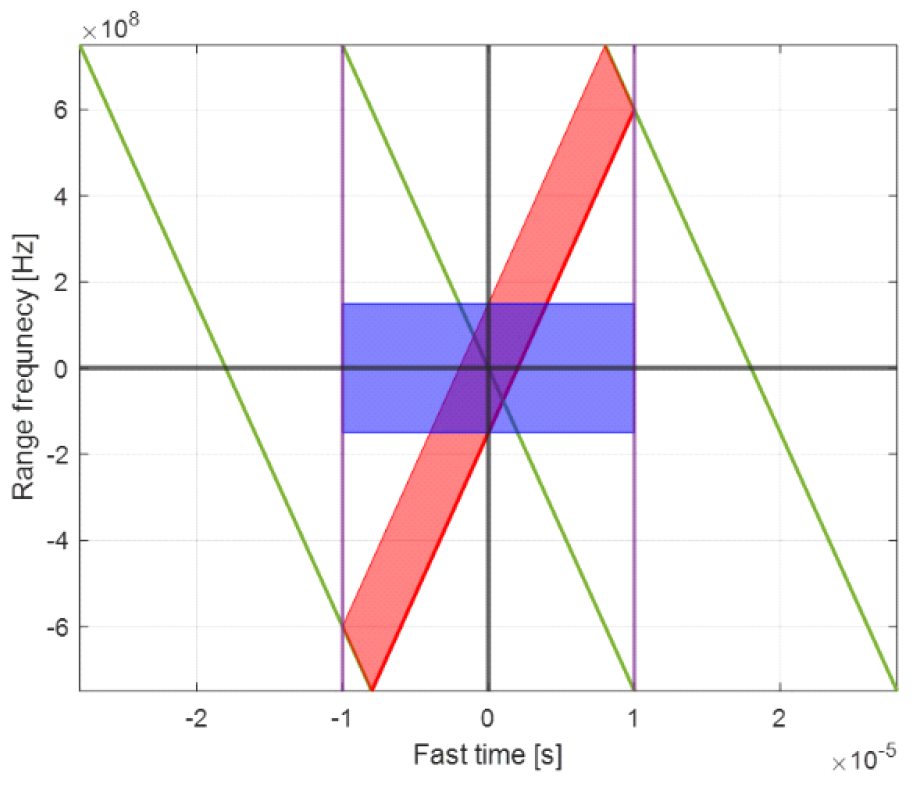 이러한 주파수 빔들의 분포와 T-F diagram을 토대로 그림 7과 같이 분포된 점 대상물들이 관측하고자 하는 영역에 있다고 가정했을 때 영상을 얻고자 한다. 이때, range cell migration은 보정되어 발생하지 않는다고 가정된다. 먼저, unfolding 과정의 필요성을 보기 위하여 unfolding 과정을 거치지 않은 folding 된 raw data를 가지고 그대로 영상을 처리하여 얻으면 그림 8과 9와 같이 얻어진다. 그림 8은 unfolding 과정을 거치지 않은 folded raw data를 그대로 range compression 했을 때의 결과이다. 주파수 스캐닝 기술은 각 대상물들의 echo 신호들이 중심 주파수가 서로 다르고 echo 신호를 전부 수신하는 것이 아닌 일부분만을 수신하기 때문에 그대로 range compression을 하게 되면 그림 8과 같이 제대로 range 방향으로 compression이 되지 않는다. 따라서, 그림 8에서의 결과를 토대로 azimuth compression을 하게 되면 range 방향으로 제대로 compression이 되지 않고 ambiguity가 발생하는 것을 확인할 수 있다. 따라서, 제대로된 이미지를 얻기 위해서는 unfolding 과정이 필수적으로 요구됨을 확인할 수 있다. 첫번째 대상물에 대하여 그림 10과 같이 raw data를 주파수 축에서 가지는 데이터에 대해서 각 unfolding 과정별 주파수 축에서의 결과는 그림 11과 같다. 그림 11에서의 unfolding 과정은 순서대로 (a) mosaiking, (b) de-ramping, (c) LPF filtering, 그리고 (d) re-ramping 과정을 나타낸다. 먼저, 그림 11-(a)에서의 mosaiking 과정을 통해 그림 10의 주파수 축에서의 raw data를 양 옆으로 복사한다. 이때 복사되는 횟수는 주파수 빔의 개수이다. 따라서, 그림 11-(a)는 그림 10의 그래프가 5번 반복된 그래프이다. 그 다음으로, 그림 11-(b)에서의 de-ramping 과정을 통해 넓은 대역폭의 신호를 특정 peak frequency의 신호로 변환해준다. 이 de-ramping 과정을 통해 그림 11-(a)에서의 신호가 그림 11-(b)에서와 같이 주파수 축에서 15개의 peak를 가지는 신호로 변환됨을 확인할 수 있다. De-ramping 과정을 거치고나면 이제 aliasing을 LPF를 통해 제거할 수 있으므로 원신호를 제외한 나머지 신호를 제거하기 위해서 LPF filtering을 하게된다. 이 과정은 그림 11-(c)와 같으며 5개의 peak가 있던 신호가 LPF를 통해 가운데 한 개의 peak만을 남겨두고 나머지 peak 성분들이 제거된 것을 확인할 수 있다. 마지막으로, 기존의 SAR에서처럼 range compression과 azimuth compression을 하기 위해서 신호를 다시 원상태로 돌리는 re-ramping 과정을 거치게 된다. 이 과정을 통해 하나의 주파수 성분으로 de-ramping 된 신호가 다시 chirp 신호와 같이 넓은 대역폭의 신호로 복구된다. 이렇게 re-ramping 과정까지 거치게 되면 folding되었던 데이터가 완전히 기존의 SAR 데이터와 같이 unfolding된다. 따라서, 이 후의 이미징 처리 과정은 기존의 SAR와 같이 range와 azimuth 방향에 대해서 compression을 그대로 수행하여 얻을 수 있다. 그림(Fig.) 8. Folded raw data를 이용하여 range compression을 했을 때의 결과 (Result of range compression using folded raw data.) 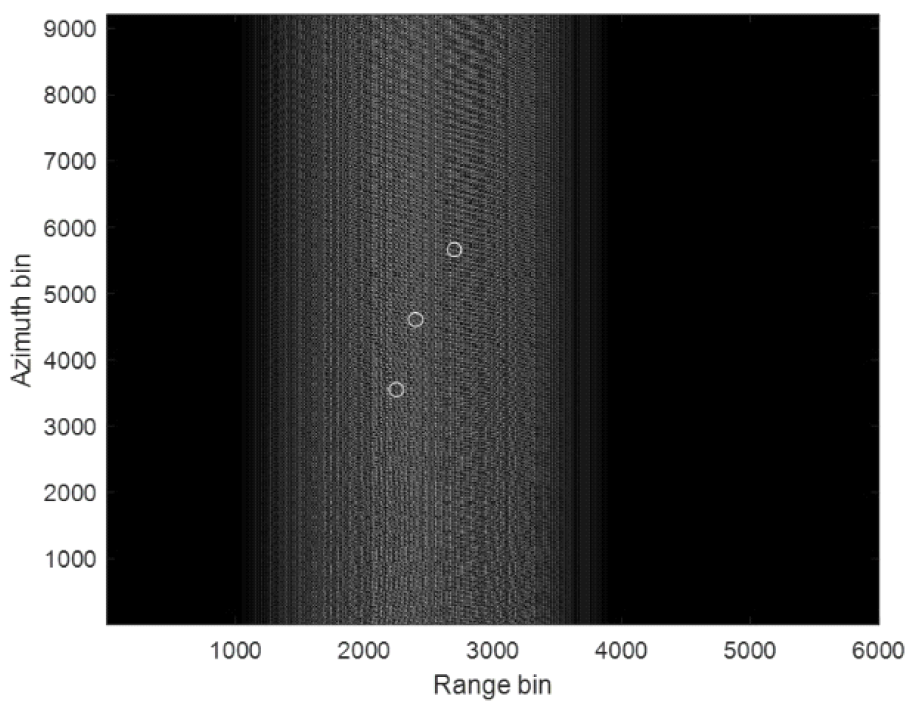 그림(Fig.) 9. Folded raw data를 이용하여 azimuth compression까지 했을 때의 이미지 결과 (Image result after azimuth compression using folded raw data.) 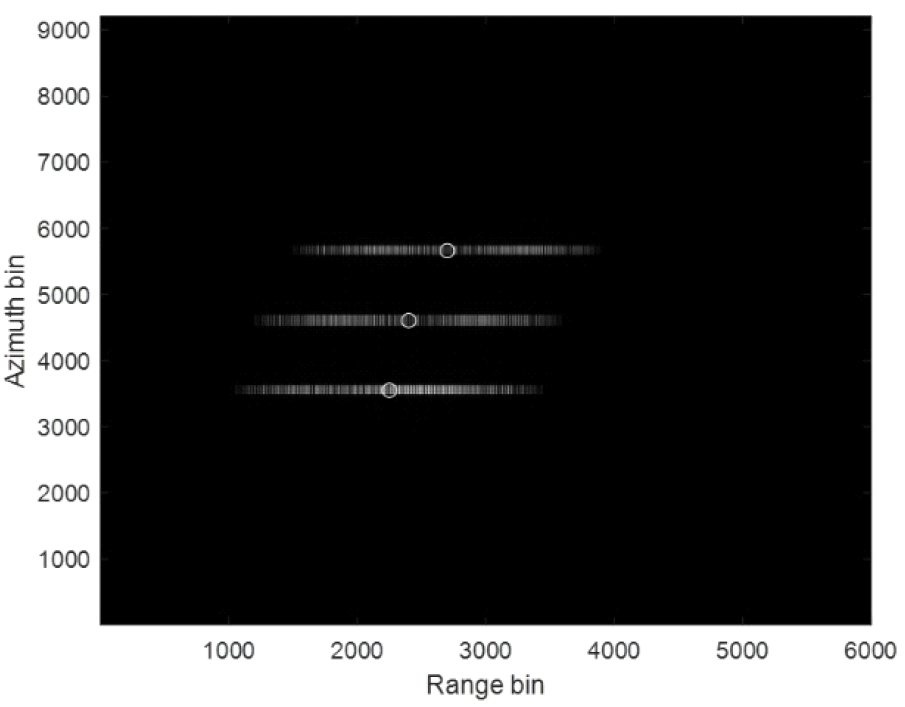 그림(Fig.) 11. 첫번째 대상물에 대한 주파수 축에서의 unfolding 과정 (a) Mosaiking, (b) De-ramping, (c) LPF filtering, and (d) Re-ramping (Unfolding process in the frequency domain for the first target (a) Mosaiking, (b) De-ramping, (c) LPF filtering, and (d) Re-ramping.) 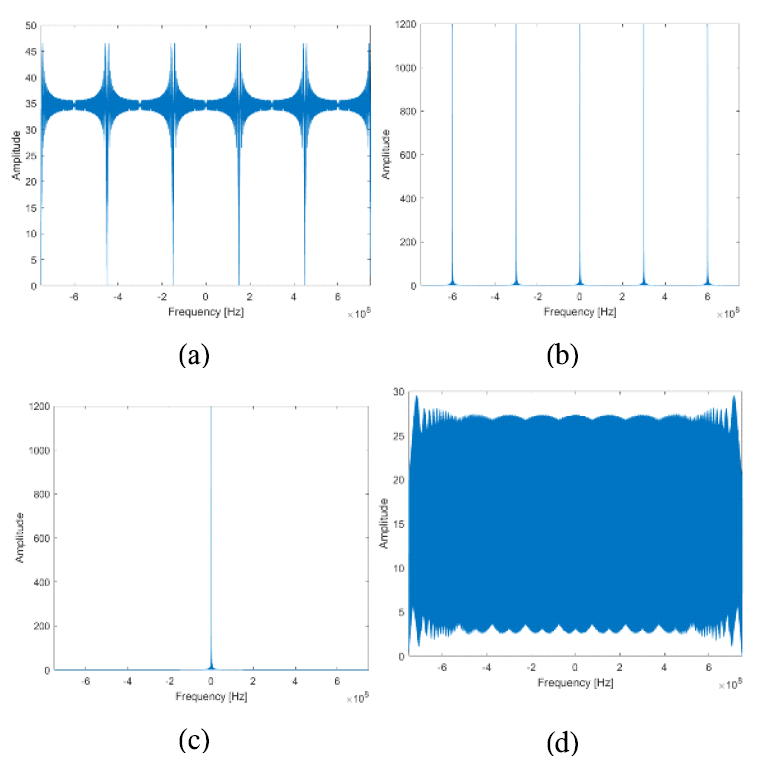 Unfolding 과정을 거친 후의 이미징 결과는 그림 12와 같다. 그림 12에서 오른쪽 아래의 이미지는 빨간색 동그라미로 표시된 대상물 주변을 확대하여 나타낸 이미지이다. Range 방향으로 compression이 되지 않던 그림 8과 9와 달리 그림 12에서의 unfoldig 과정을 거친 후의 raw data는 range 방향으로 완벽히 compression 되어 대상물의 range bin으로 에너지가 제대로 모여있음을 확인할 수 있다. 결과적으로, 주파수 스캐닝 기술을 이용한 고해상도 광역관측 SAR 시스템에서는 대상물을 맞고 돌아오는 echo 신호의 전부를 수신하는 것이 아닌 일부분만을 수신하기 때문에 그림 11과 같은 unfolding 과정이 필수적으로 요구되는 것을 확인할 수 있다. Ⅴ. 결 론궂은 날씨나 육안으로 확인할 수 없는 어두운 환경에서도 고해상도로 이미지를 형성할 수 있는 SAR 시스템은 계속해서 더 높은 해상도와 넓은 관측 영역을 요구하지만 SAR 시스템의 내재적인 한계로 인해 두 요구조건을 동시에 만족시키는 것이 불가능하다. 따라서, 이를 해결하기 위한 방법으로 디지털 빔포밍을 이용한 MAPS나 SCORE와 같은 기술이 개발되었지만 여러개의 RF-chain으로 구성된 다수의 sub-aperture 구조로 안테나 배열을 구성해야하여 하드웨어가 복잡해지고 그만큼 구현에 많은 부담이 발생한다는 단점이 존재한다. 하지만, 주파수 스캐닝 기술은 기존의 SAR 시스템과 같이 단일 RF-chain 구조로 간단하게 하드웨어를 구성할 수 있으면서 SCORE의 장점은 그대로 취할 수 있는 기술이다. 또한, 이외에도 대상물에 맞고 반사되는 echo 신호를 전부 수신하는 것이 아니라 일부만을 수신하여 가뜩이나 고해상도 광역관측에 의해 많아진 데이터의 양을 줄여서 onboard의 부담을 확 줄일 수 있다. 따라서, 주파수 스캐닝 기술이 SCORE의 대체 기술로 많은 관심을 받고 있으며 본 논문에서는 튜토리얼로써 먼저 SAR 시스템 구현을 위해 요구되는 PRF의 범위를 통해 왜 주파수 스캐닝과 같은 기술이 필요한지를 설명하고 주파수 스캐닝 기술의 원리와 필수적으로 요구되는 후처리 과정인 unfolding 과정을 리뷰하였다. 마지막으로, 모의 실험을 통해 folding된 데이터로 이미징한 결과와 비교함으로써 unfolding 과정을 거치지 않으면 제대로된 이미지를 형성할 수 없다는 것을 실험 결과를 통해 입증하였다. BiographyBiographyBiographyBiography이 남 윤 (Namyoon Lee)2006년 2월: 고려대학교 전파통신공학 학사 2008년 2월: 한국과학기술원 전자공학 석사 2014년 12월: The University of Texas at Austin, Department of Electrical and Computer Engineering 박사 2008년 2월~2011년 6월: 삼성종합기술 연구원/선임연구원 2014년 11월~2015년 5월: NOKIA Research Center, Berkeley, USA 선임연구원 2015년 5월~2016년 2월: Intel Labs, Santa Clara, USA Researcher Scientist 2016년 2월~2022년 2월: POSTECH 조교수/부교수 2022년 3월~2025년 2월: 고려대학교 부교수/교수 2025년 3월~현재: POSTECH 교수 <관심분야> 차세대 MIMO 송/수신기, 기계학습기반 통신 네트워크 설계 References
|
StatisticsCite this articleIEEE StyleJ. Yim, D. Kim, I. Ban, N. Lee, "Review on High Resolution Wide Swath SAR System Using Frequency Scanning," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1617-1630, 2025. DOI: 10.7840/kics.2025.50.10.1617.
ACM Style Jungbin Yim, Donghyun Kim, Inmo Ban, and Namyoon Lee. 2025. Review on High Resolution Wide Swath SAR System Using Frequency Scanning. The Journal of Korean Institute of Communications and Information Sciences, 50, 10, (2025), 1617-1630. DOI: 10.7840/kics.2025.50.10.1617.
KICS Style Jungbin Yim, Donghyun Kim, Inmo Ban, Namyoon Lee, "Review on High Resolution Wide Swath SAR System Using Frequency Scanning," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1617-1630, 10. 2025. (https://doi.org/10.7840/kics.2025.50.10.1617)
|