IndexFiguresTables |
Donghun Lee♦°Secrecy Rate Analysis of Dual-Hop Triple Selection AF Relaying Over Nakagami Fading ChannelsAbstract: This paper analyzes the secrecy rate of dual-hop triple selection amplify-and-forward (AF) relaying over Nakagami fading channels. The triple selection chooses transmit antenna, relay node and user node with the maximum received signal to noise ratio (SNR) using feedback information from each node. In this study, we use selection combing (SC) and maximum ratio combining (MRC) to derive new exact closed-form expressions for the cumulative distribution function (CDF) and probability density function (PDF) of the received SNR for triple selection. To derive the secrecy rate, this paper presents the alternative exact analytical expressions for CDF and PDF using fractional and calculus mathematics. Using the alternative distribution, this work evaluates new exact and approximate analytical expressions of the triple selection for the secrecy rate. Using the asymptotic analysis, the power offset and the slope are quantified for the secrecy rate. Using asymptotic and numerical results, we demonstrate that the high SNR slope for the secrecy rate is constant regardless of authorizer’s parameters and eavesdropper’s parameters as well as fading index of channel. We also confirm that the high SNR power offset is affected by the parameters of the authorizer and the eavesdropper, whereas the fading index is not affected. Keywords: Triple selection , amplify and forward (AF) , relay , Nakagami fading channels Ⅰ. IntroductionRapid advances in wireless communication technologies and network deployments have resulted in a surge in the amount of mobile traffic worldwide in the past few years[1]. As the importance of information security increases due to the increase in mobile traffic, interest in information security transmission technology is increasing. In particular, physical layer security (PLS) is emerging as an attractive technology that improves information security performance with low computational complexity by using the random characteristic of a channel[2,3]. Transmit antenna selection using multiple antennas in [4]-[7] is a promising technology, which provides the transmit spatial diversity with low-computational complexity. Alves et al.[8] derived exact analytical xpression of the transmit antenna selection for the secrecy outage probability using wiretap channel model introduced in the previous work[9] and they considered single radio frequency (RF) chain at transmitter and receiver. Yang et al.[10] derived analytical expression of the transmit antenna selection for various secrecy performance (i.e., the probability of non-zero secrecy rate and the secrecy outage probability) over Nakagami fading channels. The work considered selection combining (SC) and maximal ratio combining (MRC) which employs multi-RF chains at receiver. Wang et al.[11] proposed combination of the transmit antenna selection and generalized selection combining (GSC) for secrecy communication. They derived analytical solution of the transmit antenna selection with GSC for the secrecy performance over Nakagami fading channels. Lee et al.[12] proposed combination of the user and transmit antenna selection and derived the explicit formula of the combined scheme for the secrecy outage probability over arbitrary Nakagami fading channels which contains the integer and real-valued fading indices. Since the secrecy performance analysis for generalized channel is important, the previous works[13-15] analyzed the secrecy performance over various generalized channels. Yang et al.[13] considered η − μ fading channels which include Rayleigh, Nakagami, and Hoyt fading channels[16]. They derived mathematical expression of the transit antenna selection with MRC for the secrecy outage probability and studied the impact of co-channel interference on the secrecy outage probability. Moualeu et al.[14] researched the performance analysis of the antenna selection under generalized α − ㅡ μ fading channels. They derived analytical expressions of the transmit antenna selection for the lower bound of the secrecy outage probability and the secrecy rate. Sanchez et al.[15] researched the performance analysis of the transmit antenna selection under κ− ㅡ μ fading channels. They derived mathematical expressions of the antenna selection for the secrecy outage probability and the secrecy rate. The works[17-23] investigated the impact of channel imperfection (i.e., feedback delay, correlation and channel estimation error) on the secrecy performance. The effect of feedback delay on the secrecy performance was studied in the previous works[17-19]. Ferdinand et al.[17]. derived the closed-from expression of the antenna selection for the secrecy performance where they considered single antenna at receiver. Xiong et al.[18]. derived explicit formulas of the transmit antenna selection with MRC for the probability of non-zero secrecy rate and the secrecy outage probability in presence of feedback delay. Huang et al.[19]. researched the secrecy analysis of the generalorder antenna selection under feedback delay. They derived the analytical expressions of the selection scheme for the various secrecy performance. The works[20-22] investigated the effect of the correlation on the secrecy performance of the transmit antenna selection. Yang et al.[20]. derived the analytical solution of the transmit antenna selection with MRC for the secrecy outage probability and analyzed the impact of the antenna correlation on the secrecy performance. Si et al.[21] considered both the antenna correlation and the channel correlation and analyzed the secrecy outage probability of the transmit antenna selection with MRC over correlated Nakagami fading channels. Si et al.[22]. presented the secrecy outage probability analysis of the transmit antenna selection over correlated Rayleigh fading channels where MRC, SC and equal gain combining (EGC) are considered as a diversity combining scheme. Lee et al.[23]. analyzed the impact of channel estimation error on the secrecy performance. The work developed the closed-form expressions of combining the user and antenna selection for both the secrecy outage probability and the probability of non-zero secrecy rate under channel estimation error. Dual-hop amplify and forward (AF) relaying[24-27] has received considerable attention due to its promising potential to increase coverage and improve secrecy performance with low-computational complexity. For this reason, the works[28-33] investigated the secrecy performance analysis of the dual-hop AF relaying. The previous works[28-30] studied the effect of various fading channels on the secrecy performance of the AF relaying. Jindal et al.[28] evaluated bound expressions of the dual-hop AF relaying for the secrecy outage probability over Rayleigh fading channels. They analyzed the effect of the relay selection without eavesdropper’s channel state information (CSI) on the secrecy performance. Lee et al.[29] presented the secrecy performance analysis of combination of the antenna, relay and user selection (i.e., triple selection) over Nakagami fading channels. The work derived the lower bound expression of the triple selection for the secrecy outage probability where two popular combining schemes (i.e., MRC and SC) are considered. Shahriyer et al.[30] studied the relay selection strategy to improve secrecy performance in dual-hop AF relaying over κ − μ shadow-fading channels. They derived the analytical expressions for various secrecy performance such as the probability of non-zero secrecy rate, the secrecy outage probability and the secrecy rate over κ − μ shadow-fading channels. The previous works[31-33] researched the impact of channel imperfection (i.e., cochannel interference, correlation, and feedback delay) on the secrecy performance in dual-hop AF relaying. Fan et al.[31] investigated the effect of co-channel interference of AF relaying on the secrecy performance. They evaluated the lower bound expression of the relay selection for the secrecy outage probability where two selection criteria using instantaneous and statistical channel information were utilized. Fan et al.[32] analyzed the secrecy outage probability of the transmit antenna selection at source node and relay selection at relay node over correlated fading channels where full and partial relay selection criteria were used. The work[33] presented the effect of outdated CSI on the secrecy performance of the joint relay and jammer selection in dual-hop AF relaying. Table 1. Summary of related works
1.1 MotivationWhen the authorizer has CSI of eavesdropper, the secrecy rate is a principle secrecy performance metric[11,14,15,30]. Even if the previous work[29] investigated the secrecy outage probability of the triple selection, the author has no attention to study the secrecy rate over Nakagami fading channels. For this reason, this work presents the secrecy rate analysis of the dual-hop triple selection over Nakagami fading channels where MRC and SC are considered as a combining scheme. 1.2 Contributions· The first contribution of this work is to develop new exact closed-form expressions for the cumulative distribution function (CDF) and probability density function (PDF) of the received signal to noise ratio (SNR) for the triple selection using MRC and SC over Nakagami fading channels which include the modified Bessel function. This study also presents alternative exact analytical expressions for the CDF and PDF using fractional and calculus mathematics which is the second contribution. Using the alternative distribution, this work evaluates new exact and approxi-mate analytical expressions of the triple selection for the secrecy rate, which is the final contribution. Using the approximate expression, the high SNR slope and the high SNR power offset of the secrecy rate are quantified for the triple selection with MRC and SC · From the asymptotic analysis, this study shows that the slope of the triple selection is one regardless of combining method. This means that the slope is independent to the authorizer’s parameters, the eavesdropper’s parameters, and the channel parameters. From the numerical results, we find that the fading index of the channels such as the authorizer channel and the eavesdropper channel has no effect on the slope and the power offset of the secrecy rate. Additionally, the parameters of the authorizer, such as the number of antennas and nodes of relays and user nodes, can improve the secrecy rate by reducing the power offset. Oppositely, eavesdropper’s parameters such as the number of receive antennas can degrade the secrecy rate by increasing the high SNR power offset. This work is organized as follows: Section II presents overview of the triple selection in the dual-hop AF relaying over Nakagami fading channels. Section III and Section IV analyze the secrecy rate of the triple selection. Section V concludes this paper. Ⅱ. System Overview
Table 1. 표 설명
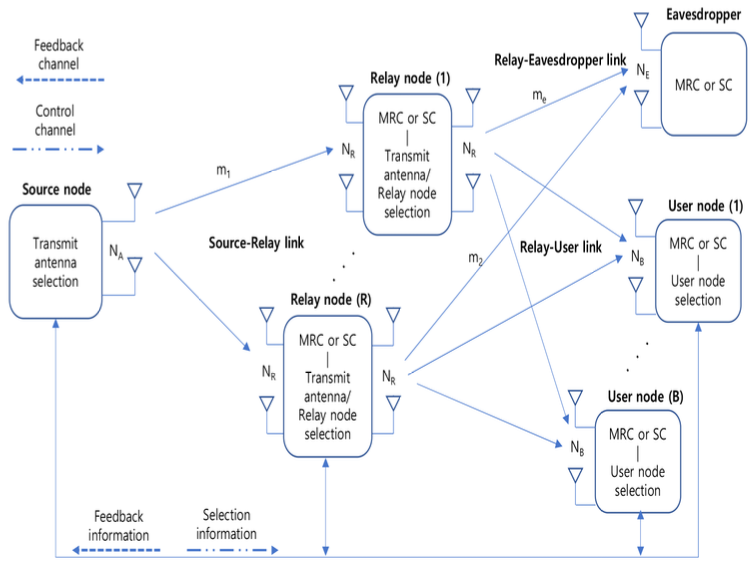
This work analyzes the secrecy performance of the dual-hop triple selection AF relaying as shown in Fig.1. The triple scheme selects relay node, user node and transmit antenna which provides the largest received SNR from the user and relay nodes. The triple selection is performed at the source node using feedback information from each relay and user node. In this study, MRC and SC are considered as a combining technique used in wireless communication system to improve signal quality. MRC combines signals from multiple antennas, weighting each signal based on its instantaneous channel gain to maximize the received SNR. SC selects the signal from the antenna with the highest SNR and uses its signal. For SC, feedback information contains the largest SNR value of each node and its transmit/receive antenna index. In the case of MRC, the feedback information contains the largest SNR value of each node and its transmit antenna index. Since this study considers Nakagami fading channels, the fading indices for the source-relay link, the relay-user link and the relay-eavesdropper link are denoted by m1, m2 and me, respectively. Further, the average SNR at relay node, user node and eavesdropper are denoted by [TeX:] $$\bar{\gamma}_1, \bar{\gamma}_2 \text { and } \bar{\gamma}_{\mathrm{e}}$$. This work considers multiple antennas at each node and eavesdropper. For this reason, single source node has NA transmit antennas, the R relay node has NR receive/transmit antennas and the B user node has NB receive antennas. Single eavesdropper has NE receive antennas. This work assumes the perfect channel estimation and no feedback delay. When the fading index is denoted by mand the number of received antennas is denoted by N, CDF and PDF of the received SNR for MRC over Nakagami fading channels are given by[10,29]
(1)[TeX:] $$F_{\mathrm{mc}}(\gamma)=1-e^{-m \frac{\gamma}{\bar\gamma}} \sum_{i=0}^{m \mathrm{~N}-1} \frac{\left(m \frac{\gamma}{\bar\gamma}\right)^i}{i!},$$and
(2)[TeX:] $$f_{\mathrm{mc}}(\gamma)=\frac{m}{\bar{\gamma}} \cdot \frac{\left(m \frac{\gamma}{\bar{\gamma}}\right)^{m \mathrm{~N}}}{(m \mathrm{~N}-1)!} e^{-m \frac{\gamma}{\bar\gamma}},$$where [TeX:] $$\bar{\gamma}$$ denotes the average SNR per antenna. Similarly, the distribution of the received SNR for SC over Nakagami fading channels is given by[10,29]
(3)[TeX:] $$F_{\mathrm{sc}}(\gamma)=\left[1-e^{-m \frac{\gamma}{\bar\gamma}} \sum_{i=0}^{m-1} \frac{\left(m \frac{\gamma}{\bar\gamma}\right)^i}{i!}\right]^{\mathrm{N}},$$and
(4)[TeX:] $$\begin{gathered} f_{\mathrm{sc}}(\gamma)=\mathrm{N} \frac{m^m}{\bar{\gamma}} \cdot \frac{\left(m \frac{\gamma}{\bar{\gamma}}\right)^{m-1}}{(m-1)!} e^{-m \frac{\gamma}{\bar\gamma}} \\ \times\left[1-e^{-m \frac{\gamma}{\bar\gamma}} \sum_{i=0}^{m-1} \frac{\left(m \frac{\gamma}{\bar{\gamma}}\right)^i}{i!}\right]^{\mathrm{N}-1} \end{gathered}$$Ⅲ . Secrecy Rate Analysis3.1 Distribution of triple selection3.1.1 MRC The triple scheme selects the transmit antenna and the receive node with the maximum received SNR. Using order statistic[34] , PDF and CDF of the received SNR for the transmit antenna and node selection with MRC can be derived by using Eq.(1) and Eq.(2)
(5)[TeX:] $$F_{\mathrm{s}, \mathrm{mc}}(\gamma)=\left[F_{\mathrm{mc}}(\gamma)\right]^{\mathrm{DM}}$$and
(6)[TeX:] $$f_{\mathrm{s}, \mathrm{mc}}(\gamma)=\mathrm{DM}\left[F_{\mathrm{mc}}(\gamma)\right]^{\mathrm{DM}-1} f_{\mathrm{mc}}(\gamma)$$where M is the number of transmit antennas at transmitter side and D is the number of nodes at receiver side. Using binomial expansion, Eq.(1) can be rewritten by
(7)[TeX:] $$F_{\mathrm{mc}}(\gamma)=\sum_{p=0}^1 \sum_{i=0}^{p(m \mathrm{~N}-1)}(-1)^p e^{-p m \frac{\gamma}{\bar\gamma}} \frac{\left(m \frac{\gamma}{\bar\gamma}\right)^i}{i!} .$$By substituting Eq.(7) into Eq.(5), CDF of the received SNR for the node and transmit antenna selection with MRC can be obtained by
(8)[TeX:] $$F_{\mathrm{s}, \mathrm{mc}}(\gamma)=\sum_{P_{\mathrm{s}, \mathrm{DM}}} \sum_{I_{\mathrm{s}, \mathrm{DM}}} \Delta_{\mathrm{s}, \mathrm{mc}}\left(m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{b_{\mathrm{s}, \mathrm{mc}}} e^{-a_{\mathrm{s}, \mathrm{mc}} m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}}$$where [TeX:] $$a_{\mathrm{s}, \mathrm{mc}}=\sum_{j=1}^{\mathrm{DM}} p_{\mathrm{s}, j}, b_{\mathrm{s}, \mathrm{mc}}=\sum_{j=1}^{\mathrm{DM}} i_{\mathrm{s}, j} . \sum_{P_{\mathrm{DM}}}$$ and [TeX:] $$\sum_{I_{\mathrm{DM}}}$$ denote (DM)-fold summations given by
(9)[TeX:] $$\sum_{P_{\mathrm{s}, \mathrm{DM}}}=\sum_{p_{\mathrm{s}, 1}=0}^1 \cdots \sum_{p_{\mathrm{s}, \mathrm{DM}}=0}^1$$
(10)[TeX:] $$\sum_{I_{\mathrm{s}, \mathrm{DM}}}=\sum_{i_{\mathrm{s}, 1}=0}^{p_{\mathrm{s}, 1}\left(m_{\mathrm{s}} \mathrm{~N}-1\right)} \cdots \sum_{i_{\mathrm{s}, \mathrm{DM}}=0}^{p_{\mathrm{s}, \mathrm{DM}}\left(m_{\mathrm{s}} \mathrm{~N}-1\right)}$$and
(11)[TeX:] $$\Delta_{\mathrm{s}, \mathrm{mc}}=\frac{(-1)^{a_{\mathrm{s}, \mathrm{mc}}}}{\prod_{j=1}^{\mathrm{DM}}\left(i_{\mathrm{s}, j}\right)!}$$where s = 1 for the source-relay link and s = 2 for the relay-user link. Similarly, PDF is given by substituting Eq.(2) and Eq.(7) into Eq.(6)
(12)[TeX:] $$\begin{array}{r} f_{\mathrm{s}, \mathrm{mc}}(\gamma)=\sum_{P_{\mathrm{s}, \mathrm{DM}-1} l_{\mathrm{s}, \mathrm{DM}-1}} \nabla_{\mathrm{s}, \mathrm{mc}}\left(\frac{m_{\mathrm{s}}}{\bar{\gamma}_{\mathrm{s}}}\right) \\ \quad \times\left(\frac{m_{\mathrm{s}} \gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{\eta_{\mathrm{s}, \mathrm{mc}}-1} e^{-\left(c_{\mathrm{s}, \mathrm{mc}}+1\right) \frac{m_{\mathrm{s}} \gamma}{\bar{\gamma}_{\mathrm{s}}}} \end{array}$$where [TeX:] $$\eta_{\mathrm{s}, \mathrm{mc}}=d_{\mathrm{s}, \mathrm{mc}}+m_{\mathrm{s}} \mathrm{~N}$$ and [TeX:] $$c_{\mathrm{s}, \mathrm{mc}}=\sum_{j=1}^{\mathrm{DM}-1} p_{\mathrm{s}, j}$$, [TeX:] $$d_{\mathrm{s}, \mathrm{mc}}=\sum_{j=1}^{\mathrm{DM}-1} i_{\mathrm{s}, j}$$. [TeX:] $$\sum_{P_{\mathrm{DM}-1}}$$ denote (DM−1)-fold summations given by
(13)[TeX:] $$\sum_{P_{\mathrm{s}, \mathrm{DM}-1}}=\sum_{p_{\mathrm{s}, 1}=0}^1 \ldots \sum_{p_{\mathrm{s}, \mathrm{DM}-1}=0}^1$$
(14)[TeX:] $$\sum_{I_{\mathrm{s}, \mathrm{DM}-1}}=\sum_{i_{\mathrm{s}, 1}=0}^{p_{\mathrm{s}, 1}\left(m_{\mathrm{s}} \mathrm{~N}-1\right)} \cdots \sum_{i_{\mathrm{s}, \mathrm{DM}}=0}^{p_{\mathrm{s}, \mathrm{DM}-1}\left(m_{\mathrm{s}} \mathrm{~N}-1\right)}$$and
(15)[TeX:] $$\nabla_{\mathrm{s}, \mathrm{mc}}=\mathrm{DM} \frac{(-1)^{c_{\mathrm{s}, \mathrm{mc}}}}{\prod_{j=1}^{\mathrm{DM}-1}\left(i_{\mathrm{s}, j}\right)!\left(m_{\mathrm{s}} \mathrm{~N}-1\right)!} .$$Similar to the works[35,36], when instantaneous received SNRs of the source-relay link and the relay-user link are denoted by γ1 and γ2, CDF of the received SNR for the triple selection with MRC is given by
(16)[TeX:] $$\begin{aligned} & F_{\mathrm{t}, \mathrm{mc}}(\gamma)=P\left(\frac{\gamma_1 \gamma_2}{\gamma_1+\gamma_2} \leq \gamma\right) \\ = & \int_0^{\infty} P\left(\frac{\gamma_1 x}{\gamma_1+x} \leq \gamma\right) f_{2, \mathrm{mc}}(x) d x \\ = & \int_0^\gamma f_{2, \mathrm{mc}}(x) d x+\int_\gamma^{\infty} F_{1, \mathrm{mc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{mc}}(x) d x \end{aligned}$$where F1,mc(γ) with D = R, M = NA, N = NR, s= 1 presents CDF for transmit antenna and relay node selection with MRC in source-relay link. f2,mc(γ) with D = B, M = NR, N = NB, s = 2 presents PDF for the transmit antenna and user node selection with MRC in relay-user link. Since Eq.(8) can be rewritten by
(17)[TeX:] $$\begin{aligned} F_{\mathrm{s}, \mathrm{mc}}(\gamma)=1 & +\sum_{p_{\mathrm{s}, j} \notin \text { all zero } I_{\mathrm{s}, \mathrm{DM}}} \triangle_{\mathrm{s}, \mathrm{mc}} \\ & \times\left(m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{b_{\mathrm{s}, \mathrm{mc}}} e^{-a_{\mathrm{s}, \mathrm{mc}} m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}}, \end{aligned}$$CDF of the received SNR for the triple selection is obtained by substituting Eq.(12) and Eq.(17) into Eq.(16)
(18)[TeX:] $$\begin{gathered} F_{\mathrm{t}, \mathrm{mc}}(\gamma)=1+\int_\gamma^{\infty} F_{1, \mathrm{mc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{mc}}(x) d x \\ =1+\sum_{\mathrm{F}, \mathrm{mc}} \Delta_{1, \mathrm{mc}} \nabla_{2, \mathrm{mc}}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{b_{1, \mathrm{mc}}}\left(\frac{\gamma}{\bar{\gamma}_2}\right)^{\eta_{2, \mathrm{mc}}} \\ \times \int_0^{\infty}\left(\frac{\gamma(\gamma+z)}{z}\right)^{b_{1, \mathrm{mc}}}(\gamma+z)^{\eta_{2, \mathrm{mc}}-1} \\ \times e^{-a_{1, \mathrm{mc}} \frac{m_1}{\bar{\gamma}_1} \frac{\gamma(\gamma+z)}{z}} e^{-\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\bar{\gamma}_2}(\gamma+z)} d z \end{gathered}$$where
(19)[TeX:] $$\sum_{\mathrm{F}, \mathrm{mc}}=\sum_{p_{1, j} \notin \text { all }} \sum_{\text {zero } I_{1, \mathrm{RN}_{\mathrm{A}}}} \sum_{P_{2, \mathrm{UN}_{\mathrm{R}}-1}} \sum_{I_{2, \mathrm{UN}_{\mathrm{R}}-1}} .$$Using binomial expansion and integral function[37], Eq.(3.471.9), the exact closed-form CDF expression for the triple selection with MRC is given by
(20)[TeX:] $$\begin{gathered} F_{\mathrm{t}, \mathrm{mc}}(\gamma)=1+2 \sum_{\mathrm{F}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{mc}}}\binom{\eta_{\mathrm{F}, \mathrm{mc}}}{k} \Xi_{\mathrm{F}, \mathrm{mc}}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\eta_{\mathrm{F}, \mathrm{mc}}+1} \\ \times e^{-\left[a_{1, \mathrm{mc}} m_1+\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}\right] \frac{\gamma}{\bar{\gamma}_1}} K_{\tau_{\mathrm{mc}}}\left(\alpha_{\mathrm{F}, \mathrm{mc}} \frac{\gamma}{\bar{\gamma}_1}\right) \end{gathered}$$where
(21)[TeX:] $$\begin{aligned} & \Xi_{\mathrm{F}, \mathrm{mc}}=\Delta_{1, \mathrm{mc}} \nabla_{2, \mathrm{mc}} m_1 b_{1, \mathrm{mc}} \\ & \quad \times\left(\frac{m_2}{\sigma}\right)^{\eta_{2, \mathrm{mc}}}\left[\frac{a_{1, \mathrm{mc}} m_1}{\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}}\right]^{\frac{\tau \mathrm{mc}}{2}} \end{aligned}$$and [TeX:] $$K_v(\cdot)$$ is the modified Bessel function of the second kind with ν-th order[37], [TeX:] $$\alpha_{\mathrm{F}, \mathrm{mc}}= 2 \sqrt{\frac{a_{1, \mathrm{mc}}\left(c_{2, \mathrm{mc}}+1\right) m_1 m_2}{\sigma}}$$, [TeX:] $$\eta \mathrm{F}_{, \mathrm{mc}}=b_{1, \mathrm{mc}}+\eta_{2, \mathrm{mc}}-1$$, [TeX:] $$\tau_{\mathrm{mc}}=\eta_{2, \mathrm{mc}}-k$$ and [TeX:] $$\bar{\gamma}_2=\sigma \bar{\gamma}_1$$. Also, PDF of the received SNR for the triple selection with MRC is given by differentiating Eq.(16)
(22)[TeX:] $$\begin{aligned} f_{\mathrm{t}, \mathrm{mc}}(\gamma) & =\frac{d F_{\mathrm{t}, \mathrm{mc}}(\gamma)}{d \gamma} \\ = & f_{2, \mathrm{mc}}(\gamma)-F_{1, \mathrm{mc}}(\infty) f_{2, \mathrm{mc}}(\gamma) \\ + & \int_\gamma^{\infty} \frac{x^2}{(x-\gamma)^2} f_{1, \mathrm{mc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{mc}}(x) d x \\ = & \int_\gamma^{\infty} \frac{x^2}{(x-\gamma)^2} f_{1, \mathrm{mc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{mc}}(x) d x \end{aligned}$$where f1, mc(γ) with D=R, M=NA, N=NR, s=1 presents PDF for the transmit antenna and relay node selection with MRC in source-relay link. By substituting Eq.(12) into Eq.(22), PDF of the received SNR for the triple selection with MRC is given by
(23)[TeX:] $$\begin{aligned} & f_{\mathrm{t}, \mathrm{mc}}(\gamma)=\int_\gamma^{\infty} \frac{x^2}{(x-\gamma)^2} f_{1, \mathrm{mc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{mc}}(x) d x \\ = & \sum_{\mathrm{f}, \mathrm{mc}} \nabla_{1, \mathrm{mc}} \nabla_{2, \mathrm{mc}}\left(\frac{m_1}{\bar{\gamma}_1}\right)\left(\frac{m_2}{\bar{\gamma}_2}\right) \\ \times & \int_\gamma^{\infty} \frac{x^2}{(x-\gamma)^2}\left(\frac{m_1}{\bar{\gamma}_1} \frac{x \gamma}{x-\gamma}\right)^{\eta_{1, \mathrm{mc}}-1} e^{-\left(c_{1, \mathrm{mc}}+1\right) \frac{m_1}{\bar{\gamma}_1} \frac{x \gamma}{x-\gamma}} \\ \times & \left(m_2 \frac{x}{\bar{\gamma}_2}\right)^{\eta_{2, \mathrm{mc}}-1} e^{-\left(c_{2, \mathrm{mc}}+1\right) m_2 \frac{x}{\bar{\gamma}_2}} d x \end{aligned}$$where
(24)[TeX:] $$\sum_{\mathrm{f}, \mathrm{mc}}=\sum_{I_{1, \mathrm{RN}_{\mathrm{A}}-1}} \sum_{P_{1, \mathrm{RN}_{\mathrm{A}}-1}} \sum_{I_{2, \mathrm{UN}_{\mathrm{R}}-1}} \sum_{P_{2, \mathrm{UN}_{\mathrm{R}}-1}} .$$Using binomial expansion and integral function[37], Eq.(3.471.9), the exact closed-form PDF expression for the triple selection with MRC is obtained by
(25)[TeX:] $$\begin{aligned} & f_{\mathrm{t}, \mathrm{mc}}(\gamma)=2 \sum_{\mathrm{f}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{mc}}}\binom{\eta_{\mathrm{f}, \mathrm{mc}}}{k} \Xi_{\mathrm{f}, \mathrm{mc}} \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\eta_{\mathrm{f}, \mathrm{mc}}-1} \\ & \times e^{-\left[\left(c_{1, \mathrm{mc}}+1\right) m_1+\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}\right] \frac{\gamma}{\bar{\gamma}_1}} K_{\tau_{\mathrm{mc}}}\left(\alpha_{\mathrm{f}, \mathrm{mc}} \frac{\gamma}{\bar{\gamma}_1}\right) \end{aligned}$$where [TeX:] $$\Xi_{\mathrm{f}, \mathrm{mc}}=\nabla_{1, \mathrm{mc}} \nabla_{2, \mathrm{mc}} m_1 \eta_{1, \mathrm{mc}}\left(\frac{m_2}{\sigma}\right)^{\eta_{2, \mathrm{mc}}}\left[\frac{\left(c_{1, \mathrm{mc}}+1\right) m_1}{\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}}\right]^{\frac{\tau_{\mathrm{mc}}}{2}}$$ and [TeX:] $$\alpha_{\mathrm{f}, \mathrm{mc}}=2 \sqrt{\frac{\left(c_{1, \mathrm{mc}}+1\right)\left(c_{2, \mathrm{mc}}+1\right) m_1 m_2}{\sigma}}$$ and [TeX:] $$\eta_{\mathrm{f}, \mathrm{mc}}=\eta_{1, \mathrm{mc}} + \eta_{2,\mathrm{mc}}$$. 3.1.2 SC Similarly to above MRC, PDF and CDF of the re-ceived SNR for the transmit antenna and node se-lection with SC can be derived by using Eq.(3) and Eq.(4)
(27)[TeX:] $$F_{\mathrm{s}, \mathrm{sc}}(\gamma)=\left[F_{\mathrm{sc}}(\gamma)\right]^{\mathrm{DMN}}$$and
(28)[TeX:] $$f_{\mathrm{s}, \mathrm{sc}}(\gamma)=\mathrm{DMN}\left[F_{\mathrm{sc}}(\gamma)\right]^{\mathrm{DMN}-1} f_{\mathrm{sc}}(\gamma) .$$Using binomial expansion, CDF of the received SNR for the node and transmit antenna selection with SC can be obtained by substituting Eq.(3) into Eq.(27)
(29)[TeX:] $$F_{\mathrm{s}, \mathrm{sc}}(\gamma)=\sum_{P_{\mathrm{s}, \mathrm{DMN}}} \sum_{I_{\mathrm{s}}, \mathrm{DMN}} \triangle_{\mathrm{s}, \mathrm{sc}}\left(m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{b_{\mathrm{s}, \mathrm{sc}}} e^{-a_{\mathrm{s}, \mathrm{sc}} m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}}$$where [TeX:] $$a_{\mathrm{s}, \mathrm{sc}}=\sum_{j=1}^{\mathrm{DMN}} p_{\mathrm{s}, j},$$, [TeX:] $$b_{\mathrm{s}, \mathrm{sc}}=\sum_{j=1}^{\mathrm{DMN}} i_{\mathrm{s}, j} \cdot \sum_{P_{\mathrm{DMN}}}$$ and [TeX:] $$\sum_{I_{\mathrm{DMN}}}$$ denote (DMN)-fold summations given by
(30)[TeX:] $$\sum_{P_{\mathrm{s}, \mathrm{DMN}}}=\sum_{p_{\mathrm{s}, 1}=0}^1 \ldots \sum_{p_{\mathrm{s}, \mathrm{DMN}}=0}^1$$
(31)[TeX:] $$\sum_{I_{\mathrm{s}, \mathrm{DMN}}}=\sum_{i_{\mathrm{s}, 1}=0}^{p_{\mathrm{s}, 1}\left(m_{\mathrm{s}}-1\right)} \cdots \sum_{i_{\mathrm{s}, \mathrm{DMN}}=0}^{p_{\mathrm{s}, \mathrm{DMN}}\left(m_{\mathrm{s}}-1\right)}$$and
(32)[TeX:] $$\triangle_{\mathrm{s}, \mathrm{sc}}=\frac{(-1)^{a_{\mathrm{s}, \mathrm{sc}}}}{\prod_{j=1}^{\mathrm{DMM}}\left(i_{\mathrm{s}, j}\right)!}$$where s = 1 for the source-relay link and s = 2 for the relay user link. Similarly, PDF is given by substituting Eq.(3) and Eq.(4) into Eq.(28)
(33)[TeX:] $$\begin{aligned} f_{\mathrm{s}, \mathrm{sc}}(\gamma) & =\sum_{P_{\mathrm{s}, \mathrm{DMN}-1} I_{\mathrm{s}, \mathrm{DMN}-1}} \nabla_{\mathrm{s}, \mathrm{sc}}\left(\frac{m_{\mathrm{s}}}{\bar{\gamma}_{\mathrm{s}}}\right) \\ & \times\left(m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{\eta_{\mathrm{s}, \mathrm{sc}}-1} e^{-\left(c_{\mathrm{s}, \mathrm{sc}}+1\right) m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}} \end{aligned}$$where [TeX:] $$\eta_{\mathrm{s}, \mathrm{sc}}=d_{\mathrm{s}, \mathrm{sc}}+m_{\mathrm{s}}$$ and [TeX:] $$c_{\mathrm{s}, \mathrm{sc}}=\sum_{j=1}^{\mathrm{DMN}-1} p_{\mathrm{s}, j}$$, [TeX:] $$\sum_{j=1}^{\mathrm{DMN}-1} i_{\mathrm{s}, j} \cdot \sum_{P_{\mathrm{DMN}-1}}$$ and [TeX:] $$\sum_{I_{\mathrm{DMN}-1}}$$ denote (DMN − 1)-fold summations given by
(34)[TeX:] $$\sum_{P_{\mathrm{s}, \mathrm{DMN}-1}}=\sum_{p_{\mathrm{s}, 1}=0}^1 \ldots \sum_{p_{\mathrm{s}, \mathrm{DMN}-1}=0}^1,$$
(35)[TeX:] $$\sum_{I_{\mathrm{s}, \mathrm{DMN}-1}}=\sum_{i_{\mathrm{s}, 1}=0}^{p_{\mathrm{s}, 1}\left(m_{\mathrm{s}}-1\right)} \cdots \sum_{i_{\mathrm{s}, \mathrm{DMN}}=0}^{p_{\mathrm{s}, \mathrm{DMN}-1}\left(m_{\mathrm{s}}-1\right)},$$and
(36)[TeX:] $$\nabla_{\mathrm{s}, \mathrm{sc}}=\mathrm{DMN} \frac{(-1)^{c_{\mathrm{s}, \mathrm{sc}}}}{\prod_{j=1}^{\mathrm{DMN}-1}\left(i_{\mathrm{s}, j}\right)!\left(m_{\mathrm{s}}-1\right)!}$$Since Eq.(29) can be rewritten by
(37)[TeX:] $$F_{\mathrm{s}, \mathrm{sc}}(\gamma)=1+\sum_{p_{\mathrm{s}, j} \notin \text { all zero } I_{\mathrm{s}, \mathrm{DMN}}} \triangle_{\mathrm{s}, \mathrm{sc}}\left(m_{\mathrm{s}} \frac{\gamma}{\bar{\gamma}_{\mathrm{s}}}\right)^{b_{\mathrm{s}, \mathrm{sc}}} e^{-a_{\mathrm{s}, \mathrm{sc}} m_{\mathrm{s}} \frac{\gamma}{\bar\gamma_{\mathrm{s}}}},$$CDF of the received SNR for the triple selection with SC is obtained by substituting Eq.(33) and Eq.(37) into Eq.(16)
(38)[TeX:] $$\begin{aligned} & F_{\mathrm{t}, \mathrm{sc}}(\gamma)=1+\int_\gamma^{\infty} F_{1, \mathrm{sc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{sc}}(x) d x \\ = & 1+\sum_{\mathrm{F}, \mathrm{sc}} \triangle_{1, \mathrm{sc}} \nabla_{2, \mathrm{sc}}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{b_{1, \mathrm{sc}}}\left(\frac{\gamma}{\bar{\gamma}_2}\right)^{\eta_{2, \mathrm{sc}}} \\ \times & \int_0^{\infty}\left(\frac{\gamma(\gamma+z)}{z}\right)^{b_{1, \mathrm{sc}}}(\gamma+z)^{\eta_{2, \mathrm{sc}}-1} \\ \times & e^{-a_{1, \mathrm{sc}} \frac{m_1}{\bar{\gamma}_1} \frac{\gamma(\gamma+z)}{z}} e^{-\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\bar{\gamma}_2}(\gamma+z)} d z \end{aligned}$$where
(39)[TeX:] $$\sum_{\mathrm{F}, \mathrm{sc}}=\sum_{p_{1, j} \notin \text { all }} \sum_{\text {zero } I_{1, \mathrm{RN}_{\mathrm{A}} \mathrm{~N}_{\mathrm{R}}}} \sum_{P_{2, \mathrm{UN}_{\mathrm{R}} \mathrm{~N}_{\mathrm{B}}-1}} \sum_{I_{2, \mathrm{UN}_{\mathrm{R}} \mathrm{~N}_{\mathrm{B}}-1}} .$$and [TeX:] $$F_{1, \mathrm{sc}}(\gamma)$$ with D = R, M = NA, N = NR, s = 1 presents CDF for the transmit antenna and relay node selection with SC in source-relay link. [TeX:] $$f_{2, \mathrm{sc}}(\gamma)$$ with D=B, M=NR, N=NB, s=2 presents PDF for the transmit antenna and user node selection with SC in relay-user link. Using binomial expansion, the exact closed-form CDF expression for the triple selection with SC is given
(40)[TeX:] $$\begin{aligned} F_{\mathrm{t}, \mathrm{sc}}(\gamma) & =1+2 \sum_{\mathrm{F}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{sc}}}\binom{\eta_{\mathrm{F}, \mathrm{sc}}}{k} \Xi_{\mathrm{F}, \mathrm{sc}}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{b_{1, \mathrm{sc}}+\eta_{2, \mathrm{sc}}} \\ & \times e^{-\left[a_{1, \mathrm{sc}} m_1+\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}\right] \frac{\gamma}{\bar{\gamma}_1}} K_{\tau_{\mathrm{sc}}}\left(\alpha_{\mathrm{F}, \mathrm{sc}} \frac{\gamma}{\bar{\gamma}_1}\right) \end{aligned}$$where
(41)[TeX:] $$\Xi_{\mathrm{F}, \mathrm{sc}}=\triangle_{1, \mathrm{sc}} \nabla_{2, \mathrm{sc}} m_1{ }^{b_{1, \mathrm{sc}}}\left(\frac{m_2}{\sigma}\right)^{\eta_{2, \mathrm{sc}}}\left[\frac{a_{1, \mathrm{sc}} m_1}{\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}}\right]^{\frac{\tau_{\mathrm{sc}}}{2}}$$and [TeX:] $$\alpha_{\mathrm{F}, \mathrm{sc}}=2 \sqrt{\frac{a_{1, \mathrm{sc}}\left(c_{2, \mathrm{sc}}+1\right) m_1 m_2}{\sigma}}$$, [TeX:] $$\eta_{\mathrm{F}, \mathrm{sc}}=b_{1, \mathrm{sc}}+\eta_{2, \mathrm{sc}}-1$$, [TeX:] $$\tau_{\mathrm{sc}}=\eta_{2, \mathrm{sc}}-k$$. Using binomial expansion, the exact closed-form PDF expression for the triple selection with SC is given by substituting Eq.(33) into Eq.(22)
(42)[TeX:] $$\begin{aligned} & f_{\mathrm{t}, \mathrm{sc}}(\gamma)=\int_\gamma^{\infty} \frac{x^2}{(x-\gamma)^2} f_{1, \mathrm{sc}}\left(\frac{x \gamma}{x-\gamma}\right) f_{2, \mathrm{sc}}(x) d x \\ & \quad=2 \sum_{\mathrm{f}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{sc}}}\binom{\eta_{\mathrm{f}, \mathrm{sc}}}{k} \Xi_{\mathrm{f}, \mathrm{sc}} \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\eta_{\mathrm{f}, \mathrm{sc}}-1} \\ & \quad \times e^{-\left[\left(c_{1, \mathrm{sc}}+1\right) m_1+\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}\right] \frac{\gamma}{\bar{\gamma}_1}} K_{\tau_{\mathrm{sc}}}\left(\alpha_{\mathrm{f}, \mathrm{sc}} \frac{\gamma}{\bar{\gamma}_1}\right) \end{aligned}$$where
(43)[TeX:] $$\sum_{\mathrm{f}, \mathrm{sc}}=\sum_{I_{1, \mathrm{RN}_{\mathrm{A}} \mathrm{~N}_{\mathrm{R}}-1}} \sum_{P_{1, \mathrm{RN}_{\mathrm{A}} \mathrm{~N}_{\mathrm{R}}-1}} \sum_{I_{2, \mathrm{UN}_{\mathrm{R}} \mathrm{~N}_{\mathrm{B}}-1}} \sum_{P_{2, \mathrm{UN}_{\mathrm{R}} \mathrm{~N}_{\mathrm{B}}-1},},$$
(44)[TeX:] $$\Xi_{\mathrm{f}, \mathrm{sc}}=\nabla_{1, \mathrm{sc}} \nabla_{2, \mathrm{sc}} m_1 \eta_{1, \mathrm{sc}}\left(\frac{m_2}{\sigma}\right)^{\eta_{2, \mathrm{sc}}}\left[\frac{\left(c_{1, \mathrm{sc}}+1\right) m_1}{\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}}\right]^{\frac{\tau_{\mathrm{sc}}}{2}},$$and [TeX:] $$f_{1, \mathrm{sc}}(\gamma)$$ with D=R, M=NA, N=NR, s=1 presents PDF for transmit antenna and relay node selection with SC in source-relay link. [TeX:] $$\alpha_{f,sc} = 2 \sqrt{\frac{\left(c_{1, \mathrm{sc}}+1\right)\left(c_{2, \mathrm{sc}}+1\right) m_1 m_2}{\sigma}}$$ and [TeX:] $$\eta_{\mathrm{f}, \mathrm{sc}}=\eta_{1, \mathrm{sc}}+\eta_{2, \mathrm{sc}}$$. 3.2 Distribution of eavesdropperFrom the eavesdropper point of view, the triple selection of authorized system is equivalent to random selection. Thus, CDF of the received SNR for the eavesdropper with MRC over Nakagami fading channels is given by Eq.(1)
where
(46)[TeX:] $$\Omega_{\mathrm{e}, \mathrm{mc}}=-e^{-m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}} \sum_{i_{\mathrm{e}}=0}^{m_{\mathrm{e}} \mathrm{~N}_{\mathrm{E}}-1} \frac{\left(m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} .$$Using binomial expansion, Eq.(45) can be represented by
(47)[TeX:] $$F_{\mathrm{e}, \mathrm{mc}}(\gamma)=\sum_{p_{\mathrm{e}}=0}^1 \sum_{i_{\mathrm{e}}=0}^{p_{\mathrm{e}}\left(m_{\mathrm{e}} \mathrm{~N}_{\mathrm{E}}-1\right)}(-1)^{p_{\mathrm{e}}} e^{-p_{\mathrm{e}} m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}} \frac{\left(m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} .$$Similarly, using binomial expansion, CDF of the received SNR for eavesdropper with SC can be obtained by Eq.(3)
(48)[TeX:] $$\begin{aligned} & F_{\mathrm{e}, \mathrm{sc}}(\gamma)=\left[F_{\mathrm{sc}}(\gamma)\right]^{\mathrm{N}_{\mathrm{E}}} \\ & \quad=\sum_{P_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}} \sum_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}} \triangle_{\mathrm{e}}\left(m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} e^{-a_{\mathrm{e}} m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}} \end{aligned}$$where [TeX:] $$a_{\mathrm{e}}=\sum_{j=1}^{\mathrm{N}_{\mathrm{E}}} p_{\mathrm{e}, j}$$,[TeX:] $$b_{\mathrm{e}}=\sum_{j=1}^{\mathrm{N}_{\mathrm{E}}} i_{\mathrm{e}, j} \cdot \sum_{P_{\mathrm{N}_{\mathrm{E}}}}$$ and [TeX:] $$\sum_{I_{\mathrm{N}_{\mathrm{E}}}}$$ denote (NE)-fold summations given by
(49)[TeX:] $$\sum_{P_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}}=\sum_{p_{\mathrm{e}, 1}=0}^1 \cdots \sum_{p_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}=0}^1$$
(50)[TeX:] $$\sum_{I_{\mathrm{e}, N_{\mathrm{E}}}}=\sum_{i_{\mathrm{e}, 1}=0}^{p_{\mathrm{e}, 1}\left(m_{\mathrm{e}}-1\right)} \cdots \sum_{i_{\mathrm{e}, N_{\mathrm{E}}}=0}^{p_{\mathrm{e}, N_{\mathrm{E}}}\left(m_{\mathrm{e}}-1\right)},$$and
(51)[TeX:] $$\Delta_{\mathrm{e}}=\frac{(-1)^{a_{\mathrm{e}}}}{\prod_{j=1}^{\mathrm{N}_{\mathrm{E}}}\left(i_{\mathrm{e}, j}\right)!}$$Further, Eq.(48) can be rewritten by
where
(53)[TeX:] $$\Omega_{\mathrm{e}, \mathrm{sc}}=\sum_{p_{\mathrm{e}, j} \notin \text { all zero }} \sum_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}} \triangle_{\mathrm{e}}\left(m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} e^{-a_{\mathrm{e}} m_{\mathrm{e}} \frac{\gamma}{\bar{\gamma}_{\mathrm{e}}}} .$$3.3 Secrecy rate3.3.1 MRC Similar to the works[11,38], the exact secrecy rate of the MRC-based triple selection is obtained by
(54)[TeX:] $$C_{\mathrm{mc}}(\gamma)=\frac{1}{\ln 2} \int_0^{\infty} \frac{F_{\mathrm{e}, \mathrm{mc}}(\gamma)}{\gamma+1}\left[1-F_{\mathrm{t}, \mathrm{mc}}(\gamma)\right] d \gamma .$$To derive analytical expression for the secrecy rate using Eq.(54), it is necessary to rewrite the modified Bessel function into series form[39] as follows
(55)[TeX:] $$K_\tau\left(\alpha \frac{\gamma}{\bar{\gamma}}\right)=e^{-\alpha \frac{\gamma}{\bar{\gamma}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \xi(|\tau|, r, l)\left(\alpha \frac{\gamma}{\bar{\gamma}}\right)^{l-|\tau|},|\tau|>0$$where [TeX:] $$\xi(|\tau|, r, l)$$ is defined in the work[39] and using even function property[39], Eq.(10.27.3),
(56)[TeX:] $$K_0\left(\alpha \frac{\gamma}{\bar{\gamma}}\right)=K_2\left(\alpha \frac{\gamma}{\bar{\gamma}}\right)-2\left(\frac{\bar{\gamma}}{\alpha \gamma}\right) K_1\left(\alpha \frac{\gamma}{\bar{\gamma}}\right), \tau=0 .$$Using Eq.(55) and Eq.(56), CDF of the received SNR for the triple selection can be rewritten by
(57)[TeX:] $$\begin{aligned} F_{\mathrm{t}, \mathrm{mc}}(\gamma) & =1+2 \sum_{\mathrm{F}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{F}, \mathrm{mc}}}{k} \Xi_{\mathrm{F}, \mathrm{mc}} \\ & \times \lambda_{\mathrm{F}, \mathrm{mc}}(\gamma) e^{-\left(\zeta_{\mathrm{F}, \mathrm{mc}}+\alpha_{\mathrm{F}, \mathrm{mc}}\right) \frac{\gamma}{\bar{\gamma}_1}} \end{aligned}$$where
(58)[TeX:] $$\lambda_{\mathrm{F}, \mathrm{mc}}(\gamma)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{mc}}\right|, r, l\right) \alpha_{\mathrm{F}, \mathrm{mc}}^{l-\left|\tau_{\mathrm{mc}}\right|} \\ \times\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{F}, \mathrm{mc}}}-\left|\tau_{\mathrm{mc}}\right|,\left|\tau_{\mathrm{mc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{F}, \mathrm{mc}}^{l-2} \\ \times\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{F}, \mathrm{mc}}-2}, \tau_{\mathrm{mc}}=0 \end{array}\right.$$and [TeX:] $$\zeta_{\mathrm{F}, \mathrm{mc}}=-\left[a_{1, \mathrm{mc}} m_1+\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}\right]$$, and [TeX:] $$\rho_{F,mc} = b_{1, \mathrm{mc}}+\eta_{2, \mathrm{mc}}+1$$. Similarly, PDF of the received SNR for the triple selection can be also rewritten by
(59)[TeX:] $$\begin{aligned} f_{\mathrm{t}, \mathrm{mc}}(\gamma) & =2 \sum_{\mathrm{f}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{f}, \mathrm{mc}}}{k} \Xi_{\mathrm{f}, \mathrm{mc}} \\ & \times \lambda_{\mathrm{f}, \mathrm{mc}}(\gamma) e^{-\left(\zeta_{\mathrm{f}, \mathrm{mc}}+\alpha_{\mathrm{f}, \mathrm{mc}}\right) \frac{\gamma}{\bar{\gamma}_1}} \end{aligned}$$where
(60)[TeX:] $$\lambda_{\mathrm{f}, \mathrm{mc}}(\gamma)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{mc}}\right|, r, l\right) \alpha_{\mathrm{f}, \mathrm{mc}}^{l-\left|\tau_{\mathrm{mc}}\right|} \\ \times \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{f}, \mathrm{mc}}-\left|\tau_{\mathrm{mc}}\right|-1},\left|\tau_{\mathrm{mc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{f}, \mathrm{mc}}^{l-3} \\ \times \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{f}, \mathrm{mc}}-3}, \tau_{\mathrm{mc}}=0 \end{array}\right.$$and [TeX:] $$\zeta_{\mathrm{f}, \mathrm{mc}}=-\left[\left(c_{1, \mathrm{mc}}+1\right) m_1+\left(c_{2, \mathrm{mc}}+1\right) \frac{m_2}{\sigma}\right]$$, and [TeX:] $$\rho_{\mathrm{f}, \mathrm{mc}} =\eta_{1, \mathrm{mc}}+\eta_{2, \mathrm{mc}}+1$$. By substituting Eq.(47) and Eq.(57) into Eq.(54), the exact secrecy rate expression for the triple selection with MRC over Nakagami fading channel is given by
(61)[TeX:] $$\begin{aligned} & C_{\mathrm{mc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)=\frac{-2}{\ln 2} \sum_{\mathrm{F}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \sum_{p_{\mathrm{e}}=0}^1 \sum_{i_{\mathrm{e}}=0}^{p_{\mathrm{e}}} \\ & \quad \times\binom{\eta_{\mathrm{F}, \mathrm{mc}}}{k} \Xi_{\mathrm{F}, \mathrm{mc}}(-1)^{p_{\mathrm{e}}} \frac{\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} \varpi_{\mathrm{F}, \mathrm{mc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right) \end{aligned}$$where
(62)[TeX:] $$\omega_{\mathrm{F}, \mathrm{mc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{mc}}\right|, r, l\right) \alpha_{\mathrm{F}, \mathrm{mc}}^{l-\left|\tau_{\mathrm{mc}}\right|} \frac{\Gamma\left(\beta_{\mathrm{F}, \mathrm{mc}}^1\right)}{\bar{\gamma}_1^{\rho_{\mathrm{F}, \mathrm{mc}}-\left|\tau_{\mathrm{mc}}\right|}} \\ \times \psi\left(\beta_{\mathrm{F}, \mathrm{mc}}^1, \beta_{\mathrm{F}, \mathrm{mc}}^1, \delta_{\mathrm{F}, \mathrm{mc}}\right),\left|\tau_{\mathrm{mc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{F}, \mathrm{mc}}^{l-2} \frac{\Gamma\left(\beta_{\mathrm{F}, \mathrm{mc}}^2\right)}{\bar{\gamma}^{\rho_{\mathrm{F}, \mathrm{mc}}-2}} \\ \times \Psi\left(\beta_{\mathrm{F}, \mathrm{mc}}^2, \beta_{\mathrm{F}, \mathrm{mc}}^2, \delta_{\mathrm{F}, \mathrm{mc}}\right), \tau_{\mathrm{mc}}=0 \end{array}\right.$$and [TeX:] $$\Psi(\cdot)$$ is the confluent hypergeometric function[37]. [TeX:] $$\beta_{\mathrm{F}, \mathrm{mc}}^1=\rho_{\mathrm{F}, \mathrm{mc}}-\left|\tau_{\mathrm{mc}}\right|+i_{\mathrm{e}}+1$$, [TeX:] $$\beta_{\mathrm{F}, \mathrm{mc}}^2=\rho_{\mathrm{F}, \mathrm{mc}}+i_{\mathrm{e}}-1$$, [TeX:] $$\delta_{\mathrm{F}, \mathrm{mc}}=\left(\zeta_{\mathrm{F}, \mathrm{mc}}+\alpha_{\mathrm{F}, \mathrm{mc}}\right) \frac{1}{\bar{\gamma}_{\mathrm{l}}}+p_{\mathrm{e}} m_{\mathrm{e}} \frac{1}{\bar{\gamma}_{\mathrm{e}}}$$. When [TeX:] $$$$, the asymptotic secrecy rate of the MRC-based triple selection can be approximated by[38]
(63)[TeX:] $$C_{\mathrm{mc}}^{\infty}=\frac{1}{\ln 2} \int_0^{\infty} \ln (\gamma) f_{\mathrm{t}, \mathrm{mc}}(\gamma) d \gamma+\frac{1}{\ln 2} \int_0^{\infty} \frac{\Omega_{\mathrm{e}, \mathrm{mc}}(\gamma)}{1+\gamma} d \gamma .$$The first integral of Eq.(63) can be evaluated by
(64)[TeX:] $$\begin{aligned} & \frac{1}{\ln 2} \int_0^{\infty} \ln (\gamma) f_{\mathrm{t}, \mathrm{mc}}(\gamma) d \gamma=\log _2 \bar{\gamma}_1 \\ & +\frac{2}{\ln 2} \sum_{\mathrm{f}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{f}, \mathrm{mc}}}{k} \Xi_{\mathrm{f}, \mathrm{mc}} \varpi_{\mathrm{f}, \mathrm{mc}}\left(\bar{\gamma}_1\right) \end{aligned}$$where
(65)[TeX:] $$\varpi_{\mathrm{f}, \mathrm{mc}}\left(\bar{\gamma}_1\right)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{mc}}\right|, r, l\right) \alpha_{\mathrm{f}, \mathrm{mc}}^{l-\left|\tau_{\mathrm{mc}}\right|} \frac{\Gamma\left(\beta_{\mathrm{f}, \mathrm{mc}}^1\right)}{\left(\delta_{\mathrm{f}, \mathrm{mc}}\right)^{\beta_{\mathrm{f}, \mathrm{mc}}^1}} \\ \times\left[\psi\left(\beta_{\mathrm{f}, \mathrm{mc}}^1\right)-\ln \left(\delta_{\mathrm{f}, \mathrm{mc}}\right)\right],\left|\tau_{\mathrm{mc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{f}, \mathrm{mc}}^{l-2} \frac{\Gamma\left(\beta_{\mathrm{f}, \mathrm{mc}}^2\right)}{\left(\delta_{\mathrm{f}, \mathrm{mc}}\right)^{\beta_{\mathrm{f}, \mathrm{mc}}^2}} \\ \times\left[\psi\left(\beta_{\mathrm{f}, \mathrm{mc}}^2\right)-\ln \left(\delta_{\mathrm{f}, \mathrm{mc}}\right)\right], \tau_{\mathrm{mc}}=0 \end{array}\right.$$and [TeX:] $$\psi(\cdot)$$ denotes the psi function in Eq.(8.369.1) of the work[37]. [TeX:] $$\beta_{\mathrm{f}, \mathrm{mc}}^1=\rho_{\mathrm{f}, \mathrm{mc}}-\left|\tau_{\mathrm{mc}}\right|$$,[TeX:] $$\beta_{\mathrm{f}, \mathrm{mc}}^2=\rho_{\mathrm{f}, \mathrm{mc}}+i_{\mathrm{e}}-2$$, [TeX:] $$\delta_{\mathrm{f}, \mathrm{mc}}=\left(\zeta_{\mathrm{f}, \mathrm{mc}}+\alpha_{\mathrm{f}, \mathrm{mc}}\right)$$. The second integral of Eq.(63) can be evaluated by
(66)[TeX:] $$\begin{aligned} & \frac{1}{\ln 2} \int_0^{\infty} \frac{\Omega_{\mathrm{e}, \mathrm{mc}}(\gamma)}{1+} d \gamma=-\frac{1}{\ln 2} \sum_{i_{\mathrm{e}}=0}^{m_{\mathrm{e}} \mathrm{~N}_{\mathrm{E}}-1} \frac{\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} \\ & \times \Gamma\left(i_{\mathrm{e}}+1\right) \Psi\left(i_{\mathrm{e}}+1, i_{\mathrm{e}}+1, \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{aligned}$$Thus, the asymptotic secrecy rate expression of the MRC-based triple selection is derived by
(67)[TeX:] $$\begin{aligned} C_{\mathrm{mc}}^{\infty}= & \log _2 \bar{\gamma}_1+\frac{2}{\ln 2} \sum_{\mathrm{f}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \\ & \times\binom{\eta_{\mathrm{f}, \mathrm{mc}}}{k} \Xi_{\mathrm{f}, \mathrm{mc}} \varpi_{\mathrm{f}, \mathrm{mc}}\left(\bar{\gamma}_1\right)-\frac{1}{\ln 2} \sum_{i_{\mathrm{e}}=0}^{m_{\mathrm{e}} \mathrm{~N}_{\mathrm{E}}-1} \frac{\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} \\ & \times \Gamma\left(i_{\mathrm{e}}+1\right) \Psi\left(i_{\mathrm{e}}+1, i_{\mathrm{e}}+1, \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{aligned}$$3.3.2 SC Similar to MRC, the exact secrecy rate of the triple selection with SC is obtained by
(68)[TeX:] $$C_{\mathrm{sc}}(\gamma)=\frac{1}{\ln 2} \int_0^{\infty} \frac{F_{\mathrm{e}, \mathrm{sc}}(\gamma)}{\gamma+1}\left[1-F_{\mathrm{t}, \mathrm{sc}}(\gamma)\right] d \gamma .$$Using Eq.(55) and Eq.(56), CDF of the received SNR for the SC-based triple selection can be rewritten by
(69)[TeX:] $$\begin{aligned} F_{\mathrm{t}, \mathrm{sc}}(\gamma)= & 1+2 \sum_{\mathrm{F}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{sc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{F}, \mathrm{sc}}}{k} \Xi_{\mathrm{F}, \mathrm{sc}} \\ & \times \lambda_{\mathrm{F}, \mathrm{sc}}(\gamma) e^{-\left(\zeta_{\mathrm{F}, \mathrm{sc}}+\alpha_{\mathrm{F}, \mathrm{sc}}\right) \frac{\gamma}{\bar{\gamma}_1}} \end{aligned}$$where
(70)[TeX:] $$\lambda_{\mathrm{F}, \mathrm{sc}}(\gamma)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{sc}}\right|, r, l\right) \alpha_{\mathrm{F}, \mathrm{sc}}^{l-\left|\tau_{\mathrm{sc}}\right|} \\ \times\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{F}, \mathrm{sc}}-\left|\tau_{\mathrm{sc}}\right|},\left|\tau_{\mathrm{sc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{F}, \mathrm{sc}}^{l-2} \\ \times\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{F}, \mathrm{sc}}-2}, \tau_{\mathrm{sc}}=0 \end{array}\right.$$and [TeX:] $$\zeta_{\mathrm{F}, \mathrm{sc}}=-\left[a_{1, \mathrm{sc}} m_1+\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}\right]$$, and [TeX:] $$\rho_{F, s c}=b_{1, \mathrm{sc}}+\eta_{2, \mathrm{sc}}+1$$. Using alternative expression of Bessel function, PDF of the received SNR for the triple selection with SC can be rewritten by
(71)[TeX:] $$\begin{aligned} f_{\mathrm{t}, \mathrm{sc}}(\gamma)= & 2 \sum_{\mathrm{f}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{sc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{f}, \mathrm{sc}}}{k} \Xi_{\mathrm{f}, \mathrm{sc}} \\ & \times \lambda_{\mathrm{f}, \mathrm{sc}}(\gamma) e^{-\left(\zeta_{\mathrm{f}, \mathrm{sc}}+\alpha_{\mathrm{f}, \mathrm{sc}}\right) \frac{\gamma}{\bar{\gamma}_1}} \end{aligned}$$where
(72)[TeX:] $$\lambda_{\mathrm{f}, \mathrm{sc}}(\gamma)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{sc}}\right|, r, l\right) \alpha_{\mathrm{f}, \mathrm{sc}}^{l-\left|\tau_{\mathrm{sc}}\right|} \\ \times \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{f}, \mathrm{sc}}-\left|\tau_{\mathrm{sc}}\right|-1},\left|\tau_{\mathrm{sc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{f}, \mathrm{sc}}^{l-3} \\ \times \frac{1}{\bar{\gamma}_1}\left(\frac{\gamma}{\bar{\gamma}_1}\right)^{\rho_{\mathrm{f}, \mathrm{sc}}-3}, \tau_{\mathrm{sc}}=0 \end{array}\right.$$and [TeX:] $$\zeta_{\mathrm{f}, \mathrm{sc}}=-\left[\left(c_{1, \mathrm{sc}}+1\right) m_1+\left(c_{2, \mathrm{sc}}+1\right) \frac{m_2}{\sigma}\right]$$, and [TeX:] $$\rho_{\mathrm{f}, \mathrm{sc}}=\eta_{1, \mathrm{sc}}+\eta_{2, \mathrm{sc}}+1$$. By substituting Eq.(52) and Eq.(69) into Eq.(68), the exact secrecy rate expression for the triple selection with SC over Nakagami fading channels is given by
(73)[TeX:] $$\begin{aligned} & C_{\mathrm{sc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)=\frac{-2}{\ln 2} \sum_{\mathrm{F}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{F}, \mathrm{sc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \sum_{P_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}} \sum_{I_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}}} \\ & \quad \times\binom{\eta_{\mathrm{F}, \mathrm{sc}}}{k} \Xi_{\mathrm{F}, \mathrm{sc}} \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \varpi_{\mathrm{F}, \mathrm{sc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right) \end{aligned}$$where
(74)[TeX:] $${ }^{\prime} \omega_{\mathrm{F}, \mathrm{sc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{sc}}\right|, r, l\right) \alpha_{\mathrm{F}, \mathrm{sc}}^{l-\left|\tau_{\mathrm{sc}}\right|} \frac{\Gamma\left(\beta_{\mathrm{F}, \mathrm{sc}}^1\right)}{\bar{\gamma}_1^{\rho_{\mathrm{F}, \mathrm{sc}}-\left|\tau_{\mathrm{sc}}\right|}} \\ \times \psi\left(\beta_{\mathrm{F}, \mathrm{sc}}^1, \beta_{\mathrm{F}, \mathrm{sc}}^1, \delta_{\mathrm{F}, \mathrm{sc}}\right),\left|\tau_{\mathrm{sc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{F}, \mathrm{sc}}^{l-2} \frac{\Gamma\left(\beta_{\mathrm{F}, \mathrm{sc}}^2\right)}{\bar{\gamma}^{\rho_{\mathrm{F}, \mathrm{sc}}-2}} \\ \times \Psi\left(\beta_{\mathrm{F}, \mathrm{sc}}^2, \beta_{\mathrm{F}, \mathrm{sc}}^2, \delta_{\mathrm{F}, \mathrm{sc}}\right), \tau_{\mathrm{sc}}=0 \end{array}\right.$$and [TeX:] $$\beta_{\mathrm{F}, \mathrm{sc}}^1=\rho_{\mathrm{F}, \mathrm{sc}}-\left|\tau_{\mathrm{sc}}\right|+b_{\mathrm{e}}+1, \beta_{\mathrm{F}, \mathrm{sc}}^2=\rho_{\mathrm{F}, \mathrm{sc}}+b_{\mathrm{e}}-1$$, [TeX:] $$\delta_{\mathrm{F}, \mathrm{sc}}=\left(\zeta_{\mathrm{F}, \mathrm{sc}}+\alpha_{\mathrm{F}, \mathrm{sc}}\right) \frac{1}{\bar{\gamma}_1}+a_{\mathrm{e}} m_{\mathrm{e}} \frac{1}{\bar{\gamma}_{\mathrm{e}}}$$. When [TeX:] $$\bar{\gamma}_1 \rightarrow \infty,$$, the asymptotic secrecy rate of the SC-based triple selection can be approximated by
(75)[TeX:] $$C_{\mathrm{sc}}^{\infty}=\frac{1}{\ln 2} \int_0^{\infty} \ln (\gamma) f_{\mathrm{t}, \mathrm{sc}}(\gamma) d \gamma+\frac{1}{\ln 2} \int_0^{\infty} \frac{\Omega_{\mathrm{e}, \mathrm{sc}}(\gamma)}{1+\gamma} d \gamma .$$The first integral of Eq.(75) can be evaluated by
(76)[TeX:] $$\begin{aligned} & \frac{1}{\ln 2} \int_0^{\infty} \ln (\gamma) f_{\mathrm{t}, \mathrm{sc}}(\gamma) d \gamma=\log _2 \bar{\gamma}_{\mathrm{l}} \\ & \quad+\frac{2}{\ln 2} \sum_{\mathrm{f}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{sc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{f}, \mathrm{sc}}}{k} \Xi_{\mathrm{f}, \mathrm{sc}} \varpi_{\mathrm{f}, \mathrm{sc}}\left(\bar{\gamma}_1\right) \end{aligned}$$where
(77)[TeX:] $$\omega_{\mathrm{f}, \mathrm{sc}}\left(\bar{\gamma}_1\right)=\left\{\begin{array}{l} \xi\left(\left|\tau_{\mathrm{sc}}\right|, r, l\right) \alpha_{\mathrm{f}, \mathrm{sc}}^{l-\left|\tau_{\mathrm{sc}}\right|} \frac{\Gamma\left(\beta_{\mathrm{f}, \mathrm{sc}}^1\right)}{\left(\delta_{\mathrm{f}, \mathrm{sc}}\right)^{\beta_{\mathrm{t}, \mathrm{sc}}}} \\ \times\left[\psi\left(\beta_{\mathrm{f}, \mathrm{sc}}^1\right)-\ln \left(\delta_{\mathrm{f}, \mathrm{sc}}\right)\right],\left|\tau_{\mathrm{sc}}\right|>0 \\ (\xi(2, r, l)-2 \xi(1, r, l)) \alpha_{\mathrm{f}, \mathrm{sc}}^{l-2} \frac{\Gamma\left(\beta_{\mathrm{f}, \mathrm{sc}}^2\right)}{\left(\delta_{\mathrm{f}, \mathrm{sc}}\right)^{\beta_{\mathrm{f}, \mathrm{sc}}^2}} \\ \times\left[\psi\left(\beta_{\mathrm{f}, \mathrm{sc}}^2\right)-\ln \left(\delta_{\mathrm{f}, \mathrm{sc}}\right)\right], \tau_{\mathrm{sc}}=0 \end{array}\right.$$and [TeX:] $$\beta_{\mathrm{f}, \mathrm{sc}}^1=\rho_{\mathrm{f}, \mathrm{sc}}-\left|\tau_{\mathrm{sc}}\right|$$, [TeX:] $$\beta_{\mathrm{f}, \mathrm{sc}}^2=\rho_{\mathrm{f}, \mathrm{sc}}+b_{\mathrm{e}}-2$$, [TeX:] $$\delta_{\mathrm{f}, \mathrm{sc}}=\left(\zeta_{\mathrm{f}, \mathrm{sc}}+\alpha_{\mathrm{f}, \mathrm{sc}}\right)$$. The second integral of Eq.(75) can be evaluated by
(78)[TeX:] $$\begin{gathered} \frac{1}{\ln 2} \int_0^{\infty} \frac{\Omega_{\mathrm{e}, \mathrm{sc}}(\gamma)}{1+\gamma} d \gamma=\frac{1}{\ln 2} \sum_{p_{\mathrm{e}, j} \notin \text { all zero } I_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}} \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \\ \times \Gamma\left(b_{\mathrm{e}}+1\right) \Psi\left(b_{\mathrm{e}}+1, b_{\mathrm{e}}+1, a_{\mathrm{e}} \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{gathered}$$Thus, the asymptotic secrecy rate expression of the SC-based triple selection is derived by
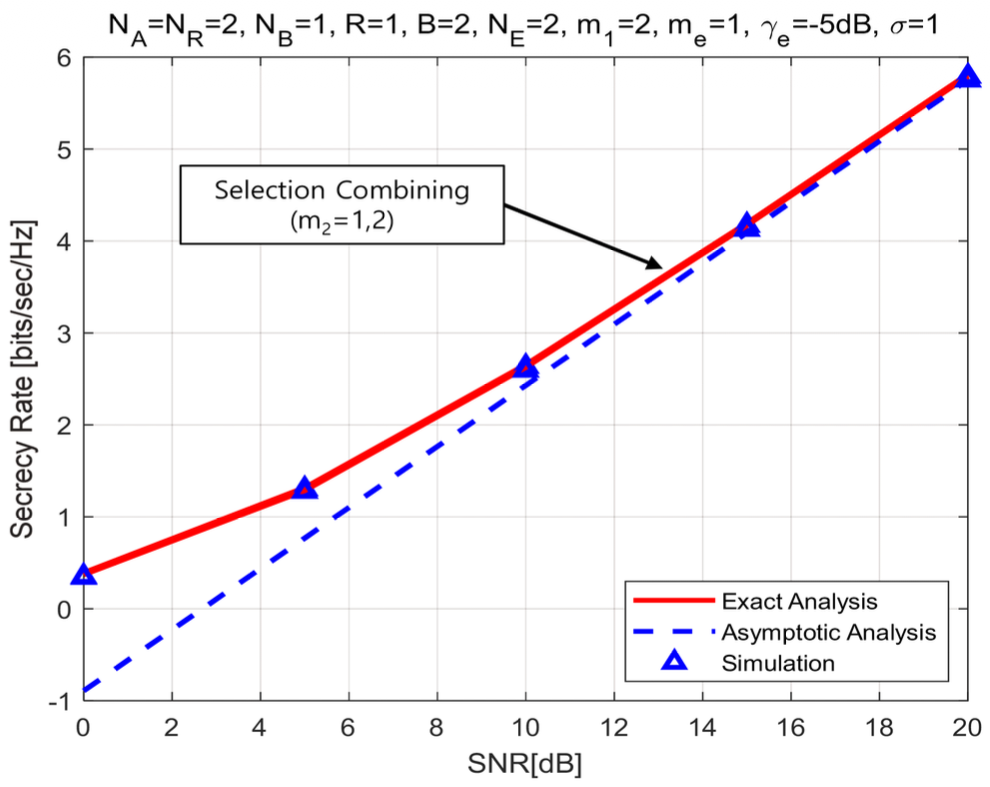
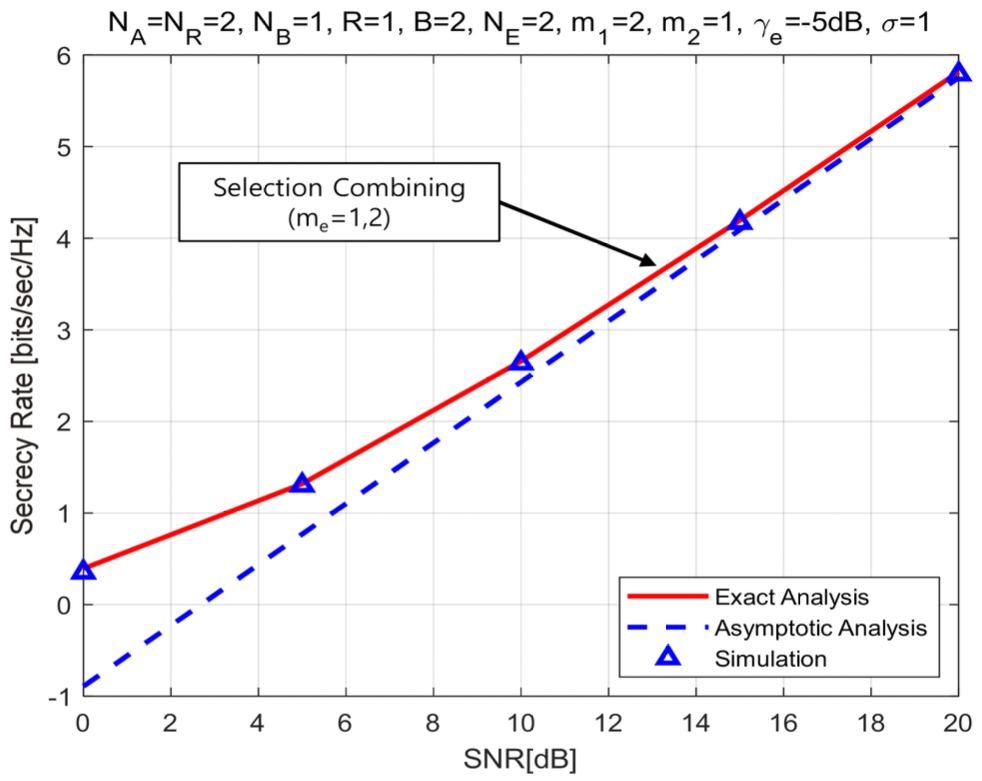
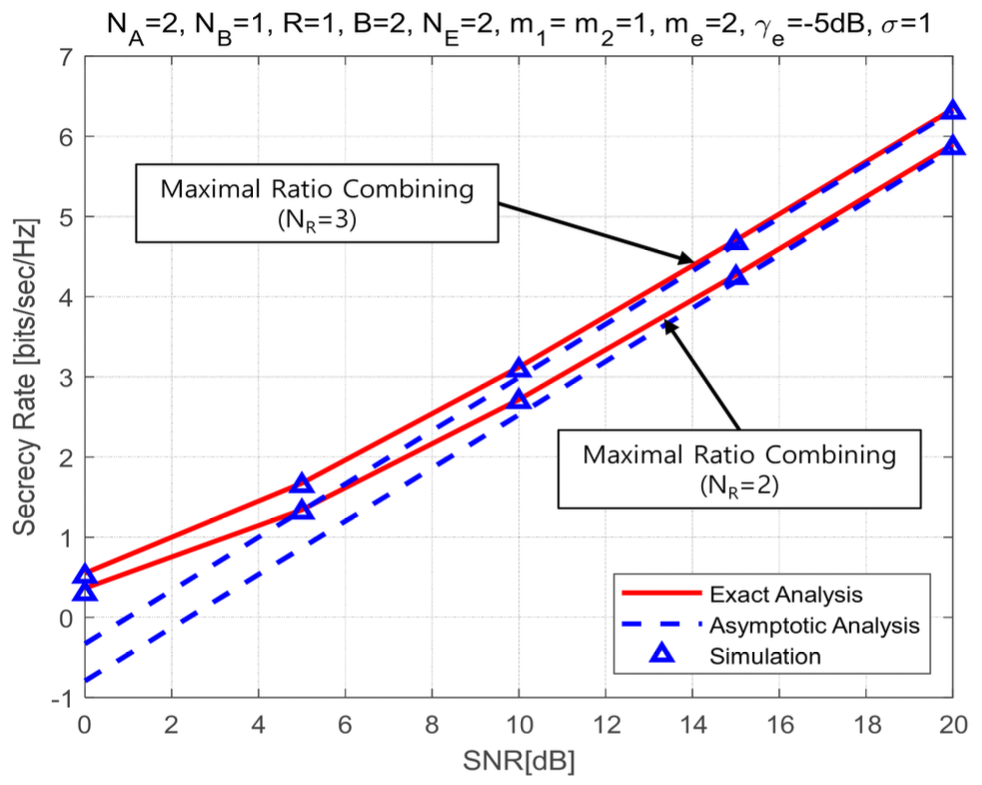
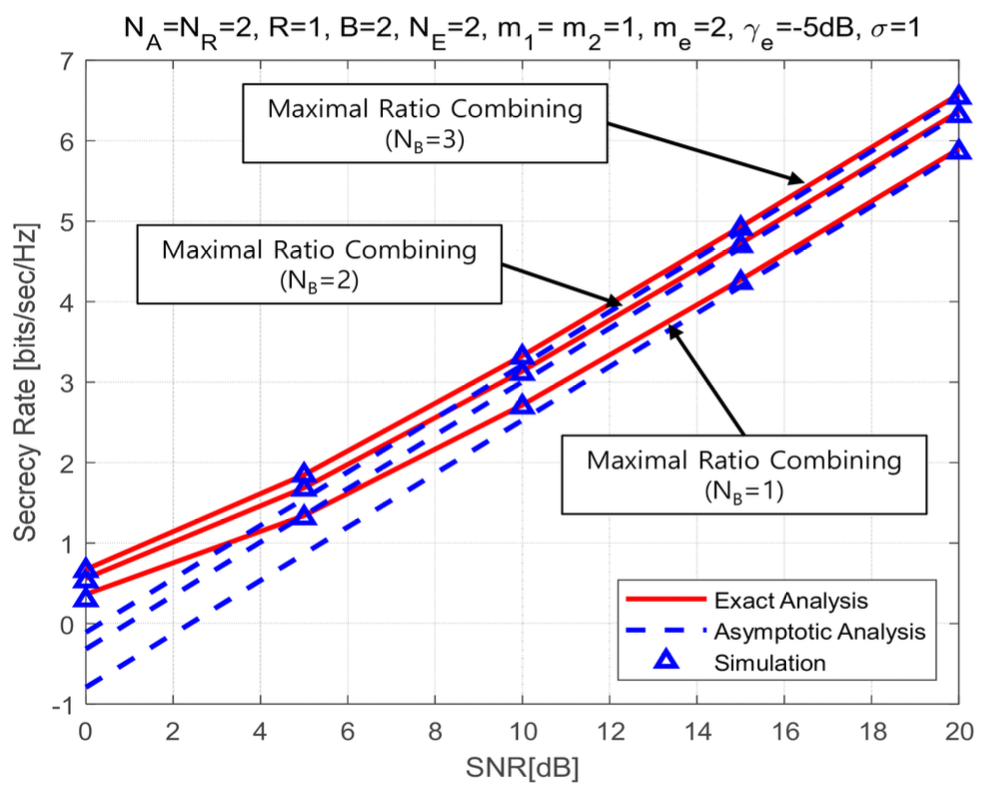
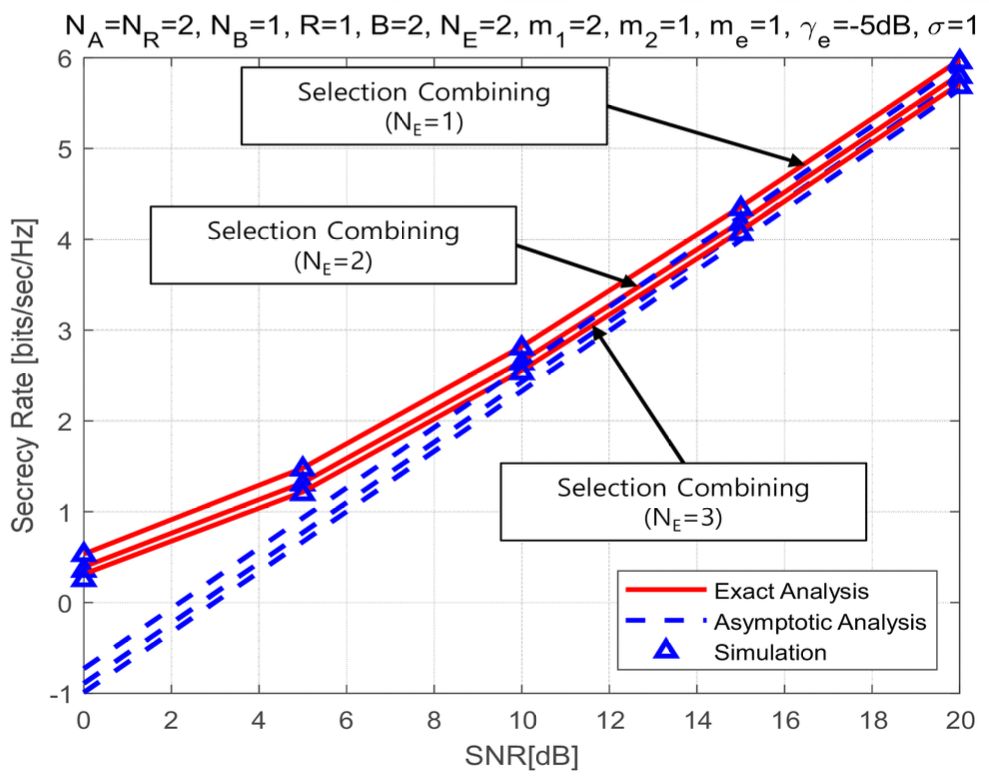
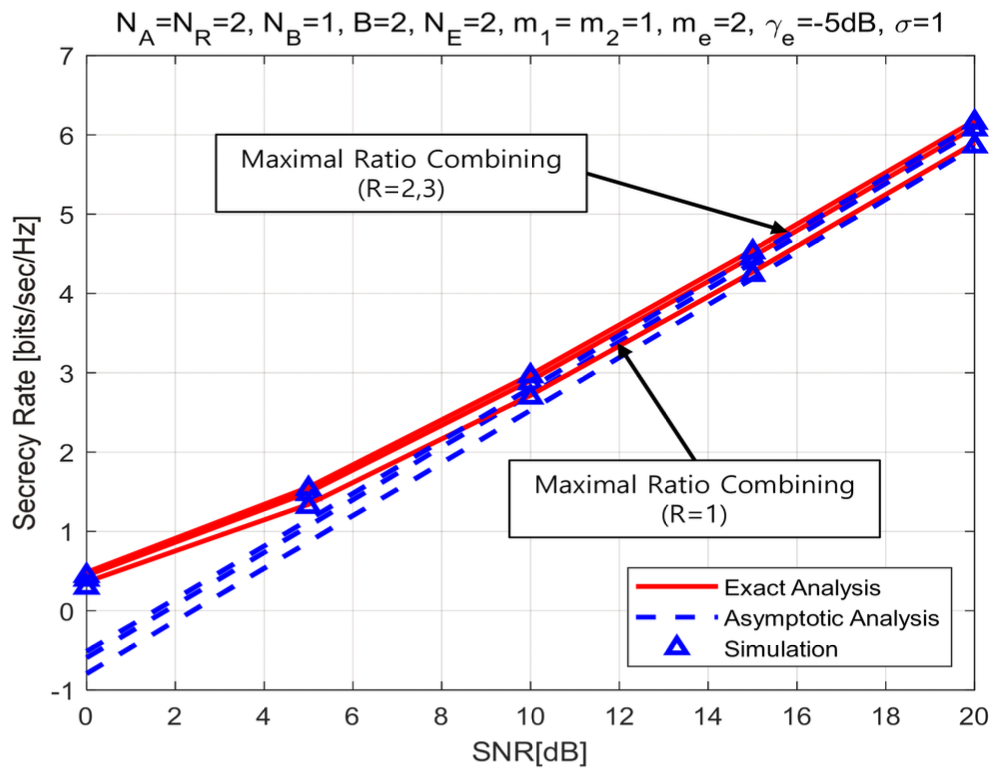
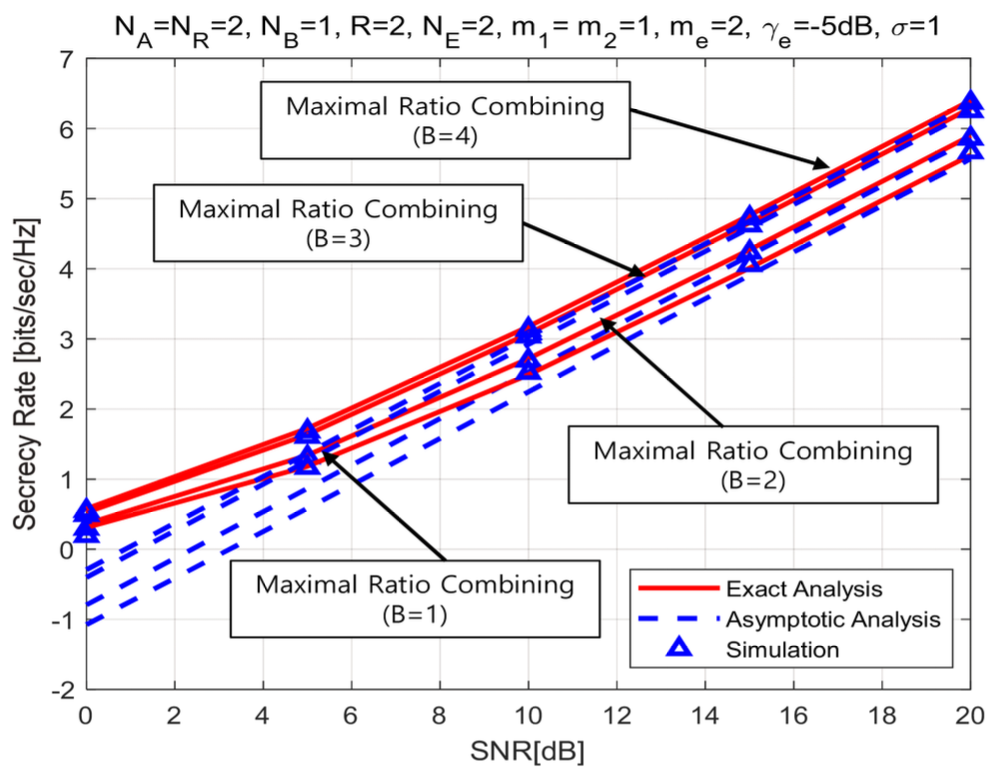
(79)[TeX:] $$\begin{aligned} & C_{\mathrm{sc}}^{\infty}=\log _2 \bar{\gamma}_1+\frac{2}{\ln 2} \sum_{\mathrm{F}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{Fsc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \sum_{P_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}} \sum_{I_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}}\binom{\eta_{\mathrm{F}, \mathrm{sc}}}{k} \\ & \times \Xi_{\mathrm{F}, \mathrm{sc}} \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \bar{\omega}_{\mathrm{F}, \mathrm{sc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)+\frac{1}{\ln 2} \sum_{p_{\mathrm{e}, j} \notin \text { all zero } I_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}} \\ & \times \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \Gamma\left(b_{\mathrm{e}}+1\right) \Psi\left(b_{\mathrm{e}}+1, b_{\mathrm{e}}+1, a_{\mathrm{e}} \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{aligned}$$The analytical expression of asymptotic analysis for the secrecy rate can quantify two important factors of high SNR slope, [TeX:] $$\mathscr{L}_{\mathrm{mc}}$$, in bits/sec/Hz/(3 dB) and high SNR power offset, [TeX:] $$\mathscr{L}_{\mathrm{mc}}^{\infty} L$$, in 3dB units[41]. Using the asymptotic results of Eq.(67) and Eq.(79), this study quantifies the high SNR slope and the high SNR power offset for the proposed triple selection as follows:
and
(81)[TeX:] $$\begin{gathered} \mathscr{L}_{\mathrm{mc}}^{\infty}=-\frac{2}{\ln 2} \sum_{\mathrm{f}, \mathrm{mc}} \sum_{k=0}^{\eta_{\mathrm{f}, \mathrm{mc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r\binom{\eta_{\mathrm{f}, \mathrm{mc}}}{k} \Xi_{\mathrm{f}, \mathrm{mc}} \varpi_{\mathrm{f}, \mathrm{mc}}\left(\bar{\gamma}_1\right) \\ +\frac{1}{\ln 2} \sum_{i_{\mathrm{e}}=0}^{m_{\mathrm{e}} \mathrm{~N}_{\mathrm{E}}-1} \frac{\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{i_{\mathrm{e}}}}{i_{\mathrm{e}}!} \Gamma\left(i_{\mathrm{e}}+1\right) \Psi\left(i_{\mathrm{e}}+1, i_{\mathrm{e}}+1, \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{gathered}$$
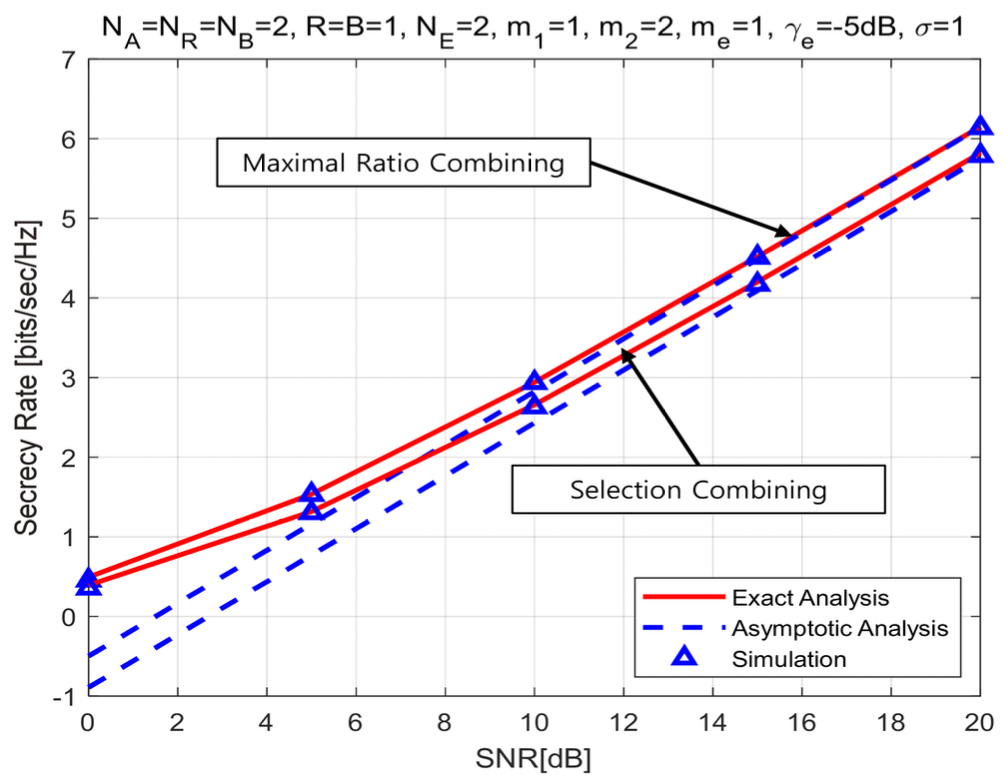
(82)[TeX:] $$\begin{aligned} & \mathscr{L}_{\mathrm{sc}}^{\infty}=-\frac{2}{\ln 2} \sum_{\mathrm{F}, \mathrm{sc}} \sum_{k=0}^{\eta_{\mathrm{Fsc}}} \sum_{r=0}^{\infty} \sum_{l=0}^r \sum_{P_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}} \sum_{I_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}}}\binom{\eta_{\mathrm{F}, \mathrm{sc}}}{k} \\ & \quad \times \Xi_{\mathrm{F}, \mathrm{sc}} \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \varpi_{\mathrm{F}, \mathrm{sc}}\left(\bar{\gamma}_1, \bar{\gamma}_{\mathrm{e}}\right)-\frac{1}{\ln 2} \sum_{p_{\mathrm{e}, j} \notin \text { all zero }} \sum_{\mathrm{e}, \mathrm{~N}_{\mathrm{E}}} \\ & \quad \times \triangle_{\mathrm{e}}\left(\frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right)^{b_{\mathrm{e}}} \Gamma\left(b_{\mathrm{e}}+1\right) \Psi\left(b_{\mathrm{e}}+1, b_{\mathrm{e}}+1, a_{\mathrm{e}} \frac{m_{\mathrm{e}}}{\bar{\gamma}_{\mathrm{e}}}\right) . \end{aligned}$$From above results, we know that the high SNR slope of the triple selection for the secrecy rate is one. It means that the parameters of authorizer and eavesdropper and the fading index of Nakagami fading channel have no impact on the high SNR slope. The effect on the high SNR power offset is analyzed in followed numerical results and discussion section. Ⅳ. Numerical Results and DiscussionsIn this section, we analyze the secrecy rate of the triple selection over Nakagami fading channels using the exact analysis of Eq.(61) and Eq.(73) and the asymptotic analysis of Eq.(67) and Eq.(79). MonteCarlo simulation is performed to prove the exact and asymptotic analysis. In this work, SNR means the average SNR at relay node [TeX:] $$\bar{\gamma}_1$$. Fig.2 and Fig.3 present the secrecy rate of the triple selection with SC as a function of fading index, m 2 and m e over Nakagami fading channels. From Fig.2 and Fig.3, we find that the fading indices of the authorized link and eavesdropper link have no impact on the secrecy rate of the triple selection. Even if affecting the SNR gain of the secrecy outage probability as shown in the work[29] , the fading index is almost independent to both the high SNR slope and the high SNR power offset of the secrecy rate, which is an interesting result. Fig.4-5 plot the secrecy rate of the triple selection as a function of the number of multiple antennas at node (i.e., NR, NB) and eavesdropper (i.e.,NE) over Nakagami fading channels. From Fig. 4 and Fig. 5, we know that the secrecy rate of the triple selection is improved in proportion to the number of multiple antennas at authorized nodes (relay node and user node). This is because MRC at the authorized nodes reduces the power offset. Fig. 4 shows that NR = 3 has a higher offset gain of 1dB compared to NR = 2. In Fig. 5, NB = 2 has a higher offset gain of 1.5dB compared to NB = 1. The high SNR power offset gain between NB = 2 and 3 is about 0.5dB. It can be seen that as NB increases, the high SNR power offset gain decreases. Fig. 6 shows that increasing the number multiple antennas at eavesdropper results in the secrecy rate degradation. This is because SC at eavesdropper increases the power offset. The degradation of secrecy rate is saturated as NE decreases. Fig.4-6 are commonly observed that the high SNR slope is not affected by the number of multiple antennas at authorized node and eavesdropper. Fig.7 and Fig.8 present the secrecy rate of the triple selection with MRC according to the number of relay nodes, R and user nodes, B. Fig.7 shows that the performance of the triple selection increases as the number of number of relay nodes by the relay selection. The case of R=1 has the offset gain of 1dB compared to R=2, while having the identical high SNR slope. It also know that the offset gain converges to zero. We show that the number of user nodes can improve the secrecy rate of the triple selection by the user node selection from Fig.8. The case of B=3 has the offset gain of 2dB compared to B=1 and its gain is reduced to zero. From above results, we confirm that the user and relay selection improves the secrecy rate of the triple scheme in term of the high SNR power offset. Fig. 9 draw the secrecy rate of the triple selection as a function of the combining scheme. From Fig.9, MRC at the authorized node provides the offset gain of 1dB compared to SC at the authorized node. It means that MRC can effectively reduce the power offset. For this reason, the triple selection with MRC provides the better secrecy rate performance than the triple selection with SC. From above all figures, we show that the exact results are well matched to the simulation results at whole SNR region. In addition, the asymptotic results are well matched to the exact results at high SNR region. 4.1 DiscussionThe computational complexity of the proposed triple selection primarily depends on the number of required channel estimations. Specifically, the number of channel estimations for the triple selection is NANRR + NRNBB. In comparison, the dual selection without node selection requires NANR + NRNB estimations, while the dual selection without transmit antenna selection or without receive antenna selection requires NRR + NBB and NAR + NRB estimations, respectively. As demonstrated in numerical results, the secrecy rate increases proportionally with the number of channel estimations. Therefore, a trade-off exists between the secrecy rate and the computational complexity. Ⅴ. ConclusionsThis work investigated the secrecy performance analysis of the triple selection over Nakagami fading channels. This work derived the new exact analytical expressions of the triple selection with MRC and SC for secrecy rate. Using asymptotic results, this work quantified the power offset and the slope for the secrecy rate. From numerical results, we confirmed that the SNR slope is constant regardless of fading index as well as the system parameters of authorizer and eavesdropper. The number of antennas and nodes for the authorizer improves the secrecy rate by decreasing the high SNR power offset. On the contrary, the number of received antennas for the eavesdropper increases the high SNR power offset and deteriorates the secrecy rate. Since imperfect channel condition can affect secrecy performance, we will investigate the imperfect channel estimation and feedback delay on the secrecy performance of the triple selection as part of our future work. BiographyDonghun LeeAug. 2010 : Ph.D., Inform. & Commun. Engineering, Gwan- gju Institute of Science Tech- nology Sep. 2010~Oct. 2015: Senior Member of Engineering, Elec- tronics and Telecommuni- cations Research Institute Nov. 2015~Feb. 2021: Government Officer, Ministry of Trade, Industry and Energy Sep. 2023~Current: Associate Professor, Division of Inform. & Commun. Engineering, Kongju National University <관심분야> MIMO systems, V2X communication and physical layer security [ORCID:0000-0003-0986-6612] References
|
StatisticsCite this articleIEEE StyleD. Lee, "Secrecy Rate Analysis of Dual-Hop Triple Selection AF Relaying Over Nakagami Fading Channels," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 12, pp. 1855-1871, 2025. DOI: 10.7840/kics.2025.50.12.1855.
ACM Style Donghun Lee. 2025. Secrecy Rate Analysis of Dual-Hop Triple Selection AF Relaying Over Nakagami Fading Channels. The Journal of Korean Institute of Communications and Information Sciences, 50, 12, (2025), 1855-1871. DOI: 10.7840/kics.2025.50.12.1855.
KICS Style Donghun Lee, "Secrecy Rate Analysis of Dual-Hop Triple Selection AF Relaying Over Nakagami Fading Channels," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 12, pp. 1855-1871, 12. 2025. (https://doi.org/10.7840/kics.2025.50.12.1855)
|