Ⅰ. 서 론

통신 및 위성 네트워크 기술이 발전함에 따라 차세대 이동 통신 시스템은 전 세계 어디에서나 안정적인 연결성을 제공하는 것을 목표로 하고 있다. 특히, 오지, 해양, 극지방 등의 기존 지상 통신망이 도달하기 어려운 지역에서는 이러한 기술적 요구가 더욱 중요하게 대두되고 있다^[1]. 관련하여 low Earth orbit(LEO) 네트워크는 낮은 고도와 짧은 지연 시간을 가지므로 이러한 환경에 적합하며, 따라서 6G 통신 시스템의 핵심 기술 중 하나로 주목받고 있다^[2]. 하지만 LEO 위성은 고속 데이터 전송과 낮은 지연 시간을 제공 가능한 반면, 좁은 커버리지와 복잡한 네트워크 구성이 요구되기 때문에 커버리지 분석이 중요한 요소로 대두되고 있다.

최근 LEO 위성 연구에서는 푸아송 점 과정(PPP: Poisson point process) 등의 확률 기하(stochastic geometry)를 활용한 커버리지 분석이 활발히 진행되고 있다^[3,4]. 기존의 많은 연구들이 surface 기반의 PPP를 적용하여 스타링크 위성군을 모델링하고 있는 반면, OneWeb 등에서 고려 중인 같은 다중궤도형 위성 통신 모델에 관한 연구는 상대적으로 부족하다. 일부 중요한 연구에서 다중궤도 기반으로 성능 분석 결과를 제시하고 있지만^[5], 사용자의 위치를 고정하는 등 일부 제한된 환경에서의 성능분석이 주로 이루어지고 있다. 또한, 실제 위성 운용 환경에서 발생할 수 있는 각 위성의 비가용성을 고려한 연구 역시 부족한 실정이다.

이에 본 연구에서는 OneWeb 위성군을 기반으로 한 다중궤도형 LEO 위성 네트워크에서 사용자의 커버리지 확률을 실험적으로 분석하는 것을 목표로 한다. 다중궤도형 모델의 경우, 일반적으로 LEO의 각 궤도는 한점에서 모이는 원의 형태로 구성되며, 위성들은 궤도 위에 1차원 PPP를 따라 분포된다^[5]. 본 논문에서는 먼저 이러한 다중궤도 모델이 OneWeb 위성군과 잘 매칭됨을 실측 데이터를 기반으로 검증한다. 추가로, 사용자와 연결된 위성이 비가용 상태에 빠지는 환경을 일정 확률로 반영하여, 기존의 커버리지 확률 모델을 수정하여 정리 하였다. 마지막으로, 위성 밀도의 변화가 커버리지 확률에 미치는 영향을 실험을 통해 분석하고, 실험 결과를 바탕으로 주 연결 위성이 비가용한 경우에도 안정적인 커버리지를 유지할 수 있는 최적의 위성 밀도를 고찰하였다.

Ⅱ. 시스템 모델

본 논문에서는 OneWeb 위성군과 같은 다중궤도형 LEO 네트워크를 고려하기 위해, 고도 h에서 반지름이 R_E인 지구를 둘러싸는 N개의 궤도가 분포한다고 가정한다. 각 궤도에서 위성은 강도 λ_n을 가지는 1차원 PPP를 따르고, 각 궤도에 존재하는 위성의 수는 평균 [TeX:] $$2 \pi\left(R_E+h\right) \lambda_n$$을 갖는 푸아송 분포를 따른다. 위성들의 위치는 각 궤도 내에서 독립적으로 균등 분포한다. 궤도 [TeX:] $$n(n \in\{1, \ldots, \mathrm{~N}\})$$에서 사용자와 가장 가까운 위성 사이의 signal-to-interference ratio (SIR)는 다음과 같다:

여기서 G_ni는 n번째 궤도에 있는 i번째 위성으로부터 사용자까지의 유효 안테나 이득, P는 전송 전력, X_ni는 사용자 u를 기준으로 i번째로 가까운 위성, α는 경로 감쇄 지수를 나타낸다 . 사용자가 위성을 관측할 수 있는 영역을 A라고 정의하고, n번째 궤도마다 A 내부에 존재하는 위성의 개수를 T_n이라고 나타낸다. 또한 , [TeX:] $$\sqrt{H_{n, i}}$$는 위성과 사용자 사이의 채널이며 다음과 같은 나카가미-m 분포를 따른다고 가정한다.

여기서 [TeX:] $$x \geq 0$$, m은 모양 매개변수로 [TeX:] $$m \geq \frac{1}{2}$$를 만족하며, [TeX:] $$\Gamma(m)$$은 감마함수를 나타낸다.

본 연구는 다중궤도 환경에서 위성의 커버리지 확률을 분석하는 것을 목표로 하며, 이를 위해 수신기가 여러 궤도에 분포한 위성들 중 순간적인 SIR이 가장 높은 위성을 선택하는 기회 기반 통신(opportunistic communication) 시나리오를 고려한다. 각 궤도의 위성들은 상호 간섭을 최소화하기 위해 직교 시간-주파수 자원을 활용하여 운용하며, 따라서 커버리지 확률은 다음과 같이 정의된다^[5]:

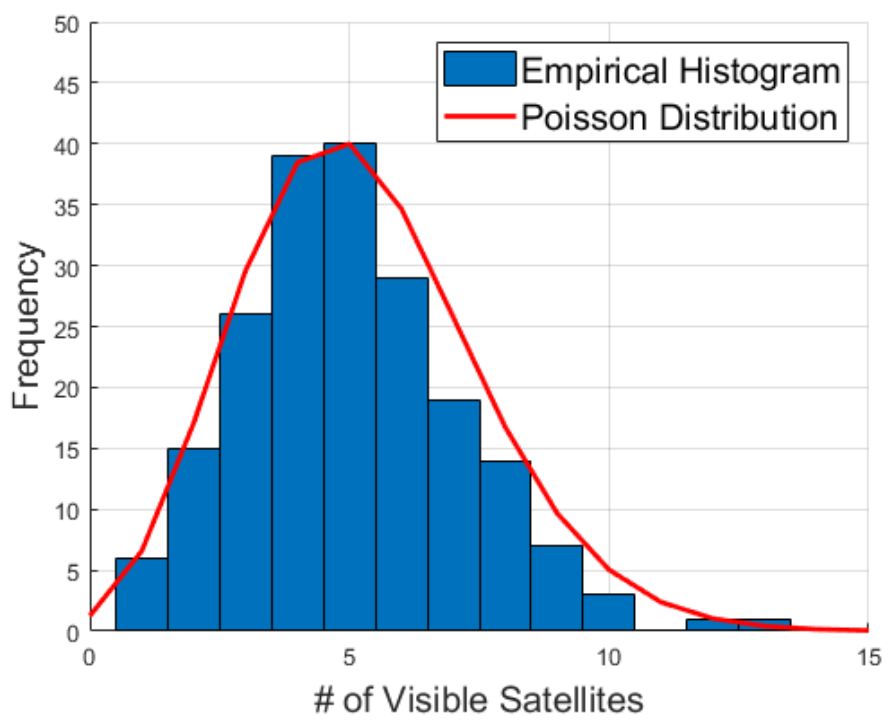
Ⅲ. 제안하는 환경

실험에 사용된 PPP 모델이 OneWeb 위성군을 얼마나 잘 반영하는지 검증하기 위해, [6]에서 제시된 방법을 적용하여 두 모델을 비교하였다. 이를 위해 북위 45도 지역에서 가시적인 위성 데이터를 200개의 무작위 스냅숏으로 수집하였다(데이터 출처: https://satellitemap.space).

그림 1은 하향 링크 사용자가 관측할 수 있는 위성 수에 대한 실험적 분포와 해당 데이터의 평균을 반영한 푸아송 분포를 비교한 결과를 제시한다. 200개의 스냅 숏을 분석한 결과, 실험적으로 얻어진 평균값은 약 5.035로 도출되었으며, 실제 데이터에서 확인된 분포가 푸아송 분포와 높은 유사성을 보이는 것을 볼 수 있다.

그림 1.

PPP 모델의 적절성 검토.(Validity of the PPP model.)

해당 모델에서 위성을 운용하는 과정에서 발생할 수 있는 비가용 상황을 고려하기 위해, 랜덤 변수 Z를 정의하고, 해당 랜덤 변수 가임계 값(threshold) T보다 크면 비가용 상황이 발생되었다고 가정하였다. 또한, 위성의 비가용 상황은 시스템의 다양한 요소들이 확률적으로 결합되어 발생할 수 있으므로, 랜덤변수 Z는 표준정규분포를 따른다고 가정하였다. 이러한 가정을 기반으로 식 (3)에서 정의된 기존의 커버리지 확률을 위성 비가용성을 반영한 형태로 다음과 같이 재정의한다:

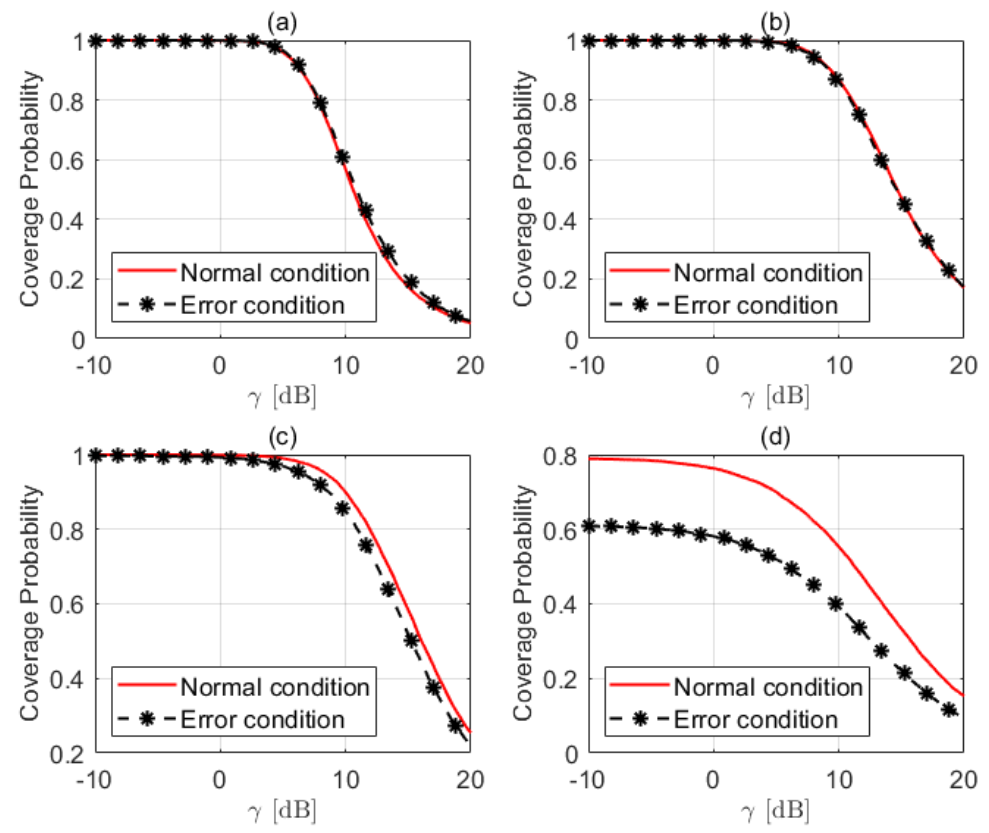
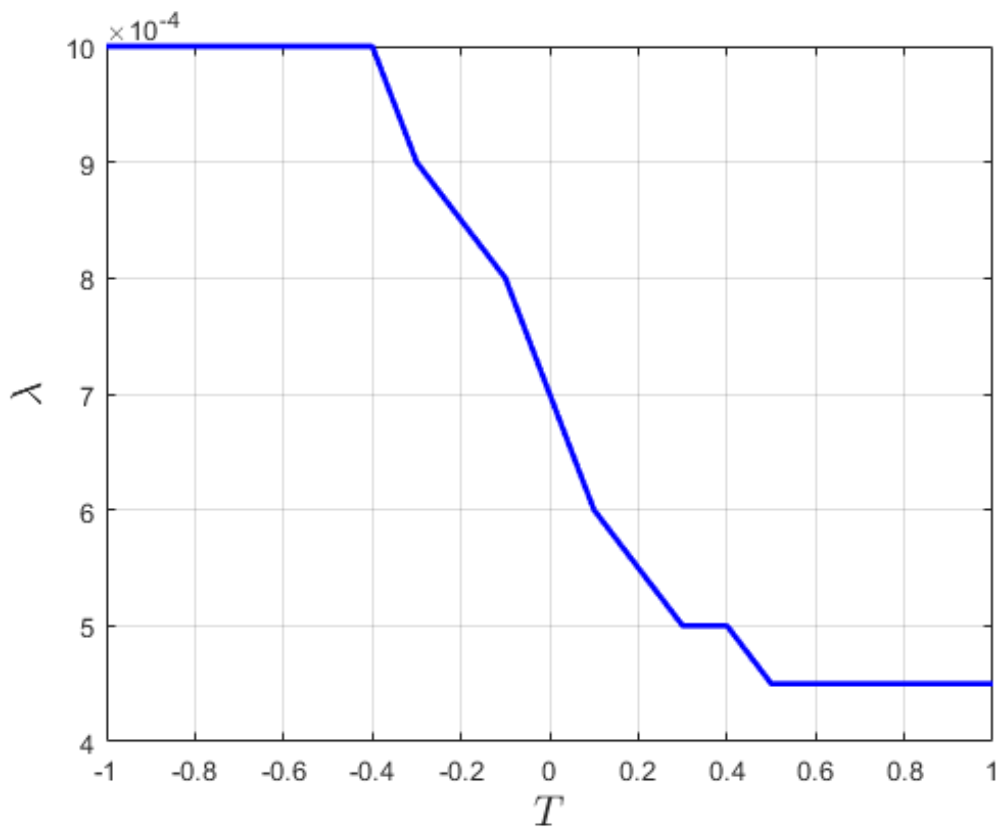
여기서 사용자와 가장 가까운 위성이 비가용되는 상황일 때의 커버리지 확률을 [TeX:] $$P_{c o v}^{\text {fail }}$$로 나타내었다.

Ⅳ. 시뮬레이션 결과 및 결론

본 장에서는 이전 장의 수식을 기반으로 다중궤도형 하향 링크 위성 네트워크에서 커버리지 확률을 분석한다. 시뮬레이션 툴로는 MATLAB을 활용하였으며 시뮬레이션 환경은 III절의 내용을 기반으로 OneWeb의 저궤도 위성 시스템 환경과 유사하게 구축하여 몬테카를로 기법을 통해 커버리지 확률을 도출하였다.

그림 2는 사용자가 가장 가까운 1번 위성과 통신하는 정상 상황과, 첫 번째로 가까운 위성이 통신이 불가능해 두 번째 위성과 통신하는 비가용 상황에서의 커버리지 확률을 비교한 결과이다. 모든 실험에서 R_E=7850, h=1500, m=1, α=2, N=12, T=-0.5으로 설정하였다. 위성의 밀도는 다음과 같이 설정하였다: (a) λ=0.001(궤도당 약 50개 위성), (b) λ=0.0005(궤도당 약 25개 위성), (c) λ=0.0003(궤도당 약 15개 위성), (d) λ=0.0001(궤도당 약 5개 위성). 위성 밀도가 낮아질수록 첫 번째 위성이 비가용인 상황에서 커버리지의 감소폭이 커지는 것을 확인할 수 있다. 또한, λ=0.0001 이하에서는 평균 위성 수가 급감하면서, 커버리지 성능이 현저히 저하되는 현상을 확인할 수 있다. 이는 사용자 가시 영역(A) 내에 위성이 존재할 확률이 급격히 감소하기 때문이다. 따라서 위성이 비가용 상태에 빠질 수 있는 환경에서 coverage 성능을 일정 레벨 이상으로 유지하기 위해서는 위성의 밀도를 일정 값 이상으로 유지할 필요가 있다.

그림 2.

위성 비가용 상황에서 커버리지 확률 분석.(CoverageProbabilityAnalysis)

본 논문에서는 이러한 위성의 비가용 상황에서 통신 품질을 안정적으로 유지하기 위하여, 커버리지 확률 관점에서의 최적 위성 밀도를 정의한다. 이를 위해 위성이 가용상태와 비가용 상태일 때의 커버리지 성능을 비교하였고, 그 차이가 특정 기준 이하로 유지되는 위성밀도를 실험적으로 탐색하였다. 특히 SNR이 15dB일 때 두 상황 간의 커버리지 확률 차이가 0.05 이하로 유지되는 경우를 실험적으로 관찰하여, 이때의 최소 위성 밀도를 실용적인 최적값으로 간주하였다. 여기서 0.05(5%)라는 기준은 통신 품질 관점에서 성능 저하를 체감하기 어려운 수준의 차이를 반영한 값이다. 즉, 위성의 가용/비가용 상태 간 커버리지 차이가 5% 이내라면 두 상황 간의 성능 차이를 무시할 수 있다고 판단하였다.

그림 3은 임계값의 변화에 따른 최적의 밀도를 그래프의 형태로 표현하였다. 여기서 위성의 최대 밀도값은 0.001이다. 일반적으로 임계값이 낮을수록(즉, 위성 비가용 확률 Q(T)가 높을수록) 커버리지 손실을 보완하기 위해 더 높은 위성 밀도가 요구되며, 임계값이 높을수록 상대적으로 낮은 밀도에서도 안정적인 커버리지가 유지된다. 이러한 결과는 임계값과 위성 밀도 간의 상충 관계를 보여주며, 이를 통해 다중궤도형 LEO 위성 네트워크에서 안정적인 커버리지를 확보하려면 최적의 위성 밀도가 중요함을 확인할 수 있다.

그림 3.

위성 밀도 vs.T; SNR = 15[dB].(Lambda vs. T; SNR = 15[dB].)