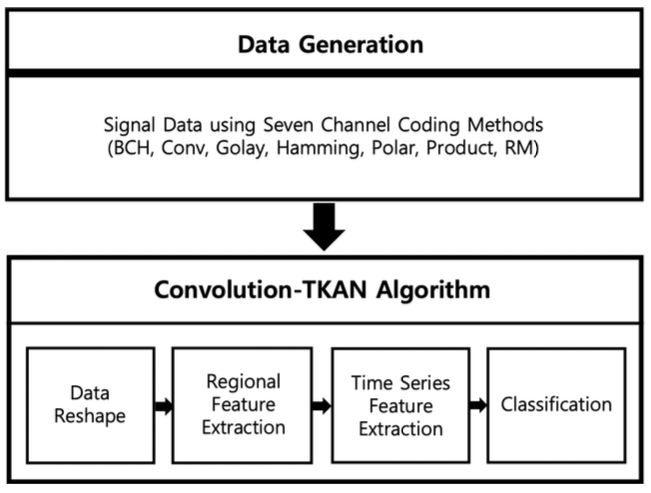
Ⅰ. 서 론

신호에 대한 사전정보를 알 수 없는 비협조적인 상황 인 사이버전자전에서 채널코딩을 자동으로 인식하는 기술이 최근 활발히 연구되고 있다. 이러한 기술은 사이 버전자전에서 적군의 신호를 탈취해 정보를 습득하기 위해 활용되고 있다^[1]. 민간 무선통신 분야에서는 사전 정보를 전송하면 추가로 대역폭이 필요하기 때문에 사 전정보가 필요없는 자동 채널코딩 인식의 중요성이 부 각되는 상황이다.

채널코딩을 자동으로 인식하는 방법은 신호처리 기 술을 이용하거나 딥러닝 혹은 신호처리와 딥러닝을 하 이브리드한 기술을이용할 수 있다. 신호처리 기술응용 에서는 푸리에 변환이 대표적으로 사용된다. [2]는 갈루 아 필드 푸리에 변환을 기반으로 채널코딩 인식기법을 제안했다. 제안한 기법은 BCH 코드의 특징인 연속근과 근이 제로 스펙트럼과 일치한다는 사실을 이용한다. 연 속 제로 스펙트럼 값이 제로 스펙트럼 성분의 확률로 도출된 임계값 조건을 만족하는 경우 코드 길이를 추정 할 수 있다. 또한, 계산량이 기존 푸리에 변환에 비해서 60% 정도로 적다. 하지만 이 방법은 BCH 코드에만 한정되어 있어 다양한 채널코딩 유형을 적용하기에는 적합하지 않은 단점이 있다.

딥러닝을 이용하는 기법으로는 RNN, CNN, BERT 모델이 대표적으로 사용된다. [3]은 RNN 기반 자동 채 널코딩 인식기법을 제안했다. 특히, RNN의 가중치 초 기화 매커니즘을 개선하여 가중치 소멸 현상을 해결했 으며, 신호의 시계열 특성을 추출하여 CNN, MLP와 같은 벤치마크 모델보다 높은 성능을 얻었다. 하지만 제안한 기법은 장기 의존성 문제가 발생한다는 단점이 있다. [4]는 병렬 1차원 CNN 기반 자동 채널코딩 인식 기법을 제안했다. 저자는 병렬 구조의 4개 콘볼루션 층 과 Concatenate층 그리고 MaxPooling층을 하나의 인 셉션 모듈로 개발했다. 제안한 인셉션 모듈을 여러 개 연결하여 전체 네트워크를 구성했다. 제안한 기법은 평 균 실행 속도가 동일 크기의 RNN에 비해 빠르지만, RNN 기반 기법보다 채널코딩 인식 정확도가 평균 10% 낮았다. [5]는 BERT 기반 자동 채널코딩 인식기법을 제안했다. 저자는 일반적인 CNN은 제한적인 커널 크 기로 인해 특징 추출 능력을 향상하기 힘들다고 하였다. 이를 해결하기 위해 신호 비트스트림을 자연어로 인식 해 특정 길이만큼 시퀀스로 잘라서 처리했다. 그리고 트랜스포머의 변형 모델이면서 문장 의미 추출에 강점 이 있는 BERT를 사용했다. 일반적인 트랜스포머는 인 코더와 디코더로 이루어져 있는데, BERT는 디코더를 제외하고 인코더만 사용한 모델이다. 처음에는 각 시퀀 스를 독립적인 임베딩 벡터로 전환하고 위치 정보를 추 가하는 위치 인코딩 과정을 거친다. 다음으로 쿼리, 키 정보를 이용해 정보를 추가 추출하는 어텐션 층을 거치 고 최종 분류를 수행한다. 정확도는 CNN과 비딥러닝 방법인 GJETP 기법보다 높지만, 모델의 복잡도가 높을 뿐 아니라 입력 코드 길이가 길어질수록 임베딩 벡터의 종류도 다양해지므로 복잡도가 계속 증가하는 단점이 있다.

하이브리드 기법은 기존 신호처리 기술과 딥러닝 기 법을 결합하는 방법이 대표적으로 사용된다. [6]은 딥러 닝 모델인 MLP와 기존 신호처리 기술인 BCJR 알고리 즘의 장점을 결합한 방법을 제안했다. BCJR 알고리즘 은 Polar, LDPC 코드에서 주로 사용하는 디코딩 알고 리즘이다. MLP 신경망은 채널 코드 유형을 인식하고, BCJR 알고리즘은 디코딩을 수행한다. 하지만, 딥러닝 모델 이식과 별도의 하드웨어 설치 등으로 인해 복잡성 이 높다는 단점이 있다.

본 논문은 딥러닝 기법을 이용한 Convolution- TKAN 기반 자동 채널코딩 인식 알고리즘을 제안한다. 해당 알고리즘은 CNN, TKAN 모델의 장점을 효율적 으로 결합했다. TKAN은 KAN^[7]의 변형 모델으로 RNN처럼 시퀀스별로 KAN 기반 병렬 학습이 진행된 다[8]. 그리고 게이팅 매커니즘을 통해 장기 의존성 문제 도 예방한다. TKAN은 신호 데이터의 시계열 특징을 추출한다. 콘볼루션 층은 TKAN의 시퀀스 길이를 넘어 서는 채널코딩별 지역적 특징 추출을 수행한다. 결론적 으로 Convolution-TKAN 네트워크는 지역적, 시계열 특징까지 모두 추출이 가능하여 다양한 채널코딩 유형 에서 탁월한 성능을 나타낸다.

Ⅱ. Convolution-TKAN 기반 자동 채널코딩 인식

그림 1은 본 논문에서 채널코딩을 자동으로 인식하 는 전체적인 흐름도이며, 'Data Generation', 'Convolution-TKAN Algorithm' 2단계로 구성한다. 채널코딩은 BCH, Convolution, Golay, Hamming, Polar, Product, Reed-Muller 7개를 사용했다. 'Data Generation'에서는 채널코딩된 데이터를 파이썬의 Numpy 파일로 저장 및 관리한다. 'Convolution-TKAN Algorithm'에서는 1차원 입력 데이터를 2차원으로 Reshape하고, 다양한 커널을 가진 콘볼루션 층과 TKAN을 이용하여 지역적 특징과 시간적 특징을 각각 추출한다. 마지막으로 Dense층을 통해 채널코딩 유형 을 분류한다.

그림 1.

제안한 시스템 구조

2.1 데이터 생성

본 논문에선 파이썬을 이용해 신호 데이터를 생성했 다. 7가지 채널 코딩 유형의 자세한 파라미터는 표 1에 정리했다. 채널은 AWGN(Additive White Gaussian Noise)을 사용했으며, SNR(Signal-to-Noise Rate)은 -5dB부터 20dB까지 1dB 간격으로 설정했다. 모델학 습에 사용한 데이터는 복조까지 거친 정수 데이터를 사 용했다. 전체 데이터셋 샘플 수는 SNR 1개당 1000개 로, 총 147000개이다. 데이터 길이는 정확도와 복잡도 측면에서 제일 우수했던 512 bit로 설정했다.

2.2 KAN

KAN(Kolmogorov-Arnold Networks)은 Kolmogorov- Arnold 정리를 응용하여 MLP의 유력한 대안으로 2024 년 처음 제안^[7]된 네트워크이다. Kolmogorov-Arnold 표현 정리는 식(1)과 같다.

식(1)의 [TeX:] $$\begin{equation} \phi \end{equation}$$는 처음 엣지의 활성화 함수를 의미하고, [TeX:] $$\begin{equation} \Phi \end{equation}$$는 두 번째 엣지의 활성화 함수를 의미한다. p는 처음 엣지의 입력 데이터 순번을 의미하고, q는 두 번째 엣지 의 입력 데이터 순번을 의미한다. n은 실제로 입력되는 데이터의 개수를 의미한다. 즉, 처음 엣지의 활성화 함 수들을 거친 값을 합해서 다시 두 번째 엣지의 활성화 함수의 입력값으로 사용해 KAN의 최종 출력값을 내는 것이다.

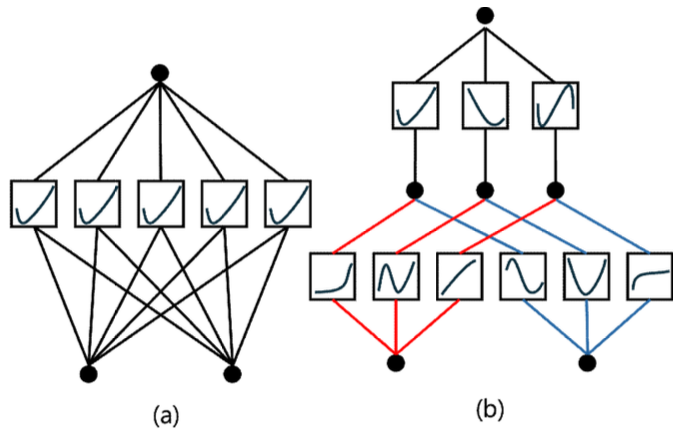
또한, n차원 다변량 함수를 n개의 단변량 함수의 합으로 표현했다. 기계학습 관점에서 보면 기존 하나의 n차원 다변량 함수를 학습시키던 방식을 n개의 단변 량 함수를 학습하는 것으로 표현이 가능하다는 뜻이다. 즉, 층내부에서 n개의 각자 다른 단변량 활성화 함수 를 사용할 수 있다는 것이다. 식 (2)의 w는 활성화 함수 의 출력값을 조절하기 위해 사용되는 factor이다. [TeX:] $$\begin{equation} b(x) \end{equation}$$ 는 기저 함수라고 불리며, [TeX:] $$\begin{equation} \frac{x}{1+e^{-x}} \end{equation}$$의 silu 활성화 함수로 주어진다. 식 (3)의 [TeX:] $$\begin{equation} B(x) \end{equation}$$는 B-Spline으로 주어 진 여러 개의 점에서 정의되는 곡선 다항식이고, c는 각 B-Spline의 계수이다. i는 일정한 구간 중에서 점의 순번이다. 마지막 합을 통해 [TeX:] $$\begin{equation} \text { spline }(x) \end{equation}$$는 다항식의 선 형 결합으로 이루어진다.

그림 2는 MLP와 KAN을 그래프 구조로 비교해 놓 은 그림이다. MLP는 각 노드에 층마다 동일한 활성화 함수가 대응되고 각 엣지에 가중치 행렬을 대응시킨다. 하지만 KAN은 각 노드에 함수값이 대응되고 각 엣지 에 활성화 함수가 대응된다. 또한, MLP처럼 노드끼리 Fully-Connected 되어있는 구조가 아닌 식 (1)의 q값 이 같은 엣지의 활성화 함수끼리만 합해서 노드값을 구 성한다는 차이점이 있다. 그리고 KAN은 활성화 함수 를 학습시킬 수 있고, 이는 크게 'Residualactivation functions'와 'Initialization'으로 구성된다.

그림 2.

KAN과 MLP 구조 비교 ^[7] (a) MLP (b) KAN

Residual activation functions은 식 (2)의 [TeX:] $$\begin{equation} b(x) \end{equation}$$가 re- sidual connection 역할을 수행한다. [TeX:] $$\begin{equation} b(x) \end{equation}$$는 silu 함수 로 학습이 가능한 함수가 아니기 때문에 [TeX:] $$\begin{equation} \text { spline }(x) \end{equation}$$가 모든 비선형성을 표현할 수 있어야 한다. 식 (3)의 [TeX:] $$\begin{equation} B(x) \end{equation}$$는 고정된 함수이므로 결국 계수인 c를 업데이 트 함으로써 비선형성을 표현한다. Initialization에서는 Xavier 함수가 [TeX:] $$\begin{equation} \text { spline }(x) \end{equation}$$의 값이 0에 수렴하는 방향 으로 w를 초기화한다. 이때 각 c는 N정규분포로부터 샘플링하는 것으로 업데이트된다.

KAN은 MLP보다 정확도와 복잡성에 대해 더 높은 파레토 최적을 달성한다^[7]. 또한 MLP는 같은 활성화 함수를 계속해서 사용하여 발생하는 전역성 때문에 새 로운 domain 문제를 학습하면 이전 풀이를 보존하지 못하는 문제가 있다. 그러나 KAN은 새로운 domain 문제를 해당 데이터 영역 내에서만 해결하는 지역성 때문에 이전 단계의 학습을 잘 보존한 다. 그리고 Python에서는 사용자가 [TeX:] $$\begin{equation} B(x) \end{equation}$$의 다항식 차 수인 spline-order와 [TeX:] $$\begin{equation} B(x) \end{equation}$$의 개수인 grid를 지정할 수 있어 더 다양한 네트워크의 표현이 가능하다^[11]. 이 외 에도 KAN을 이용한 회귀 문제에서는 학습된 함수를 하나의 방정식으로 해석할 수 있고^[12], 노드의 pruning 이 자동으로 가능하다는 장점이 있다.

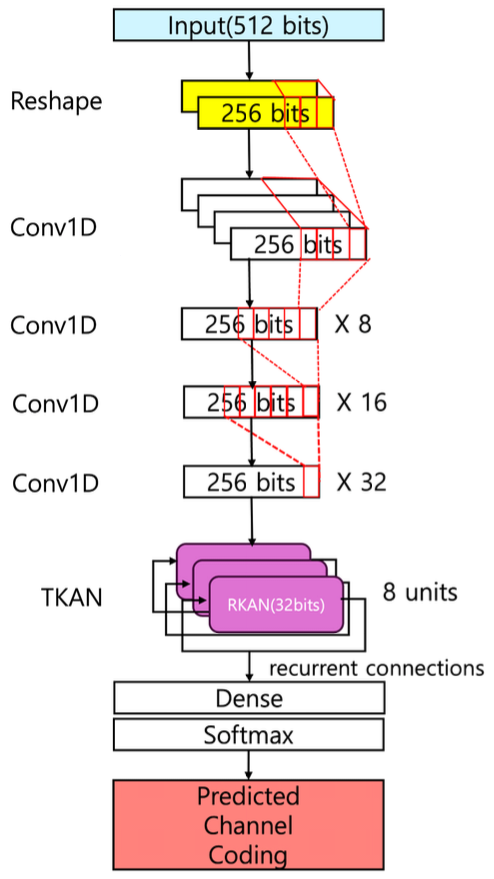
하지만 KAN은 다수의 단변수 함수로 나뉜 복잡한 계산 방식을 가지고 있어 GPU에서 잘 병렬화되지 않으 며, 연산 성능이 다른 신경망에 비해 떨어진다. 그리고 다수의 단변수 함수를 가지기 때문에, 이 구조를 최적화 하는 과정에서 각 단변수 함수의 역할과 관계가 복잡해 진다. 결과적으로 지역 최적해에 수렴하여 모델을 최적 화하기 어려울 수 있는 단점이 있다.

2.3 TKAN

TKAN (Temporal KAN)은 KAN에 RNN과 LSTM 의 매커니즘을 결합한 모델이다^[8]. TKAN은 KAN의 단점이었던 최적화 문제를 개선했고, 시계열 특징까지 추출했다. 그림 3은 TKAN의 구조이고 'RKAN'과 'Gating mechanism' 두 부분으로 구성한다. RKAN은 KAN처럼 노드가 나열되어 있으면서도, RNN처럼 데 이터를 시간 순서대로 시퀀스로 나눠서 처리한다. 그리 고 각 엣지에서 활성화 함수는 시간 변수와 은닉값을 활용하여 계산한다. Gating mechanism은 입력 데이터 의 길이가 길어질수록 초기 정보의 가중치는 옅어지는 장기 의존성 문제를 해결하기 위해 제안되었다. TKAN 은 forget, input, output 게이트로 총 3가지 게이트를 사용한다. forget 게이트는 이전 상태에서 잊을 정보를 결정하고, input 게이트는 새롭게 포함할 정보를 결정하 며, output 게이트는 출력할 정보를 결정한다. 최종적으 로 셀 상태는 forget, input 게이트를 통해 계산되고, 셀 상태는 output 게이트에서 은닉값을 계산하는 데 쓰이 며, 최종 출력값은 은닉값을 이용해 계산한다.

그림 3.

TKAN 구조도 ^[8] (a) MLP (b) KAN

TKAN을 GRU, LSTM과 비교 실험했을 때, 5번 학 습시킨 후 테스트 손실을 비교하면 TKAN, GRU, LSTM의 손실은 각각 4.874e-03, 4.890e-03, 7.573e-03 으로 TKAN의 손실 결과가 GRU, LSTM보다 낮았다. 학습/검증에서는 손실 결과가 GRU, LSTM과 유사했 다. 이는 TKAN이 일반적인 RNN 계열 네트워크와 같 거나 그 이상의 성능을 가진다는 것을 증명한다^[8].

하지만 TKAN은 KAN의 복잡한 구조와 시계열 데이터를 처리하는 과정 때문에 각 시퀀스 단계마다 함 수 근사를 수행하는 학습 과정에서 시간과 자원이 많이 소모된다. 또한, TKAN은 공식적으로 GPU를 이용한 학습을 지원하지 않는다는 단점이 존재한다.

2.4 Convolution-TKAN

그림 4는 제안한 Convolution-TKAN 네트워크의 구 조이고, Reshape, 지역적 특징 추출, 시계열 특징 추출, 분류 4단계로 구성한다.

2.4.1 Reshape

Convolution-TKAN의 첫 단계는 입력 데이터의 차 원을 변경하는 것이다. 콘볼루션 1D, TKAN 층 모두 입력을 2차원으로 받기 때문에 그에 맞춰 512bits의 1 차원 비트스트림 데이터를 (256, 2)의 2차원 데이터로 변환한다. 모델을 거치면서 콘볼루션 1D층은 이 데이 터를(특성 수, 채널수)로, TKAN층은 (시퀀스 수, 특성 수)로 받는다.

2.4.2 지역적 특징 추출

두 번째 단계는 콘볼루션 1D 층을 이용해 붙어있는 비트들의 지역적 특징을 추출한다. 다양한 특징 추출을 위해, 콘볼루션 연산의 커널 사이즈 파라미터를 (3, 4, 5, 6)으로, 필터 수 파라미터도 (4, 8, 16, 32)로 설정했 다. 또한, 기울기 소멸 및 폭증 문제를 방지하기 위해 각 콘볼루션 층에서는 Relu 활성화 함수와 he_normal 가중치 초기화 방법을 사용한다.

그림 4.

Convolution-TKAN 모델 구조도

2.4.3 시계열 특징 추출

세 번째 단계는 TKAN 층을 이용해 시계열 특징을 추출한다. TKAN에서는 RNN처럼 입력 데이터를 시퀀 스 단위로 나눠서 따로 은닉값을 계산한다. 이전 시퀀스 정보를 참고하므로 채널 인코딩 패턴을 학습하는 데 추 가로 도움을 준다. 그리고 직전의 콘볼루션 층으로부터 TKAN으로 들어오는 데이터가 (256,32) 차원으로 길 이가 256 * 32 = 8192로 길다. 그래서 장기 의존성 문제가 발생할 가능성이 있지만 이는 TKAN의 게이팅 매커니즘으로 개선이 가능하다. 이 외에도 TKAN의 출 력 노드 수인 units 파라미터는 8로 설정하고, 다음 층이 TKAN층이 아니므로 return_sequences 파라터는 False로 설정해 비시퀀스 값으로 전달했다.

2.4.4 분류

Dense층은 선형적인 정보를 분류한다. 7개의 노드와 softmax 활성화 함수를 거쳐 채널코딩 유형을 분류한 다. softmax 함수는 출력을 각 클래스별 확률값으로 반 환한다. 해당 구조들을 통해 채널코딩 유형을 효과적으 로 예측할 수 있다. 본 모델은 다양한 특징 추출 층 사용 으로 각기 다른 채널 인코딩 패턴 학습에 강점이 있으 며, 기울기 소멸 및 폭증, 장기 의존성 문제와 같은 부가 적인 문제 해결에도 효과적이다.

Ⅲ. 시뮬레이션및성능평가

3.1 실험 환경

표 2는 Convolution-TKAN 기반 7가지 채널코딩 유 형 예측 시뮬레이션에 쓰이는 하이퍼 파라미터 목록이 다. 딥러닝 모델 외적으로 학습에 쓰이는 하이퍼 파라미 터만 기술했다. 전체 데이터는 훈련, 테스트, 검증 데이 터를 위해 각각 64:20:16 비율로 나눴다. 옵티마이저 는 Adam을 사용하였고, 학습률은 0.005로 고정했다. 에포크는 200번으로 설정해주었고, 배치 사이즈는 32 를 사용했다. 학습 중 검증 손실이 몇 회 이상 연속으로 감소하지 않으면 학습을 바로 종료하는 조기 종료의 pa- tience 파라미터는 10으로 설정해주었다. 반복 실험해 본 결과, 손실 그래프가 빠르게 과적합 되는 것이 아닌 진동하면서 천천히 줄어드는 추이를 보였다. 그래서 학 습이 최대한 개선되기 전에 멈추지 않도록 에포크와 조 기 종료 patience는 위와 같이 크게 설정해주었다.

실험 PC의 CPU, GPU, 그리고 메모리는 각각 Intel Xeon CPU E5-1650 v4와 NVIDIA GeForce RTX 4090, 32GB를 사용했으며, 운영체제는 Windows 11이다.

3.2 실험 결과

표 3은 TKAN 층의 tkan_activations 인수에 따른 Convolution-TKAN의 파라미터 수와 정확도 비교 표 이다. 하나의 중괄호 속 인수가 하나의 TKAN 유닛의 spline-order와 grid에 각각 할당된다. 중괄호 수와 두 인수가 증가하면 모델의 총 파라미터수와 평균 정확도 가 비례해서 증가함을 알 수 있다.

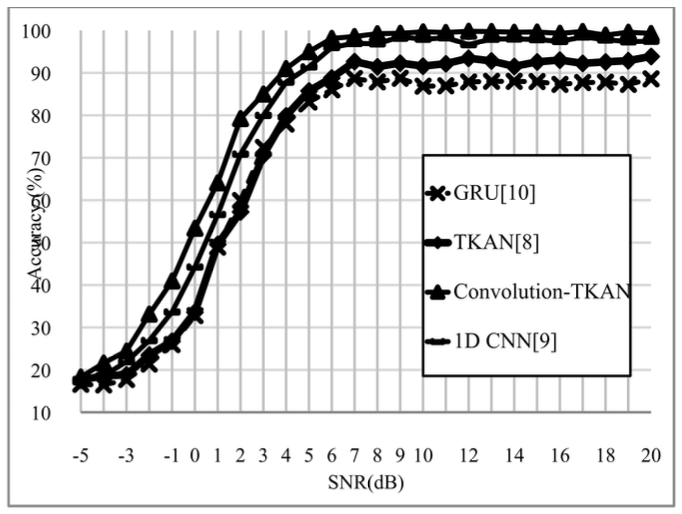
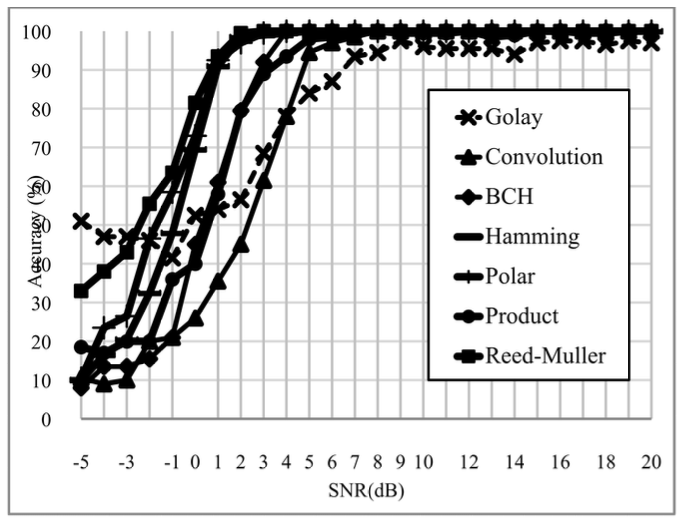
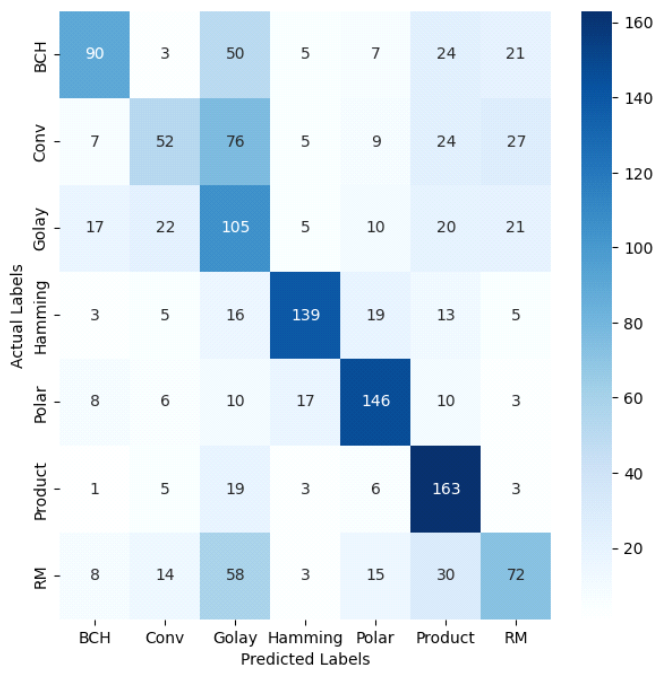
하지만 TKAN은 학습할 때 GPU를 지원하지 않으므 로 Convolution-TKAN 모델도 학습할 때 GPU를 활용 할 수 없다. 만약 강제로 GPU를 사용해도 TKAN은 단변수 함수로 나누어진 구조이므로 병렬 처리 효율이 낮아서 타 딥러닝 모델보다 같은 파라미터 대비 학습 시간이 매우 느리다. 그 결과 파라미터 수 10,000부터는 학습 시간이 약 620분으로 정상적인 학습 시간을 훨씬 상회하여 증가했다. 따라서, 인수는 복잡도와 정확도를 모두 만족하는 {3,10}, {2,5}, {1,3}를 선택했다. 또한 TKAN은 수많은 단변수 함수들의 조합을 통해 결과를 도출하므로 복잡한 문제는 예측 결과 해석이 매우 어 렵다.

그림 5는 벤치마크 모델과 Convolution-TKAN 모델 의 SNR-정확도를 비교한 그래프이다. Convolution-TKAN 모델은 2번째로 평균 정확도가 높 은 TextCNN 모델보다도 모든 SNR 구간에서 평균 3% 정도 정확도가 높았다. Convolution-TKAN은 SNR이 2dB일 때 정확도 79.21%로 TextCNN과 약 8%의 제일 큰 차이가 난다. 2dB는 AWGN의 Noise-Power와 Signal-Power가 동일해지기 직전의 구간인데, 이때 모 델 중 가장 높은 정확도를 보이는 것은 Convolution- TKAN이 채널 인코딩 패턴과 노이즈를 합친 비선형성 에 강인하다는 것을 입증한다.

그림 5.

타 모델과 Convolution-TKAN 정확도 비교

콘볼루션 코드는 인코딩 이전 정보가 현재 인코딩에 영향을 미치므로 시퀀스 간 특징이 뚜렷하게 존재하기 때문에 TKAN을 이용해 시계열 특징 추출에 유리하다. 반면 나머지 BCH, Hamming, Polar, Product, Reed-Muller, Golay의 블록 코드들은 한 번 인코딩 이 후에는 그 결과가 다음 인코딩에 영향을 미치지 않아 정해진 길이 안에만 특징이 존재하기 때문에 다양한 필 터 사이즈를 가진 Convolution 층들을 이용한 지역적 특징 추출에 유리하다. 따라서 제안한 기법의 향상된 정확도 결과가 나온 이유는 다양한 채널코드의 여러 인 코딩 방식을 1차 Convolution 층, 2차 TKAN 층에서 전부 학습하기 때문이다. 또한, Convolution-TKAN 모 델이 1D CNN보다 높은 정확도를 보이는 이유는 1D CNN은 Convolution 층 이후 Max나 Average 연산으 로 특징 크기를 줄이는 Pooling 층을 사용하지만, Convolution-TKAN은 TKAN이 크기를 줄일 뿐 아니 라 순환 연산과 KAN 연산을 추가로 수행하기 때문이다.

이 외에도 단독 TKAN과 GRU 모델은 서로 정확도 가 유사하지만 High SNR 구간에서는 TKAN이 앞서는 것을 볼 수 있다. 이 결과는 층수, unit 수 등의 설정이 모두 동일하지만 활성화 함수의 다양성의 차이로 인한 것이다.

그림 6과 7은 Convolution-TKAN 모델의 코드별 정 확도 그래프와 SNR 0dB일 때의 혼동행렬이다. 그래프 를 보면 RM, Golay, Convolution 코드를 비교적 잘 분류해내지 못한다. RM, Golay 코드는 꽤 복잡한 생성 매트릭스를 가지고 있고, Convolution 코드는 이전 정 보를 기억하는 메모리를 추가로 가지고 있어 분류하기 간단한 구조는 아니다. 그런데 노이즈와 원신호를 구분 할 수 없어지는 SNR0dB 이하 구간에서는 패턴을 오인 식할 확률이 높아 더욱 힘들다.

그림 6.

Convolution-TKAN 코드별 정확도 비교

그림 7.

SNR이 0dB일 때 혼동행렬

Ⅳ. 결 론

본 논문은 Convolution-TKAN 모델을 이용하여 다 양한 채널코딩을 자동으로 인식하는 알고리즘을 제안 했다. Convolution-TKAN 모델은 다양한 커널을 가지 는 콘볼루션 층을 이용해 신호 비트스트림의 지역적 특 징을 추출한다. 그리고 추출한 특징 데이터를 TKAN에 서 시퀀스 단위로 처리해 시퀀스 간 연관성을 학습하고 최종적으로 채널코딩 유형을 예측한다.기존 딥러닝 연 구에서 많이 쓰였던 MLP보다 KAN이 파라미터 수는 적으면서 더 다양한 비선형성을 학습할 수 있으므로 KAN은 MLP를 대체하기에 충분한 모델이다. 결론적 으로 제안한 모델은 비교적 낮은 깊이를 가짐에도 뛰어 난 채널코딩 유형 분류 성능을 보이고, TKAN을 단독 으로 사용했을 때도 성능이 우수하지만, 콘볼루션 층 이후에 사용했을 때 더 좋은 성능을 보이므로 이미 추출 한 특징의 후처리에 더 적합하다고 볼 수 있다.