MVDR(minimum variance distortionless response) 빔포머(beamformer)는 원하는 신호의 도래각 정보를 이용하여 이 방향으로 빔 이득을 1로 하면서 어레이 (array) 출력 전력이 최소가 되도록 가중벡터(weight vector)를 조정한다. 도래각 정보가 정확하다면 MVDR 어레이는 출력 SINR(signal-to-interference-plus-noise ratio)을 최대로 할 수 있다. 그러나 도래각 정보에 오류 가 있다면 원하는 신호도 제거해야 할 간섭신호로 간주 되어 심한 성능저하가 발생될 수 있다^[1].

BPSK(binary phase shift keying) 또는 UQPSK (unbalanced quadrature phase shift keying)처럼 신호 가 비회전성을 가지면, 이를 이용하여 빔포머 성능을 좋게 할 수 있다. 비회전성에 따른 성능개선을 도모하기 위해, WL(widely linear)^[2-11] 방식을 도입한다. WL 방 식에서는 어레이 수신벡터와 이의 켤레 복소(complex conjugate)벡터를 결합한 확장수신벡터로부터 출력을 구한다. 이때, 충분한 성능개선을 이루기 위해서는 원하 는 신호에 대한 확장조향벡터를 구하는 것이 필요하다.

확장조향벡터는 원하는 신호방향으로 출력전력을 최소화하고 잡음전력을 고려하여 구할 수 있다^[6]. 이 방식은 원하는 신호의 도래각이 정확히 알려져 있지 않 다면, 위에서 언급한 바와 같이, 심한 성능 저하를 초래 할 수 있다. 이에 대처하기 위해, 예를 들어, 반복적으로 QCQP(quadratically constrained quadratic program- ming)문제의 해를 구하거나^[7,8] 두 부공간의 교집합을 이용하거나^[9], 여러 개의 불확실 집합에 기반하거나^[10], 확장조향벡터의 잡음 부공간에 대한 직교성을 이용하 여^[11] 오류에 강인한 확장조향벡터를 얻을 수 있다.

확장조향벡터 추정에 더해 간섭잡음 행렬을 구할 수 있다^{[7-9 ,11]}. 간섭잡음 행렬을 추정하여 원하는 신호의 영 향을 최소화하면 시스템 오류에 강인하고 빠르게 수렴 하는 장점을 가질 수 있다. 간섭 행렬을 구하기 위해 원하는 신호가 놓여 있는 공간각 섹터 Θ_d와, 이외 집합 [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$를 구분한다. 간섭행렬 추정을 위해 [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$ 영역에서 행렬적분을 하거나^[7,9], 간섭신호 방향을 추정하거나^[11], 간섭신호 방향을 추정하고 반복적으로 RCB(robust Capon beamforming)를 적용한다^[8]. 그러나 이들 방식 에서의 행렬적분, 반복계산, 비선형 문제의 해, 간섭신 호 방향 추정 등에 매우 많은 계산량이 요구되어 효율적 이지 못하다.

본 논문에서는, 비회전 계수가 1인 엄격한 비회전 신호가 수신될 때 간섭부공간을 추출하여 이 부공간에 직교하도록 가중벡터를 구하는 계산이 간편한 빔포밍 방법을 제시한다. 먼저, Θ_d 영역에서 MUSIC(multiple signal classification)^[12] 원리에 의거하여 원하는 신호 의 도래각과 비회전 계수를 추정하여 확장조향벡터를 구한다. 샘플행렬(sample matrix)로부터 신호행렬을 계 산하고 구한 확장조향벡터를 이용, 간섭 부공간을 추출 하여 가중벡터를 구한다. 확장수신벡터의 켤레 대칭성 을 이용하여 이의 계산 대부분이 실수영역에서 수행되 고, [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$ 영역에서는 어떤 계산도 하지 않아 간섭 행렬을 구성하거나 추정하는 방식에 비해 계산량이 매우 작다.

논문을 통해 사용하는 기호, 표기들은 다음과 같다. 위 첨자 T, *, H는 각각 전치(transpose), 켤레복소, 켤레 복소전치 연산, E[.]는 기대치 연산을, Re, Im은 복소수 의 실수부, 허수부를 나타낸다. 행렬, 벡터는 각각 대문 자, 소문자 굵은체로 나타내고, I는 적절한 크기의 단위 행렬이다. M개의 행을 가지는 행렬 Γ에 이의 복소 행 렬을 연결한 확장행렬을 [TeX:] $$\begin{equation} \Gamma^{\prime}\left(=\left[\Gamma^T, \Gamma^H\right]^T\right) \end{equation}$$으로 표현한 다. 2M개의 행을 가지는 임의의 행렬 Γ에서 처음 M행 을 Γ₁, 나머지 M행을 Γ₂로 표시한다. 즉, [TeX:] $$\begin{equation} \Gamma=\left[\Gamma_1^T, \Gamma_2^T\right]^T \end{equation}$$ 이다.

Ⅱ. 최적 WL 빔포머

M개의 센서로 구성된 선형 어레이에 원하는 신호와 K개의 간섭신호가 도래한다. 도래하는 전체신호의 수 는 [TeX:] $$$$이다. 도래각 θ에 대한 조향벡터를 a(θ) 로 나타낸다. 원하는 신호의 복소 포락선과 도래각은 s₀(t), θ₀, i번째 간섭신호의 복소 포락선과 도래각은 s_i(t), θ_i 이다. 전체 도래각 벡터는 [TeX:] $$\begin{equation} \boldsymbol{\theta}_I=\left[\theta_1, \cdots, \theta_K\right]^T \end{equation}$$는 간섭신호의 도래각 벡터로 이다. M × K₀ 조향벡터 행렬은

와 같이 나타낼 수 있다. 어레이에 수신된 신호는 다음 처럼 쓸 수 있다.

여기서 n(t)는 잡음벡터, s_I(t)는 간섭신호의 복소 포 락선 벡터로 [TeX:] $$\begin{equation} \boldsymbol{s}_I(t)=\left[s_1(t), \cdots, s_K(t)\right]^T \end{equation}$$이다.

도래하는 신호의 비회전 계수 [TeX:] $$\begin{equation} \gamma_i(i=0,1, \cdots, K) \end{equation}$$는 [TeX:] $$\begin{equation} \gamma_i=E\left[s_i^2(t)\right] / p_i \end{equation}$$와 같이 정의되고, 여기서 [TeX:] $$\begin{equation} p_i=E\left[s_i(t) s_i^*(t)\right] \end{equation}$$이다 . 이들 신호는 엄격한 비회전 신 호로 [TeX:] $$\begin{equation} \left|\gamma_i\right|=1 \end{equation}$$이다. 초기위상은 [TeX:] $$\begin{equation} \phi=\left[\phi_0, \phi_I^T\right]^T, \end{equation}$$ [TeX:] $$\begin{equation} \phi_I=\left[\phi_1, \cdots, \phi_K\right]^T \end{equation}$$이고, 이때 s(t)는

와 같이 표현할 수 있고

이며, ξ(t)는 실수 벡터이다. 원하는 신호는 간섭신호 와 상관되어 있지 않다 . 즉, [TeX:] $$\begin{equation} E\left[\xi_0(t) \boldsymbol{\xi}_I(t)\right]=\mathbf{0} \end{equation}$$이다 . 잡 음은 회전 복소 가우시안 프로세스(circular complex Gaussian process)로 센서 간에 서로 상관되어 있지 않 다. 다시 말하면, [TeX:] $$\begin{equation} E\left[\boldsymbol{n}(t) \boldsymbol{n}^H(t)\right]=\sigma^2 I \end{equation}$$, [TeX:] $$\begin{equation} E\left[\boldsymbol{n}(t) \boldsymbol{n}^T(t)\right]=\mathbf{0} \end{equation}$$이고, σ²은 잡음전력이다.

WL 방식에서는 x(t)와 이의 켤레복소를 연결한 확 장수신벡터 x'(t)를 이용하여 어레이 출력을 얻는다. 식 (2) – (5)로부터

와 같이 쓸 수 있고, [TeX:] $$\begin{equation} A(\theta, \phi) \end{equation}$$는 확장조향벡터 행렬로

이다. 원하는 신호는 간섭신호와 상관되어 있지 않아 x'(t)에 대한 공분산 행렬은

와 같이 쓸 수 있고, [TeX:] $$\begin{equation} \boldsymbol{R}_{\boldsymbol{\xi}_I}=E\left[\boldsymbol{\xi}_I(t) \boldsymbol{\xi}_I^H(t)\right] \end{equation}$$ [TeX:] $$\begin{equation} \boldsymbol{R}_{\boldsymbol{\xi}}=E\left[\boldsymbol{\xi}(t) \boldsymbol{\xi}^H(t)\right] \end{equation}$$ 이다.

어레이 출력신호 z(t)는

와 같이 주어지고, [TeX:] $$\begin{equation} \boldsymbol{w}=\left[\begin{array}{lll} w_1, & \cdots, & w_{2 M} \end{array}\right]^T \end{equation}$$는 가중벡터 이다. 어레이 출력전력 p_out은

와 같이 나타내진다 . 확장조향벡터 [TeX:] $$\begin{equation} a\left(\theta_0, \phi_0\right) \end{equation}$$를 a₀로 간 략히 표시한다. WL-MVDR에서는 원하는 신호 방향에 대한 빔 크기를 단위이득으로 제한하면서 출력전력 p_out이 최소가 되도록 가중벡터를 설정한다.

식 (12)의 최소화 문제의 해를 구하면

와 같고 , 상수 &mu는 (12b)에 따라 [TeX:] $$\begin{equation} \mu=1 / a_0^H R_{x^{\prime}}^{-1} a_0 \end{equation}$$으로 주어진다. 최적 가중벡터 w_o는 어레이 출력에서 SINR 을 최대로 한다.

Ⅲ. 제안 빔포밍 방식

3.1 간섭 부공간 추출

먼저, 간섭 부공간 추출과 관련하여 제안방식의 이론 적 근거를 설명한다. 공분산 행렬 R_x'은 다음처럼 고유 분해할 수 있다.

여기서 λ_m, e_m은 고유치, 고유벡터 쌍이고, 고유치는 내림차순으로 정렬되어 [TeX:] $$\begin{equation} \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_{2 M} \end{equation}$$이다. Λ_s 은 K₀ × K₀ 대각행렬로 대각요소는 σ²보다 큰 고유 치로 구성되고 E_s은 대응하는 고유벡터 행렬이다. 대 각행렬 λ_n의 대각요소는 σ²으로 같고 E_n은 대응하는 고유벡터 행렬이다. 고유분해로부터 신호행렬 [TeX:] $$\begin{equation} G \equiv A(\theta, \phi) R_{\xi} A(\theta, \phi)^H \end{equation}$$를

와 같이 구할 수 있다. 신호행렬 G에서 원하는 신호 성분을 제거하면 간섭 부공간을 얻을 수 있다. 행렬 λ 의 열공간에 직교하는 투사행렬을 [TeX:] $$\begin{equation} P_{\Gamma}^{\perp} \end{equation}$$와 같이 나타낸다. 원하는 신호의 확장조향벡터에 직교하는 투사행렬은

와 같이 주어진다. 식 (9)로부터, 신호행렬 G는

와 같이 쓸 수 있고 G에 [TeX:] $$\begin{equation} P_{a_0}^{\perp} \end{equation}$$를곱하면

와 같이 주어진다. G_I를 SVD(singular value decom- position)하여

와 같이 나타낼 수 있다. 특이값은 크기 순으로 정렬되 어 있고 행렬 G_I의 랭크는 K이다. 다시 말하면, 앞에서 K개만 0보다 큰 값을 가지고 있고 나머지는 모두 0인 값을 가진다. U_I,K는 좌 특이벡터 U_I의 처음 K 열로 구성되는 행렬이다. U_I,K의 열벡터는 간섭 부공간을 생 성한다.

3.2 빔포밍 알고리즘

실제의경우, R_x'는 알려져 있지 않고 데이터 샘플 로부터 추정해야 한다. N개의 데이터 샘플이 있다면 R_x'을

과 같이 추정할 수 있다. 켤레 대칭성을 갖는 2M × 1 벡터는 아래 식(22)와 같이 정의되는 2M × 2M 유니 터리(unitary) 행렬 Π를 이용해서 실수벡터로 변환할 수 있다^[11].

x'(t)에 Π의 켤레전치를 곱하면

와 같고 x'(t)는 실수벡터 y(t)로 변환된다. y(t)에 대한 샘플행렬은

과 같이 주어진다^[11].

실수행렬 [TeX:] $$\begin{equation} \widehat{\boldsymbol{R}}_y \end{equation}$$를 고유분해하여

와 같이 나타낼 수 있다. 식 (23)에 따라 [TeX:] $$\begin{equation} \widehat{\boldsymbol{R}}_{x'} \end{equation}$$는

와 같다. 따라서 [TeX:] $$\begin{equation} \hat{\Lambda}=\hat{\Lambda}_y, \hat{E}=\Pi \hat{E}_y \end{equation}$$이고

임을 쉽게 알 수 있다. [TeX:] $$\begin{equation} \widehat{E}_1 \end{equation}$$, [TeX:] $$\begin{equation} \widehat{E}_2 \end{equation}$$는,앞에서정의한대로, 2M개의 행을 갖는 [TeX:] $$\begin{equation} \widehat{E} \end{equation}$$의 처음 M행, 나머지 M행을 나 타낸다.

3.2.1 확장조향벡터 계산

NC-MUSIC(noncircular MUSIC)에 따라 비회전 신 호의 도래각을 추정할 수 있다. NC-MUSIC에서 목적 함수 f(θ)는

와 같다^[11,12]. 여기서 [TeX:] $$\begin{equation} \widehat{E}_n \end{equation}$$은 [TeX:] $$\begin{equation} \widehat{R}_x \end{equation}$$의 잡음 고유벡터행렬로 [TeX:] $$\begin{equation} \widehat{E} \end{equation}$$에서 뒤로부터 (2M - K₀)열로 구성되고 [TeX:] $$\begin{equation} \widehat{E}_{n1} \end{equation}$$은 [TeX:] $$\begin{equation} \widehat{E}_n \end{equation}$$ 의 처음 M행으로 구성되는 행렬이다. 원하는 신호의 도래각 영역이

와 같이 주어졌다고 하자. θ₀₀는 θ₀의 초기 추정값, Δθ 는 사전에 정해진 상수이다. 도래각 θ₀의 추정은

와 같이, 위상 φ₀의 추정은

와 같이 구해진다^[11,12]. [TeX:] $$\begin{equation} \hat{\theta}_0, \hat{\phi}_0 \end{equation}$$를 구하면 [TeX:] $$\begin{equation} \hat{a}_0 \end{equation}$$은

처럼 계산된다.

3.2.2 가중벡터 계산

샘플행렬의 고유분해로부터 신호행렬은

처럼 쓸 수 있다. 여기서

이고, [TeX:] $$\begin{equation} \widehat{E}_{y s} \end{equation}$$는 [TeX:] $$\begin{equation} \widehat{E}_{y} \end{equation}$$의 처음 K₀ 열로 [TeX:] $$\begin{equation} \widehat{E}_{y n} \end{equation}$$구성된다. 잡음전력은

와 같이 추정된다. [TeX:] $$\begin{equation} \hat{a}_0 \end{equation}$$에 직교하는 투사행렬 [TeX:] $$\begin{equation} P_{\hat{a}_0}^{\perp} \end{equation}$$은

와 같이 나타낼 수 있다. G_I 의 추정은 (36), (40)으로 부터

와 같이 표현된다. 식 (42)에 따라 [TeX:] $$\begin{equation} \widehat{G}_{I} \end{equation}$$의 특이벡터는 [TeX:] $$\begin{equation} \widehat{G}_{y I} \end{equation}$$의 특이벡터에 유니터리 행렬 Π를 곱하면 구해진 다. 실수행렬 [TeX:] $$\begin{equation} \widehat{G}_{y I} \end{equation}$$를 SVD하여 앞에 있는 K개의 좌 특 이벡터로 실수행렬 [TeX:] $$\begin{equation} \widehat{U}_{y I, K} \end{equation}$$를 얻고, 간섭 부공간은

와 같이 주어진다. 식 (44)에 따라 [TeX:] $$\begin{equation} \widehat{U}_{I, K} \end{equation}$$의 열공간에 직 교하는 투사행렬은 다음처럼 표현할 수 있다.

[TeX:] $$\begin{equation} \widehat{U}_{I, K} \end{equation}$$를 구하면, 가중벡터를

와 같이 구할 수 있고, w_y1, w_y2는 각각 w_y의 처음 M 요소, 마지막 M 요소로 구성되는 벡터이다. 상수 μ는 [TeX:] $$\begin{equation} w^H \hat{\boldsymbol{a}}_0=w_y^H \hat{\boldsymbol{a}}_{y 0}=1 \end{equation}$$의 제한조건에 따라 계산할 수 있다. 식 (46)에서 보듯이 w는 켤래 대칭성을 가진다. 표 1에 제안방식의 가중벡터를 구하는 과정을 요약하였 다. 벡터 w_y는 실수벡터이다. w_y는 실수행렬 [TeX:] $$\begin{equation} \widehat{R}_y \end{equation}$$로부 터 실수영역에서 [TeX:] $$\begin{equation} \widehat{G}_y \cdot \widehat{G}_{y I}, \widehat{U}_{y I, K} \end{equation}$$를 계산하여 구해진다. w_y를 구하면 식 (46)에 따라 가중벡터를 얻는다.

3.3 복잡도

설명한 바와 같이, 제안방식의 계산과정 대부분은 실 수영역에서 이루어지고 w_y가 실수영역에서 구해진다. 편의상 M' = 2M으로 나타낸다. 표 2에 실수곱셈 측면 에서 제안방식의 계산량을 요약하였다. EVD(ei- genvalue decomposition)는 고유분해를 의미한다. [TeX:] $$\begin{equation} \hat{R}_y \end{equation}$$ 계산에 O(NM'²⁾, [TeX:] $$\begin{equation} \hat{R}_y \end{equation}$$의 고유분해와 [TeX:] $$\begin{equation} \hat{G}_y \end{equation}$$의 SVD에 O(M'³)의 실수곱셈 계산량이 요구된다. 식(31)의 a(θ)는(26),(27)로부터

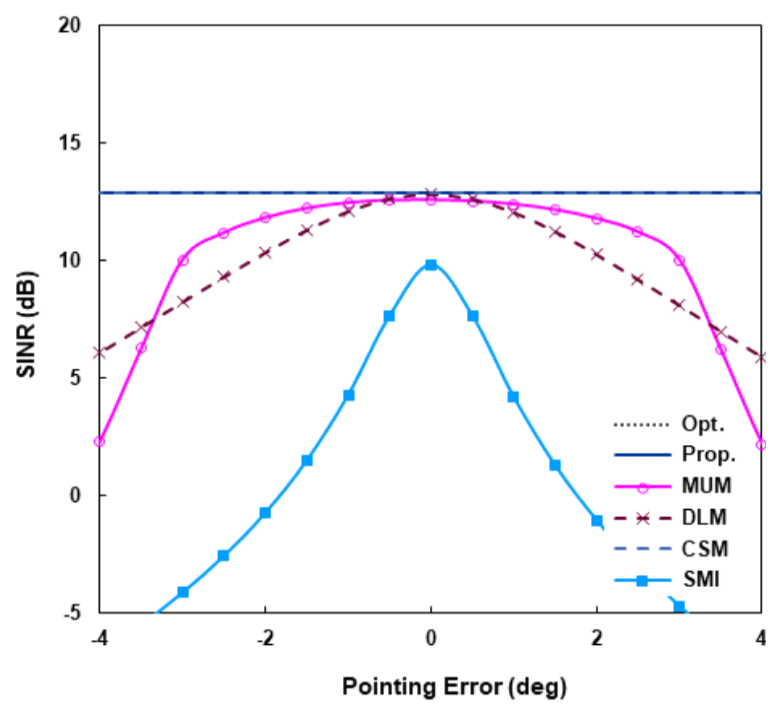
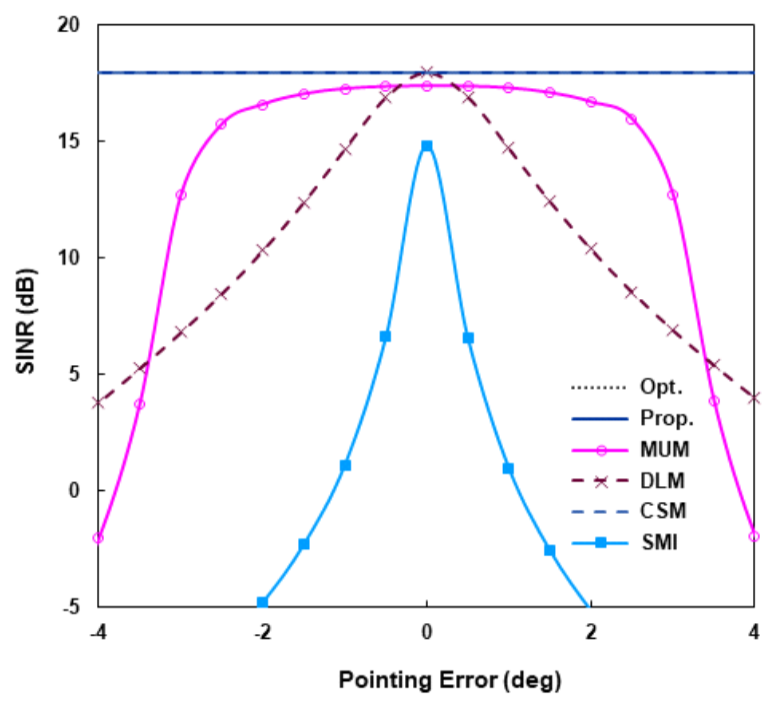
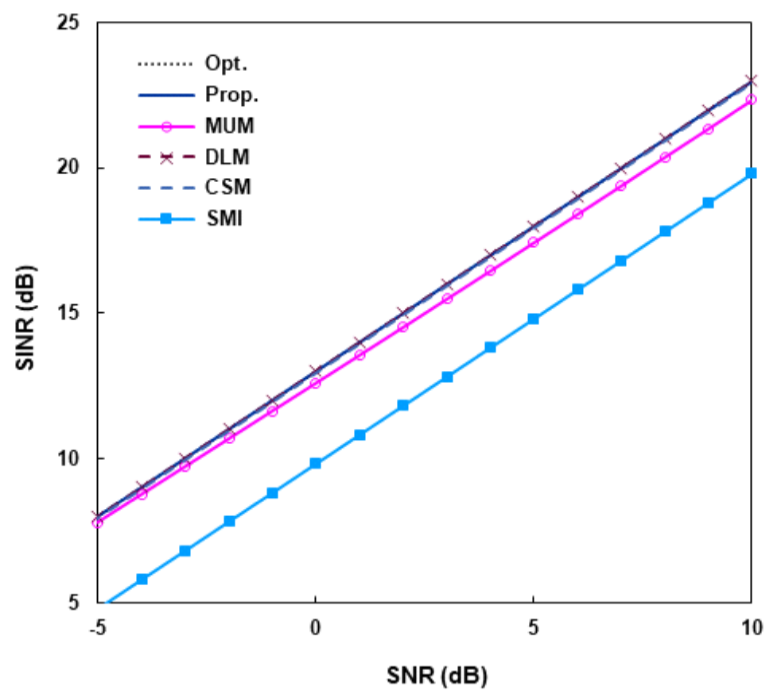
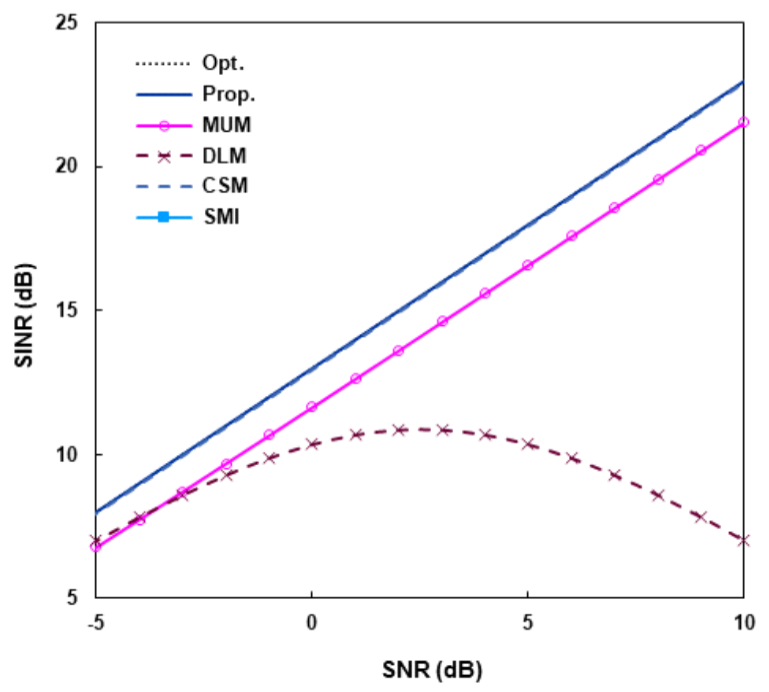
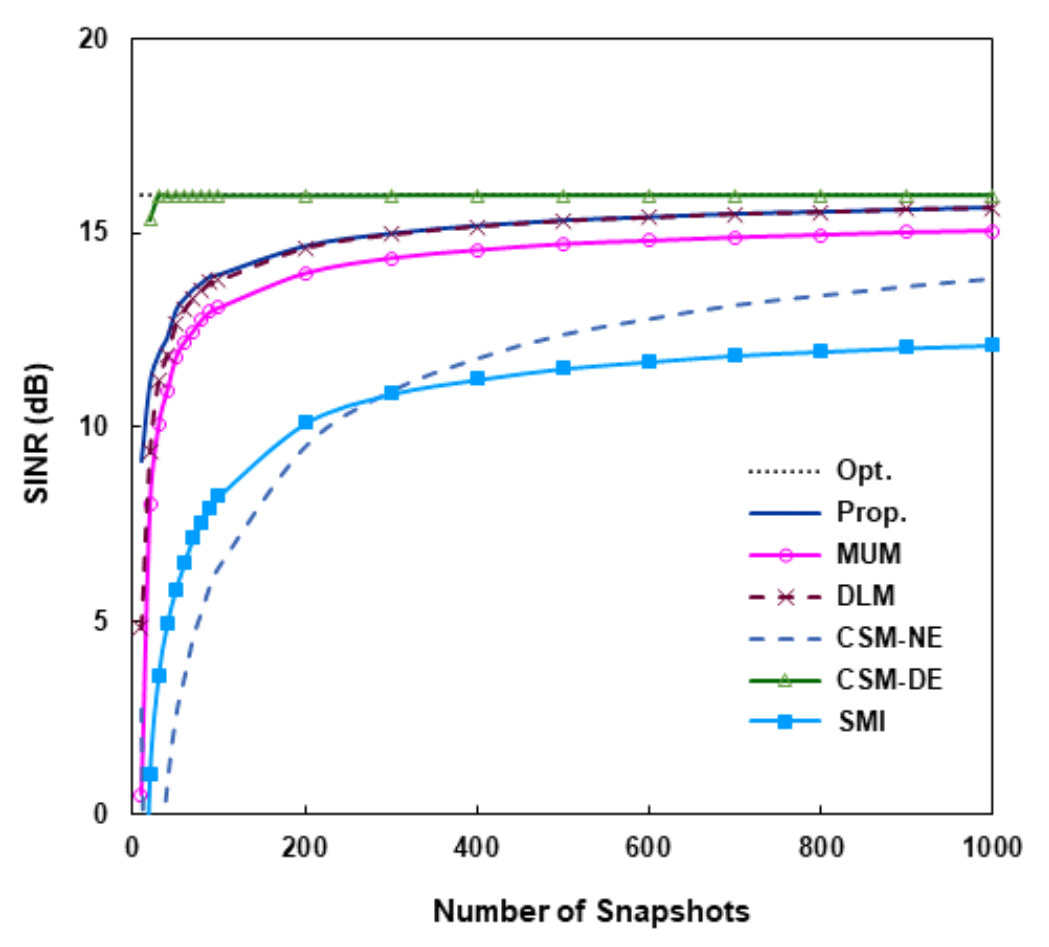
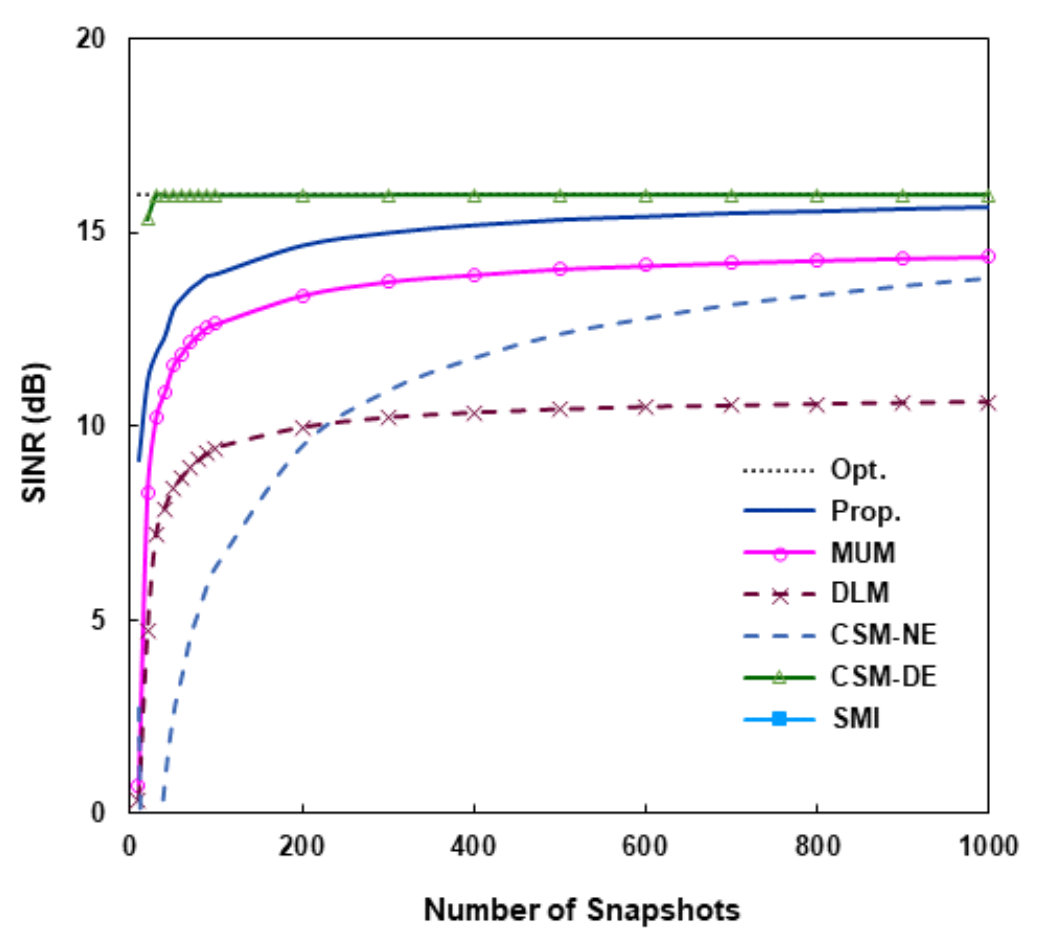
와 같이 주어진다. α(θ)에 [TeX:] $$\begin{equation} O\left(M^{\prime 2}\right) \end{equation}$$ 계산이 요구되어 [TeX:] $$\begin{equation} \hat{\theta}_0, \hat{\phi}_0 \end{equation}$$에 [TeX:] $$\begin{equation} O\left(N_d M^{\prime 2}\right) \end{equation}$$ 실수곱셈 계산량이 필요하고, N_d 는 Θ_d 영역에서 탐색점의 개수이다. 전체적으로 제안 방식의 복잡도는 실수곱셈의 견지에서 [TeX:] $$\begin{equation} O\left(N M^{\prime 2}+N_d M^{\prime 2}+M^{\prime 3}\right) \end{equation}$$이다.

참고문헌 [11]의 CSM(conjugate symmetry meth- od)방식에서 원하는 신호에 대한 확장조향벡터를 구하 는 과정은 제안방식과 동일하다. CSM에서는 NC-MUSIC을 통해 [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$ 영역에서도 탐색을 하여 간섭 신호의 도래각을 추정하고 간섭전력을 계산하여 간섭 잡음 행렬을 구한다. 그리고 이 행렬의 역행렬을 계산해 서 가중벡터를 구한다. 실수행렬 [TeX:] $$\begin{equation} \widehat{R}_y \end{equation}$$를 고유분해하고 [TeX:] $$\begin{equation} \hat{\theta}_0, \hat{\phi}_0 \end{equation}$$을 구한 다음, 추가적으로 간섭신호의 도래각, 간섭잡음 행렬의 역행렬을 구해야 하는데, 이에 [TeX:] $$\begin{equation} O\left(N_I M^{\prime 2}+M^{\prime 3}\right) \end{equation}$$ 계산량이 요구되고, N₁는 [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$ 영역 에서 탐색점의 개수이다. 제안방식과 비교하면 CSM의 계산량이 [TeX:] $$\begin{equation} O\left(N_I M^{\prime 2}\right) \end{equation}$$만큼 많다. 정확한 도래각 추정을 위해서는 많은 탐색점이 요구되어 [TeX:] $$\begin{equation} N_I \gg M \end{equation}$$ 이고 [TeX:] $$\begin{equation} N_I \gg N_d \end{equation}$$ 이므로, 제안방식은 CSM보다 매우 작은 계 산량을 가진다.

Ⅳ. 시뮬레이션

10개로 구성된 ULA(uniform linear array)에 3개의 신호가 수신된다. 센서는 반파장 간격으로 놓여 있고 원하는 신호는 [TeX:] $$\begin{equation} \theta_0=0^{\circ} \end{equation}$$로부터, 두 간섭신호는 [TeX:] $$\begin{equation} \theta_1=-25^{\circ} \end{equation}$$, [TeX:] $$\begin{equation} \theta_2=15^{\circ} \end{equation}$$로부터 입사한다. 간섭신호의 전 력은 서로 같고, 원하는 신호보다 10dB 크다. 제안방식 의 SINR 성능을 MUM(multiple uncertainty set meth- od)^[10], DLM(diagonal loading method)^{[ 6]}, CSM^[11]의 WL 방식과 표준 SMI(sample matrix inversion)^[1] 방식 과 비교한다. 식 (32)의 Θ_d에서 [TeX:] $$\begin{equation} \Delta \theta=5^{\circ} \end{equation}$$이다. MUM에 서 여러 개의 파라미터 설정이 필요한데, 불확실 집합 (uncertainty set)의 수는 3, 각 집합의 크기(참고문헌 [10]에서 [TeX:] $$\begin{equation} \tilde{\epsilon}_l(l=1, \cdots, 3) \end{equation}$$로 표기됨)는 0.7, 각 중심과 관련된 제한점은 2° 간격으로 [TeX:] $$\begin{equation} \left(\theta_{00}-2^{\circ}\right) \end{equation}$$, θ₀₀, [TeX:] $$\begin{equation} \left(\theta_{00}+2^{\circ}\right) \end{equation}$$이다. DLM에서 [TeX:] $$\begin{equation} 10 \hat{\sigma}^2 \end{equation}$$의 로딩 값을 사용하였 다. 그림 1-4는 스냅샷의 개수 N이 무한개인 정상상태 (steady state)에서 R_x'을 이용한 성능을, 그림 5, 6은 샘플행렬을 이용한 N의 함수로 평균 SINR을 나타낸 다. 100 번의 모의실험을 통해 평균값을 구하였다.

그림 1, 2는 포인팅 오류 [TeX:] $$\begin{equation} \theta_e\left(=\theta_{00}-\theta_0\right) \end{equation}$$에 대한 SINR을 보여준다. 그림 1에서 입력 SNR(signal-to- noise ratio)은 0 dB, 그림 2에서는 5 dB이다. R_x'을 이용하면 제안방식은 원하는 신호의 도래각과 비회전 계수를 정확히 구할 수 있다. 그림에서, 제안방식 , CSM 성능은 최적 성능과 중첩되어 있고, 실질적으로 동일한 성능을 보인다. 반면에 MUM, DLM은 오류가 증가함 에 따라 큰 성능저하를 보인다. 그림 1, 2를 비교하면, 이러한 저하는 SNR이 커지면 심해짐을 알 수 있다. MUM은 오류가 작으면 작은 성능저하를 보이지만, 그 림 1에서 대략 [TeX:] $$\begin{equation} \left|\theta_e\right|>3^{\circ} \end{equation}$$, 그림 2에서 [TeX:] $$\begin{equation} \left|\theta_e\right|>2.5^{\circ} \end{equation}$$ 이면 SINR이 급격하게 감소한다.

그림 3, 4는 SNR에 따른 성능을 비교한다. 그림 3에 선 포인팅 오류가 없고, 즉, [TeX:] $$\begin{equation} \theta_e=0^{\circ} \end{equation}$$이고, 그림 4에서는 [TeX:] $$\begin{equation} \theta_e=2^{\circ} \end{equation}$$이다. 최적성능, 제안방식, CSM의 SINR은 중 첩되어 있다. 그림 4에서의 DLM, SMI 성능을 제외하 고 두 그림 모두에서 각 SINR은 SNR에 선형적으로 증가함을 보인다. 그림 3에서 보듯이 오류가 없으면. DLM은 실질적으로 최적성능을 보이고, MUM은 SNR 이 증가함에 따라 최적성능과의 차가 조금 커진다. WL 방식을 사용하지 않는 SMI는 최적성능과 약 3dB 차이 를 보인다. 오류가 있는 그림 4의 경우, SMI의 SINR은 1dB 보다 작은 값을 보인다. DLM은 SNR이 매우 작으 면 SNR에 따라 선형적으로 증가하지만 어떤 값보다 크면 원하는 신호 방향으로 깊은 널을 형성하여 오히려 SINR이 감소한다.

샘플행렬을 이용할 때, 그림 5, 6에서는 스냅샷의 개 수 N에 대한 성능을 나타낸다. 각각 [TeX:] $$\begin{equation} \theta_e=0, \theta_e=2^{\circ} \end{equation}$$이 고, SNR은 모두 3dB이다. CSM의 경우, 간섭신호의 도래각도 추정하여 간섭잡음 행렬을 구하는 CSM-DE(direction estimation)와 그렇지 않은 CSM-NE(no estimation)의 성능을 함께 제시하였다. CSM-NE의 경우, 원하는 신호에 대한 확장조향벡터의 추정은 제안방식과 동일하고 샘플행렬의 역행렬을 구 해 가중벡터를 구한다. 그림 6에서 SMI의 SINR은 –3 dB보다 작다. 그림 5, 6에서 각 방식은 N이 증가함에 따라 각각 그림 3, 4에 보인 정상상태 SINR에 접근한 다. CSM-DE는 매우 빠른 수렴 속도를 보여, 오류 유무 에 관계없이 [TeX:] $$\begin{equation} N \geq 30 \end{equation}$$ 이면 최적성능의 0.1dB 이내의 성능을 보인다. 제안방식도 오류에 관계없이 빠른 수렴 속도를 보이고, CSM-DE외 다른 방식보다 우수한 성능 을 나타낸다.

그림 6의 시뮬레이션에서 평균 실행시간을 구하였 다. 제안방식의 평균 실행시간을 1로 했을 때, N=200 에서 CSM-NE는 0.96, CSM-DE는 17.3, MUM은 162.7을 나타내었다. 다른 N에서도 CSM-DE, CSM-NE는 비슷한 값을 보였다. 그러나 MUM은 N이 증가함에 따라 다소 감소하는 경향를 보여 N=50에서 211.2, N=1000에서 149.8을 기록하였다. 예상한 대 로 제안방식은 CSM-NE와 비슷하고 CSM-DE보다는 훨씬 작은 실행시간을 가진다. MUM의 경우, SDP(semidefinite programing) 비선형 문제의 해를 구 하고 반복계산을 해야 함에 따라 많은 실행시간이 요구 된다.

Ⅴ. 결 론

엄격 비회전 신호가 도래할 때 효율적인 WL 빔포밍 방식을 제안하였다. 제안방식에서는 먼저, 실수행렬 [TeX:] $$\begin{equation} \widehat{R}_y \end{equation}$$ 를 고유분해하여 Θ^d 영역에서 NC-MUSIC에 의거해 서 원하는 신호의 도래각과 초기위상을 추정하여 확장 조향벡터를 구한다. [TeX:] $$\begin{equation} \widehat{R}_y \end{equation}$$의 고유분해로부터 식 (38), (43) 처럼 [TeX:] $$\begin{equation} \widehat{G}_y, \widehat{G}_{y I} \end{equation}$$를 구하고 [TeX:] $$\begin{equation} \widehat{G}_{y I} \end{equation}$$를 SVD하여 [TeX:] $$\begin{equation} \widehat{U}_{y I, K} \end{equation}$$를 얻는 다. [TeX:] $$\begin{equation} \widehat{U}_{y I, K} \end{equation}$$를 이용하여 가중벡터는 간섭 부공간에 직교 하도록 식 (46)과 같이 계산된다. 제안방식에서는 계산 과정이 거의 대부분 실수 영역에서 효율적으로 이루어 진다. 이에 따라, 예를 들어, 비선형 문제의 해를 반복적 으로 구해야 하는 MUM보다 계산량이 훨씬 작다.

시뮬레이션 결과에 따르면, 제안방식은 포인팅 오류 에 강인한 특성을 보이면서 MUM, CSM-NE 등 다른 WL 빔포머보다 우수한 성능을 나타낸다. 그러나. 매우 빠르게 최적 성능에 접근하는 CSM-DE보다는 다소 늦 은 수렴속도를 보인다. 그렇지만, CSM-DE는 [TeX:] $$\begin{equation} \bar{\Theta}_d \end{equation}$$ 영역 에서 간섭신호의 도래각과 전력을 추정해야 해서 제안 방식보다 계산량이 훨씬 크다. 확장수신벡터 x'(t)는 식 (6)에서 보듯이, ULA 어레이가 아니더라도 그 구성 자체로 켤레 대칭성을 가진다. 제안 방식은 임의의 선형 어레이에 적용할 수 있다.