Impact of Beam Split and IQ Mismatch on BER Performance of IRS-aided THz Communications

Ⅰ. Introduction

Terahertz (THz) communication is considered a promising technology for the next-generation wireless networks due to viability of large bandwidth. THz communication can support the ultra-high data rate with ultra-massive connectivity in a wireless network for various applications such as holographic commu- nication, immersive virtual reality, and digital twins. As compared to millimeter Wave (mmWave) (30-100 GHz) for 5G, THz band (0.1-10 THz) can support the 10 GHz or even more channel bandwidth for data transmission. However, the transmission of THz sig- nals is significantly hindered by substantial prop- agation attenuation resulting from exceedingly high carrier frequencies^[1].

In the THz communication, maintaining a line-of-sight (LoS) path is essential for successful data transmission. If the LoS path is blocked or severely faded, reliable communication becomes impossible in THz bands. Recently, intelligent reflecting surfaces (IRS) have been introduced to create virtual LoS paths in the network or manipulate the channel between the transmitter (Tx) and receiver (Rx) in the THz communication. Furthermore, IRS has the capability to create additional signal propagation paths, effec- tively resolving blockage issues through proactive ma- nipulation of the wireless environment. Therefore, lev- eraging IRS in the THz communication presents an attractive prospect for the advancement of future 6G wireless systems. Similarly, massive multiple-input multiple-output (MIMO), which employs a large an- tenna array to produce directional beams with high array gains, offers a solution to mitigate the consid- erable signal attenuation inherent in THz communications. Thus, the THz massive MIMO holds significant promise for future next-generation wireless communications. In the THz communication, a sub- stantial number of antennas at the Tx and a consid- erable number of elements at the IRS are utilized to generate highly directional and energy-focused beams. This strategy aims to counteract the significant signal propagation attenuation experienced in THz communications.

In IRS-aided MIMO THz (IMT) communication, the integration of extensive bandwidth, numerous IRS elements, and massive antennas leads to significant beam splitting. As a result, the conventional phase-shifter-based hybrid precoding architecture be- comes ineffective. Recently, a delay-phase (DP) pre- coding (frequency-dependent) architecture has been proposed to alleviate the impact of beam splitting in IMT communication ^[4].

Contributions: This paper investigates the bit error rate (BER) performance of the IMT communication. We compare various DP precoding techniques for the IMT communication. Our observations indicate that double beam splitting (at IRS and Tx) can sig- nificantly reduce the BER performance of IMT communication. We analyze the impact of the number of IRS elements, Tx antennas, sub-carriers, IQ mis- match, and IRS location on BER. In addition, the ef- fect of imperfect channel state information (CSI) with and without IQ mismatch is also analyzed. The pre- sented results suggest that the large bandwidth of THz exacerbates the beam splitting effect and degrades the BER performance significantly.

Related Works: IRS-aided MIMO THz systems are analyzed in the literature ^[2-4]. Researchers are focusing on BER analysis ^[5], sumrate ^{[2,3, 6]}, signal detection ^{[7,8 ]}, beam split effect^[9,10], IRS-aided design ^[9,10],, coverage analysis^[8], outage probability (OP), and channel mod- eling ^[7] in the THz communication. While beam split effects are commonly analyzed for sumrate analysis in the literature, their impact on BER analysis in IMT system design is not considered or has received less attention. A summary of works related to beam split effects is provided in Table 1.

Ⅱ. IMT System Model

The transmitter is equipped with transmit antennas, incorporating both a time-delay (TD) network and phase shifts (PS). Modulated data undergoes precod- ing by a digital precoder before being transmitted through the radio-frequency (RF) chains, as depicted in Fig. 1. The IRS panel comprises elements arranged horizontally and vertically. The direct LoS between Tx and Rx is obstructed due to severe fading or ob- stacles, with a virtual LoS established between them via the IRS. To mitigate the effect of beam splitting in the IMT communication, frequency-dependent pre- coding is implemented at the Tx, while DP shifting is applied at the IRS panel. Rx employs maximum likelihood signal detection and is equipped with a sin- gle antenna.

The commonly employed orthogonal frequency di- vision multiplexing (OFDM) scheme with Msub-car- riers is considered. The received downlink signal, de- noted as y_m at the m-th sub-carrier (m=1,… ,M ), can be expressed as

The expression [TeX:] $$\begin{equation} \mathbf{w} x_m \in \mathbb{C}^{N_{\mathrm{t}} \times 1} \end{equation}$$ signifies the trans- mitted signal at the Tx. Here, [TeX:] $$\begin{equation} x_m \in \mathbb{C} \end{equation}$$ denotes the transmitted information symbol at the m-th sub-car- rier, ensuring unit energy, i.e., [TeX:] $$\begin{equation} \mathrm{E}\left[\left|\mathrm{x}_{\mathrm{m}}\right|^2\right]=1 \end{equation}$$, while [TeX:] $$\begin{equation} \mathbf{w} \in \mathbb{C}^{N_{\mathrm{t}} \times 1} \end{equation}$$ represents the precoding vector. Additionally, n_m represents the additive white Gaussian noise (AWGN) with zero mean and variance σ². The matrix [TeX:] $$\begin{equation} \mathbf{G}_m \in \mathbb{C}^{N \times N \mathrm{t}} \end{equation}$$ represents the Tx-RIS channel response. The vector [TeX:] $$\begin{equation} \mathbf{h}_m^{\mathrm{T}}=\left[h_{m, 1}, h_{m, 2}, \ldots, h_{m, N}\right] \in \mathbb{C}^{1 \times N} \end{equation}$$ denotes the channel from the IRS to the Rx at the m -th sub-carrier.

The response of each IRS element to the incident signal is expressed as [TeX:] $$\begin{equation} a_n e^{j \theta}, n=1,2, \ldots, N \end{equation}$$, where θ_n is the phase and an denotes the reflection coefficient. Thus, the overall IRS panel response can be written as

The IRS matrix is denoted as [TeX:] $$\begin{equation} \boldsymbol{\Theta}=\operatorname{diag}[\boldsymbol{\theta}] \end{equation}$$, where the expression [TeX:] $$\begin{equation} \operatorname{diag}[\theta] \end{equation}$$ represents a diagonal matrix constructed with elements selected from the vector θ.

The channel matrix G_m between Tx-IRS panel is

where τ₁ is the path delay from Tx to IRS. [TeX:] $$\begin{equation} j=\sqrt{-1} \end{equation}$$ is a complex number. The path gain [TeX:] $$\begin{equation} g_1\left(f_m, d_1\right) \in \mathbb{C} \end{equation}$$ is expressed as

where c denotes the speed of light, and d₁ is the dis- tance from the Tx to the IRS panel. [TeX:] $$\begin{equation} \tau_{\mathrm{abs}}\left(f_m\right) \end{equation}$$ is the molecular absorption coefficient at the m -th sub-carrier frequency f_m. The elevation angle and the azimuth angle of the angle-of-arrival (AoA) of the RIS panel are denoted as [TeX:] $$\begin{equation} \eta_1^r \end{equation}$$ and [TeX:] $$\begin{equation} \zeta_{1,}^r \end{equation}$$, respectively. The transmit angle of the Tx is denoted as φ. Furthermore, in the channel matrix, we assume that a LoS path exists between the Tx and the IRS panel.

The steering vector [TeX:] $$\begin{equation} \mathbf{a} \in \mathbb{C}^{N \times 1} \end{equation}$$ of IRS panel hav- ing uniform planar array (UPA) is expressed as

The steering vector [TeX:] $$\begin{equation} \mathbf{b}\left(f_m, \phi\right) \in \mathbb{C}^{N_{\mathrm{t}} \times 1} \end{equation}$$ of the uniform linear array (ULA) is expressed as

[TeX:] $$\begin{equation} \mathbf{b}\left(f_m, \phi\right)=\frac{1}{\sqrt{N_{\mathrm{t}}}}\left[1, e^{j 2 \pi \frac{f_m}{c} d \sin (\phi)}, \ldots, e^{j 2 \pi \frac{f_m}{c}\left(N_{\mathrm{t}}-1\right) d \sin (\phi)}\right]^{\mathrm{T}}. \end{equation}$$

Similarly, the channel vector h_m between IRS and Rx is expressed as

where τ₂ is the path delay from IRS to Rx. The path gain [TeX:] $$\begin{equation} g_2\left(f_m, d_2\right) \end{equation}$$ is expressed as

where d₂ is the distance from the IRS panel to the Rx. [TeX:] $$\begin{equation} \eta_2^t \end{equation}$$ and [TeX:] $$\begin{equation} \zeta_2^t \end{equation}$$ are the elevation angle and the azimuth angle of the angle-of-departure (AoD) at the IRS pan- el, respectively. These angles satisfy [TeX:] $$\begin{equation} \eta \in \mathbb{U}(0, \pi / 2) \end{equation}$$, [TeX:] $$\begin{equation} \zeta \in \mathbb{U}(-\pi, \pi) \end{equation}$$, and [TeX:] $$\begin{equation} \phi \in U(-\pi / 2, \pi / 2) \end{equation}$$, where [TeX:] $$\begin{equation} \mathbb{U}[a, b] \end{equation}$$ denotes the uniform distribution between a and b.

Ⅲ. Delay-phase Precoding at IRS

In the DP architecture, the frequency-dependent re- flection coefficient of the n-th IRS element is charac- terized by [TeX:] $$\begin{equation} e^{j\left(\theta_n-2 \pi f_m \tau_n\right)} \end{equation}$$, where τ_nrepresents the time delay. By appropriately adjusting the time delay of each element, the beams produced across various carriers can be synchronized with the desired target or physical direction. This synchronization effectively eradicates the beam split phenomenon in the IMT communication. Nonetheless, the utilization of TD modules typically entails significantly greater power consumption and hardware expenses when contrasted with systems employing solely phase shifters^{[5 ]}.

To mitigate high hardware complexity and power consumption, a sub-connected architecture for IRS is preferred. Each component within the sub-array is equipped with dual-layer phase shifters and is con- nected to a shared TD module via a circulator^{[2 ]}. Initially, the signal received at each component passes through the first-layer phase shifter, aiming to create constructive interference within the sub-array. Next, the signal is adjusted by the shared TD module. Finally, the signal passes through the second-layer phase shifter to complete the beamforming process of the IRS.

Let [TeX:] $$\begin{equation} Q_1 \times Q_2 \end{equation}$$ be the sub-arrays of an IRS panel, with each sub-array connected to a TD module. Each sub-array consists of [TeX:] $$\begin{equation} K_1 \times K_2 \end{equation}$$ elements, where [TeX:] $$\begin{equation} K_1=N_1 / Q_1 \end{equation}$$ and [TeX:] $$\begin{equation} K_2=N_2 / Q_2 \end{equation}$$. The index for ele- ments in each sub-array is denoted as [TeX:] $$\begin{equation} k=\left(k_1, k_2\right) \end{equation}$$, where [TeX:] $$\begin{equation} k_1=1,2, \ldots, K_1 \end{equation}$$ and [TeX:] $$\begin{equation} k_2=1,2, \ldots, K_2 \end{equation}$$. Each sub-array is identified by index [TeX:] $$\begin{equation} q=\left(q_1, q_2\right) \end{equation}$$, where [TeX:] $$\begin{equation} q_1=1,2, \ldots, Q_1 \end{equation}$$ and [TeX:] $$\begin{equation} q_2=1,2, \ldots, Q_2 \end{equation}$$.

Channel models are expressed as ^[2]

where the steering matrix F is expressed as

Here, [TeX:] $$\begin{equation} n_1=q_1 K_1+k_1 \end{equation}$$ and [TeX:] $$\begin{equation} n_2=q_2 K_2+k_2 \end{equation}$$. Phase shift matrices [TeX:] $$\begin{equation} (\Theta_1^q, \Theta_2^q) \end{equation}$$ representing the first and sec- ond layers, time delay vector P_m, and channel ma- trices [TeX:] $$\begin{equation} (\mathbf{G}_m^q, \mathbf{H}_m^q) \end{equation}$$ are generated for each sub-array. The received signal denoted by [TeX:] $$\begin{equation} y_m^q \end{equation}$$, after traversing from the transmitter, first-layer, and second-layer phase shifters of the IRS panel, can be formulated as^{[2, 10]}

where the TD vector P_m is

[TeX:] $$\begin{equation} \mathbf{p}_m=e^{-j 2 \pi f_m \mathbf{t}}, \quad \mathbf{t}=\left[t_1, t_2, \ldots, t_q, \ldots, t_{Q_1 \times Q_2}\right]^{\mathrm{T}} . \end{equation}$$

Ⅳ. Time-Delay Precoding at the Transmitter

Suppose the Tx is partitioned into P sub-arrays, each linked to a TD module. Let [TeX:] $$\begin{equation} t_{\mathrm{tx}} \in \mathbb{R} \end{equation}$$ represent the TD w_u,p and denotes the phase shift of the p-th sub-array (p = 1, ..., P) at the Tx. Consequently, the frequency-dependent transmit precoding of the Tx at the m-th sub-carrier can be described as

where blkdiag denotes the block diagonal matrix. Here W_u is defined as [TeX:] $$\begin{equation} W_u=\left[w_{u, 1}, w_{u, 2}, \ldots, w_{u, P}\right] \end{equation}$$. In addition, the elements of TD vector [TeX:] $$\begin{equation} \mathbf{p}_m^{\mathrm{tX}} \end{equation}$$ and the phase shifting matrix adhere to [TeX:] $$\begin{equation} t_p^{\mathrm{tx}}=\frac{(p-1)\left(\zeta_m-1\right) N_{\mathrm{t}} \sin (\phi)}{2 f_m P} \end{equation}$$ and [TeX:] $$\begin{equation} \left[\boldsymbol{w}_{u, 1}^{\mathrm{T}}, \ldots, \mathbf{w}_{u, P}^{\mathrm{T}}\right]^T=\mathbf{b}\left(f_m, \phi\right) . \end{equation}$$

Here [TeX:] $$\begin{equation} b(.) \end{equation}$$ denotes the steering vector of the ULA.

Ⅴ . Simulation Results

We analyze the average BER performance of the IMT communication system. Total system bandwidth is B Hz and sub-carriers are generated as

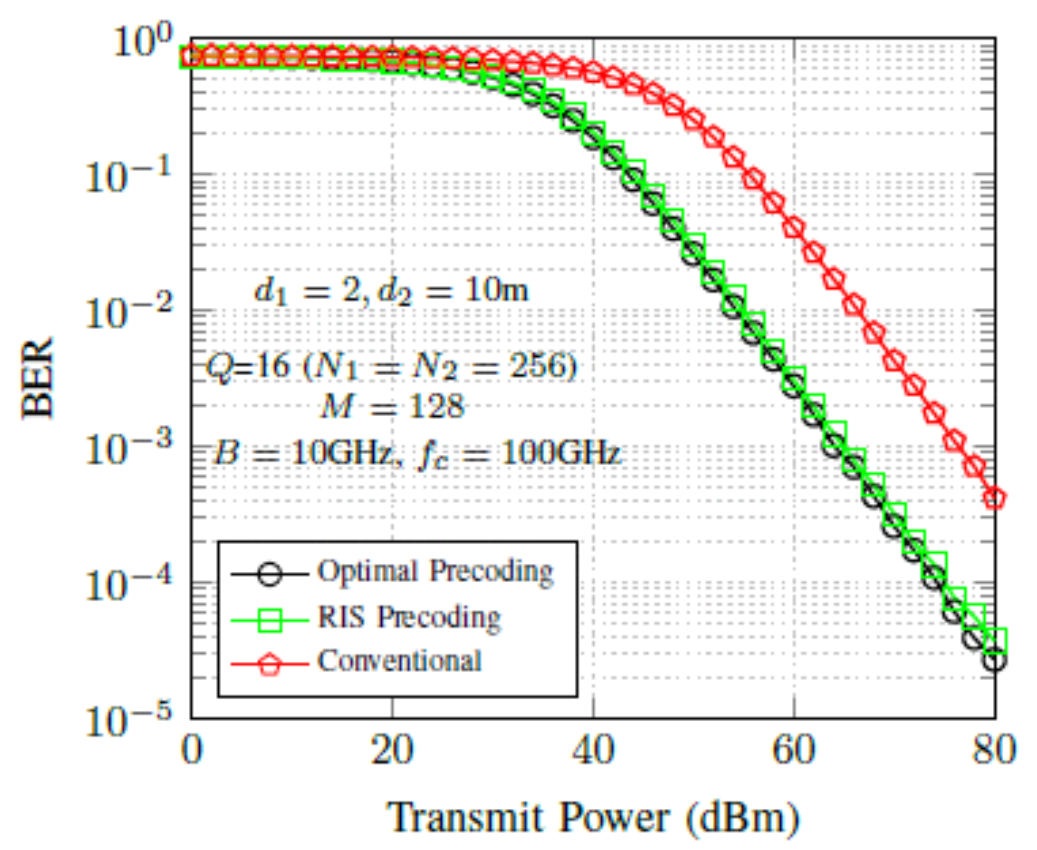
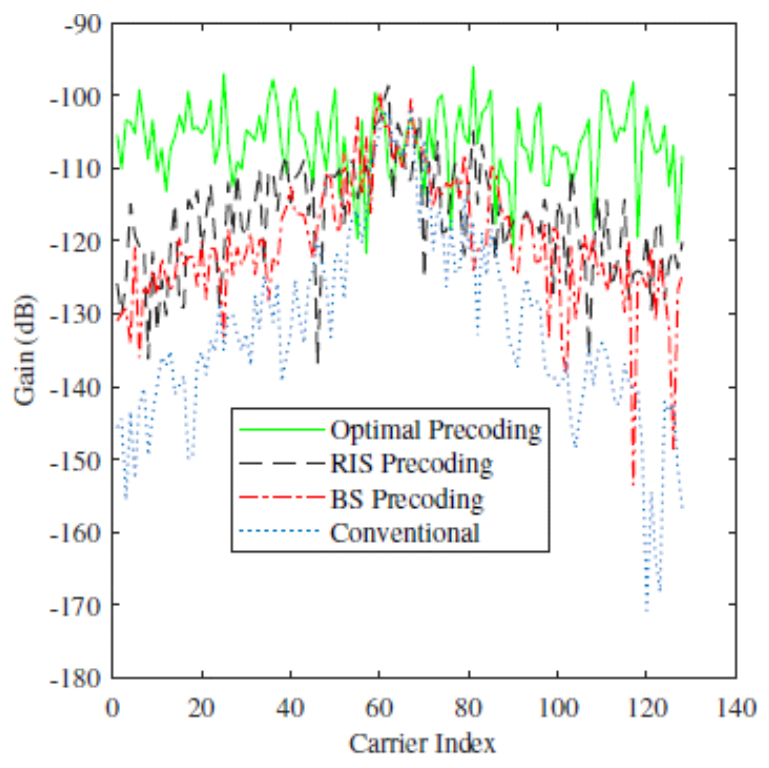
Here, f_c denotes the carrier frequency, and in simu- lations, we consider f_c = 100 GHz. The molecular ab- sorption coefficient is [TeX:] $$\begin{equation} \tau_{\mathrm{abs}}\left(f_m\right)=5.157 \times 10^{-4} \end{equation}$$ dB/m. The noise power is assumed to be [TeX:] $$\begin{equation} \sigma^2=-95 \end{equation}$$ dBm. The perfect knowledge of the channel state in- formation is assumed in simulations.

Fig. 2 illustrates the impact of beam split on BER performance at the IRS panel in the IMT system, con- sidering average gain per sub-carrier. The optimal pre- coding denotes that each element has a separate DP unit, while the IRS precoding denotes only one DP module attached to a sub-array of IRS elements. The conventional IRS design uses only frequency-in- dependent precoding by considering the center fre- quency only. The conventional IRS design exhibits degraded performance compared to the optimal and IRS precoding methods due to the beam split effect.

In Fig. 3, the average gain per sub-carrier of the IMT system is plotted for M=128. It can be observed that the gain of the conventional precoding scheme reduces as we move away from the center frequency of the beam due to the beam split effect. The optimal precoding demonstrates almost a similar gain for all the sub-carriers, as observed in Fig. 3, due to the DP precoding at the IRS and TD at the transmitter to com- pensate for the beam split phenomenon in the IMT. Only the IRS or the Tx exhibits improved gain com- pared to the conventional scheme, as the TD scheme is utilized either at the IRS or the Tx. Therefore, em- ploying the frequency-dependent precoding at both the Tx and IRS is essential in IMT.

The impact of the number of transmit antennas on BER performance is illustrated in Fig. 4, considering the average channel gain per sub-carrier. The optimal precoding exhibits the best performance due to the reduced beam split effect in the IMT system. The TD-based compensation is used in the optimal, RIS, and BS precoding methods. The beam split effect is higher for N_t=64, compared to N_t=16. Additionally, the impact of IRS elements on BER performance is illustrated in Fig. 5, considering N_t=256. The number of TD modules significantly affects the system per- formance, as observed in Fig. 5.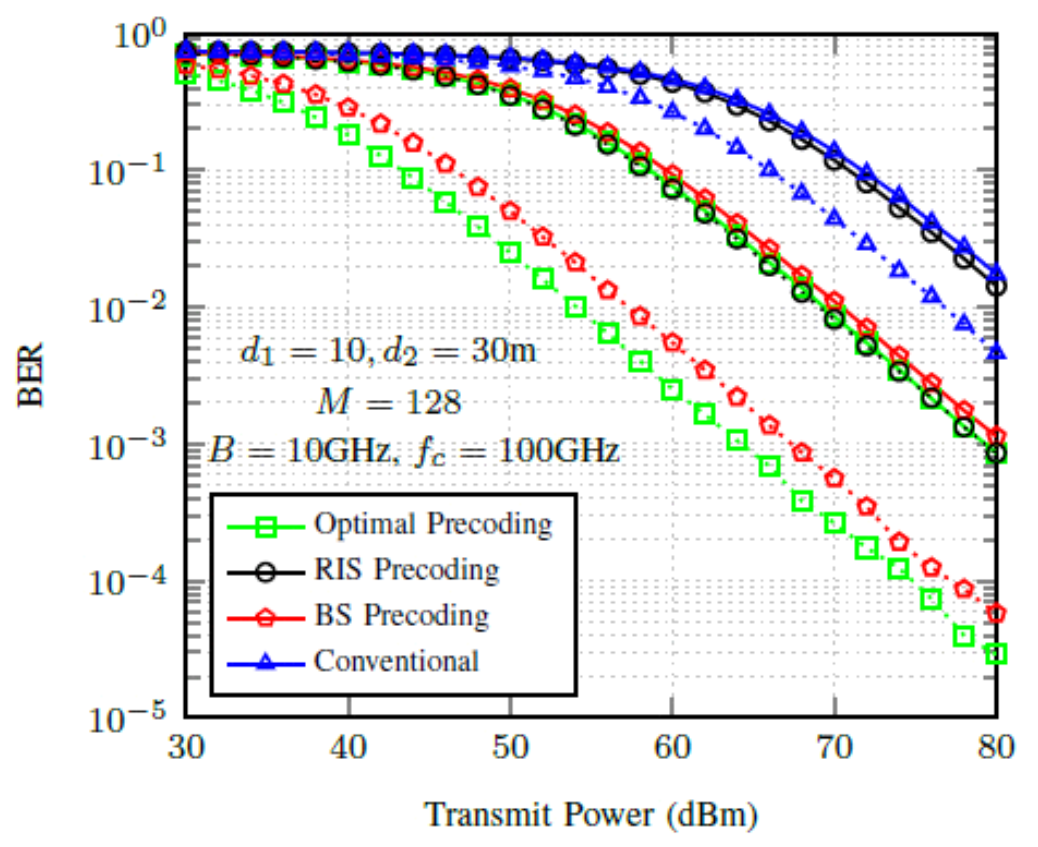

5.1 IQ Mismatch

In THz communications, the RF front-end is partic- ularly vulnerable to IQ mismatch effects due to the extreme sensitivity of components operating at such high frequencies. IQ mismatch occurs when there is an imbalance between the inphase (I) and quadrature (Q) components, leading to signal distortions that de- grade overall system performance. This imbalance, of- ten caused by gain differences, phase errors, or non-idealities in mixers and amplifiers, results in un- wanted interference between I and Q channels. Thus, at higher carrier frequencies, the IQ mismatch sig- nificantly degrades the performance of IMT systems ^[15]. The IQ mismatch transmitted signal is expressed as

where [TeX:] $$\begin{equation} x_m^{\star} \end{equation}$$is the complex conjugate. IQ imbalance coefficients are such that [TeX:] $$\begin{equation} \alpha_1+\alpha_2^*=1 \end{equation}$$, and are given as

where g_t φ_t and are the transmitter gain and the phase mismatch, respectively. The impact of IQ mismatch at the Tx on BER performance is analysed in Fig. 6. The BER performance deteriorates as the IQ mis- match increases, ranging from 1 dB to 10 dB, as ob- served in Fig. 6.

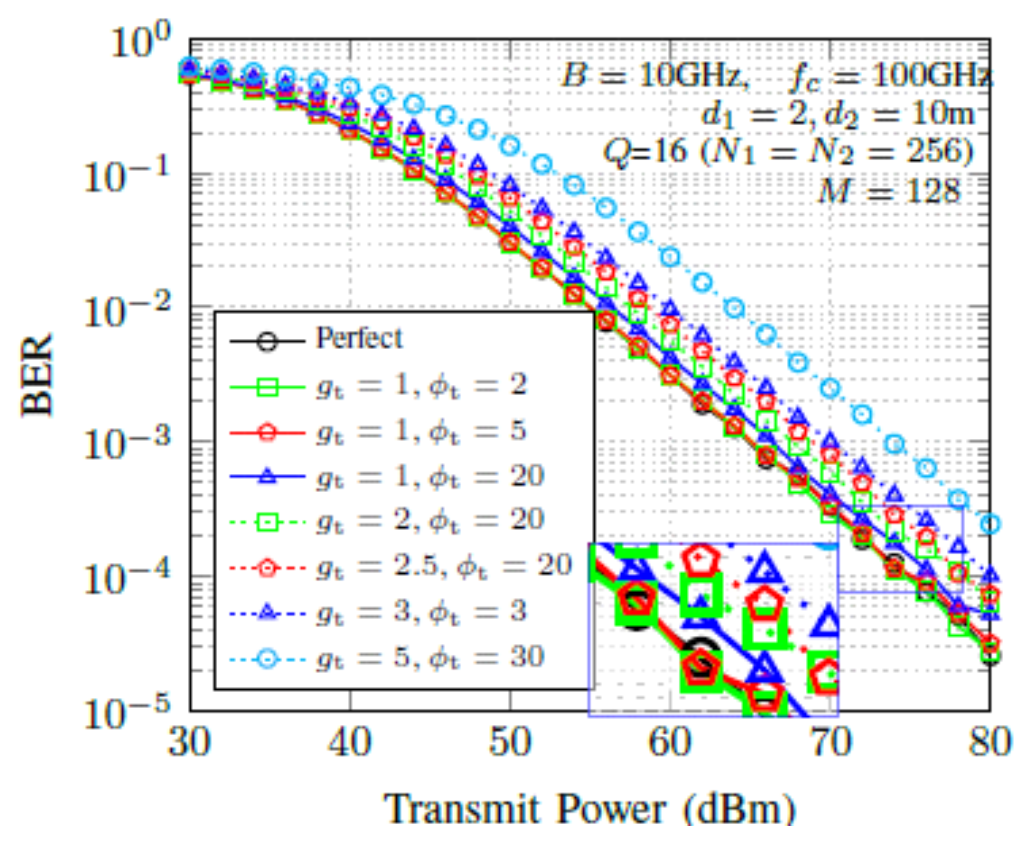IQ mismatch at both Rx and Tx front-end: IQ mismatch at both the Tx and Rx can significantly de- grade the performance of the IMT communication system. At the receiver, IQ mismatch affects the abil- ity to accurately demodulate the signal, as it in- troduces image interference and increases interference level in the desired signal. This leads to a higher BER and reduces signal quality. IQ mismatch at Rx can be modeled as

where [TeX:] $$\begin{equation} \beta_1=0.5\left(1+g_{\mathrm{r}} e^{-j \phi_{\mathrm{r}}}\right), \beta_2=0.5\left(1-g_{\mathrm{r}} e^{j \phi_{\mathrm{r}}}\right) \end{equation}$$ are the same parameters as Tx IQ mismatch. The aver- age BER performance by considering IQ mismatch at both Tx and Rx is shown in Fig. 7. BER perform- ance degrades significantly as compared to IQ mis- match as observed in Fig. 7. Thus, it is crucial to implement compensation techniques to mitigate these impairments, especially in high-frequency applica- tions like 6G networks.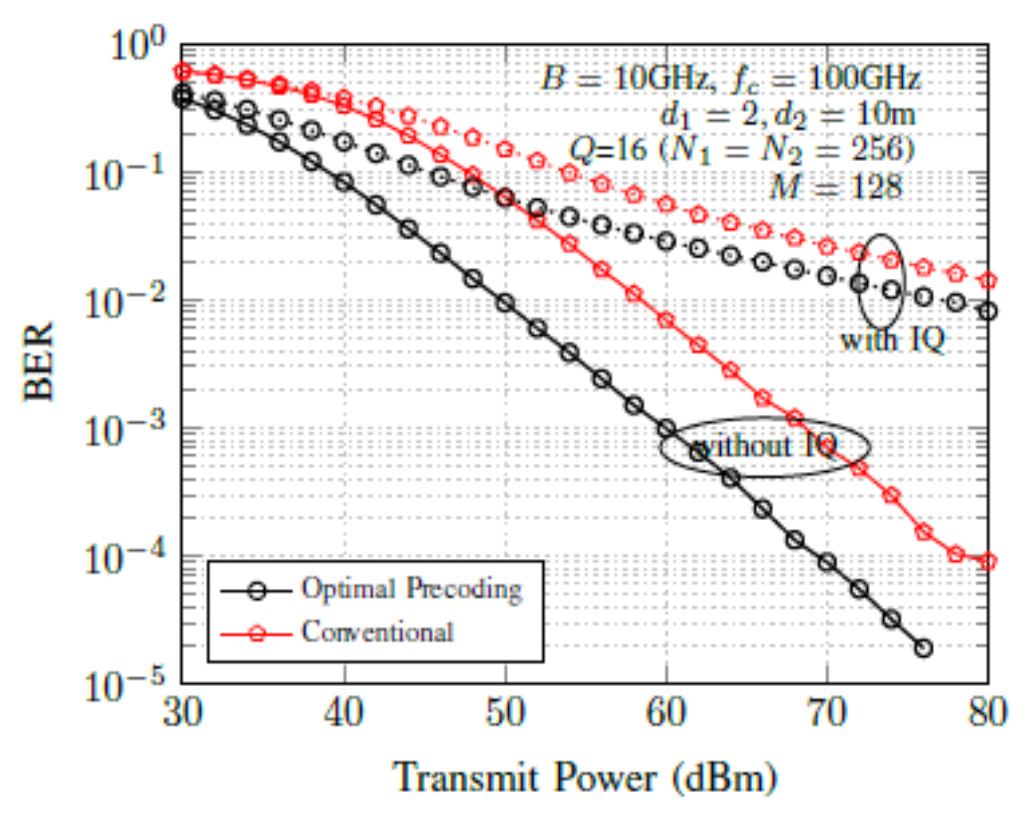

Imper fect CSI: In massive and high-frequency MIMO systems, obtaining perfect channel state in- formation (CSI) is challenging due to several factors. First, the large number of antennas in massive MIMO systems increases the complexity of channel estima- tion, requiring extensive training and feedback overhead. In high-frequency bands, such as terahertz frequencies, the channel experiences rapid fluctuations and high path loss, making real-time and accurate channel estimation difficult. Additionally, hardware impairments and signal propagation issues, like beam squint and severe attenuation, further complicate the acquisition of precise CSI. This makes achieving the perfect CSI impractical in such environments. The im- perfect CSI is expressed as

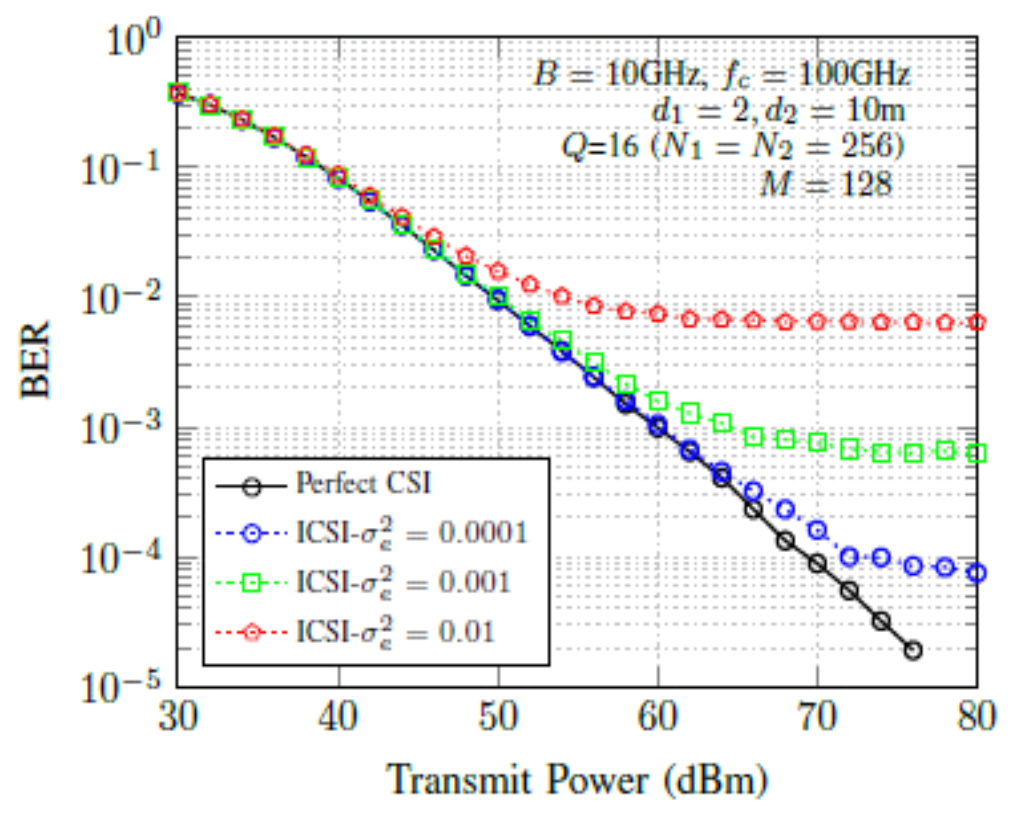
where [TeX:] $$\begin{equation} \widehat{h} \end{equation}$$ is the estimated channel. e denotes the esti- mation error and zero mean Gaussian distributed as [TeX:] $$\begin{equation} \mathbf{e} \sim N\left(0, \sigma_{\mathrm{e}}^2\right) \end{equation}$$. The error plot for different variance [TeX:] $$\begin{equation} \sigma_e^2 \end{equation}$$ is shown in Fig. 8.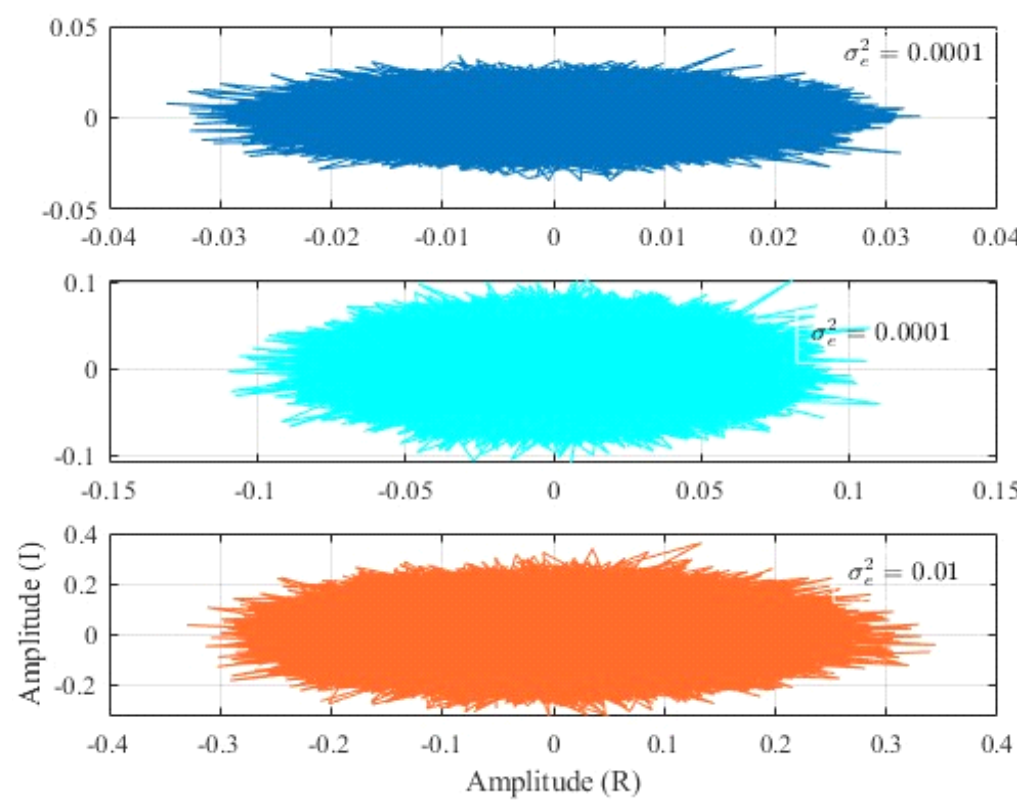

Average BER performance of the IMT system for imperfect CSI scenarios is shown in Fig. 9. It is ob- served that as error variance increases, the BER per- formance degrades significantly as compared to the perfect CSI scenario.

Imperfect CSI plus IQ mismatch: In an IMT sys- tem, achieving perfect CSI and mitigating IQ mis- match is particularly challenging. These factors com- bined make it difficult to obtain accurate CSI and cor- rect IQ mismatches in the IMT system. The average BER performance in the presence of both imperfect CSI and IQ mismatch is shown in Fig. 10. It is ob- served that the BER remains very high and does not reduce as SNR increases when both the transmitter and receiver are affected by IQ mismatch with im- perfect CSI. Furthermore, the imperfect CSI and IQ mismatch cause the BER to saturate, resulting in an error floor in the high SNR region, as observed in Fig. 10.

Ⅵ. Conclusions

We have examined the BER performance within the IMT communication by considering the im- plications of beam splitting in the THz communica- tion, and compared various TD precoding methods in the IMT communication. We have analyzed the ef- fects of factors, such as the number of IRS elements, Tx antennas, and IQ mismatch, on BER. Our analysis highlights that the wide bandwidth of THz exacerbates the beam splitting effect, leading to degradation in BER performance. It is also demonstrated that the ap- plication of the DP precoding can effectively mitigate the beam splitting challenge within the IMT communication. Furthermore, the effect of imperfect CSI and IQ mismatch is highlighted on the BER per- formance in the IMT system.