Low-Complexity Transmit Power Design for Prioritized Wireless Mutual Broadcast

Ⅰ. Introduction

As 6G and AI advance, proximity-aware services en- able localized tasks like neighbor discovery and safety messaging in IoT and vehicle networks^[1]. Wireless mutual broadcast (WMB)^[2-4] supports these services by broadcasting presence and data to nearby nodes. WMB for devices with heterogeneous attrib- utes^[5-7] is crucial for diverse service needs. Some node groups, like safety-critical systems, require higher broadcast message (BM) success rates, but prioritizing them may degrade others’ performance^[7]. This study proposes a low-complexity transmit (Tx) power con- figuration to improve prioritized group performance while maintaining network efficiency.

Stochastic geometry has been widely applied to an- alyze RA-WMB performance in spatial configurations like HPPP^[2], repulsive^[3], and clustered^[4] node distributions. However, these studies did not address heterogeneous nodes. Heterogeneous RA-WMB net- works have been explored for diverse node characteristics. [5] analyzed local broadcasting with varying Tx power levels but lacked joint Tx power optimization. [6] studied networks with half-and full-duplex nodes, offering spatial insights but without Tx power control or prioritization. [7] jointly opti- mized Tx power for-two node groups, balancing one group’ s performance with system-wide degradation but at high computational complexity.

This paper proposes: (i) A joint Tx power op- tim- ization method to prioritize performances across node groups with much lower complexity than [7]; (ii) Closed-form optimal Tx powers for a path loss ex- ponent (PLE) of four.

Notations : [TeX:] $$\begin{equation} \mathbb{E}[f(X)] \end{equation}$$, [TeX:] $$\begin{equation} \mathbb{P}[E] \end{equation}$$, and x^* are the expected value of f(x) with respect to X, the probability of event E, and the optimal value of x. [TeX:] $$\begin{equation} \mathbb{1}[Y=y] \end{equation}$$ is the indicator function, equal to 1 if Y = y and 0 otherwise.

Ⅱ. Performance Models for RA-WMB Using Heterogeneous Transmit Power

This paper investigates heterogeneous RA-WMB networks with nodes using different Tx powers. HPPP simplifies analysis for slotted Aloha, while advanced access schemes and clustered distributions, exhibiting trends similar to HPPP^[3,4], are left for future work. In this HPPP, node i and its location are denoted by X_i, with a Tx power value of [TeX:] $$\begin{equation} m_i \in\left\{p_1, \ldots, p_G\right\} \end{equation}$$ de- termined by priority or service requirements. Priority-based Tx power can be managed via Tx pow- er control protocols, e.g., periodic broadcasts of Tx power policies by header nodes, including the Tx power derived in this study. The nodes and their Tx power values are collectively modeled as the marked HPPP [TeX:] $$\begin{equation} \hat{\Phi} \triangleq\left\{\left(X_i, m_i\right)\right\} \end{equation}$$. Each node transmits its BM with TxPr ν, randomly selecting one of K orthogonal resource blocks (RBs), and receives with probability 1 - ν. This study focuses on varying Tx power levels with a common TxPr ν, leaving TxPr variation for future work. Wireless channels assume path loss with PLE α and Rayleigh fading, as Nakagami-mhas mini- mal impact on overall trends^[2]. Node i’ s transceiving status T_i is 1 for transmission and 0 for reception. Interference status U_i,j is 1 if node j transmits on the same RB as node i, and 0 otherwise. For the typical node X₀ at the origin decoding a BM from X_i with Tx power m_i, the SINR is [TeX:] $$\begin{equation} \Xi_i=\frac{m_i h_i\left|X_i\right|^{-\alpha}}{I\left(X_i\right)+\sigma^2} \end{equation}$$ where [TeX:] $$\begin{equation} I\left(X_i\right)=\sum_{j:\left(X_j, m_j\right) \in \Phi \backslash\left\{\left(X_i, m_i\right)\right\}} \mathbb{1}\left[U_{i, j}=1\right] m_j h_j\left|X_j\right|^{-\alpha} \end{equation}$$, and [TeX:] $$\begin{equation} \sigma^2=\frac{\tilde{\sigma}^2}{A} \end{equation}$$. [TeX:] $$\begin{equation} \tilde{\sigma}^2 \end{equation}$$ is noise power, Ais path loss gain at unit distance, h_i is the Rayleigh fading gain, and |X_j| is the distance of X_j from X₀. Decoding succeeds if [TeX:] $$\begin{equation} \Xi_i \neq \xi \end{equation}$$.

Nodes with similar attributes are grouped, with each group assigned a Tx power from [TeX:] $$\begin{equation} \left\{p_1, \ldots, p_G\right\} \end{equation}$$, and nodes in a group use the same Tx power.

This Tx power configuration is expressed as [TeX:] $$\begin{equation} \Omega \triangleq \left\{\left(p_1, \rho_1\right), \ldots,\left(p_G, \rho_G\right),\right. \end{equation}$$, where [TeX:] $$\begin{equation} \rho_g \triangleq \mathbb{P}\left[m_i=p_g\right] \end{equation}$$ for [TeX:] $$\begin{equation} \left(X_i, m_i\right) \in \hat{\Phi} \end{equation}$$. Given Ω and ν , the performance of group g, Sg (Ω , ν), is defined as

which means the average number of BMs that the typ- ical node successfully receives from nodes in group g. The overall performance is given by [TeX:] $$\begin{equation} S(\Omega, \nu) \triangleq\sum_{g=1}^G S_g(\Omega, \nu) \end{equation}$$, representing the average number of BMs received from all groups’ nodes. To compare with uniform Tx power, the performance under a com- mon power p is defined as [TeX:] $$\begin{equation} S_o(p, \nu) \triangleq S((p, 1), \nu) \end{equation}$$. [7] concisely expressed S and S_gin terms of S_o, as follows.

Lemma 1 Given Ω and ν, when [TeX:] $$\begin{equation} \Delta(\alpha) \triangleq \frac{\sin (2 \pi / \alpha)}{2 \pi / \alpha} \end{equation}$$,

Further, when [TeX:] $$\begin{equation} \Theta(\Omega) \triangleq \frac{\max _{0<v\lt1} S(\Omega, \nu)}{\max _{0\ltv\lt1} S_o(\bar{p}, \nu)}, \quad \Theta(\Omega)\lt1, \end{equation}$$

[TeX:] $$\begin{equation} \lim _{K \rightarrow \infty} \Theta(\Omega)=\frac{\mathbb{E}\left[P^{2 / \alpha}\right]}{\mathbb{E}[P]^{2 / \alpha}}\lt1, \text { and } \lim _{\sigma^2 \rightarrow 0} \Theta(\Omega)=1 \end{equation}$$

Proof In [7], see Theorem 1 for S , Corollary 2 for S_g, and Corollary 3 for Θ.

Ⅲ. Transmit Power Design for Performance Prioritization

This section jointly optimizes Tx power for node groups to enhance the performance of a prioritized group (i.e., group 1) while maintaining overall per- formance above a certain level. Performance prioriti- zation reduces overall performance S because Θ(Ω) <1 from Lemma 1. For meaningful prioritization, [TeX:] $$\begin{equation} p_1>\bar{p} \end{equation}$$ is assumed, where [TeX:] $$\begin{equation} \bar{p}=\mathbb{E}[P]=\sum_{i=1}^G \rho_i p_i \end{equation}$$, with P as the random variable representing node group Tx powers.

[7] focused on two node groups and formulated the problem with the overall performance loss require- ment Θ(Ω)≥η for 0<η<1, defined in Lemma 1, like

In this problem, the computation of Θ(Ω) requires complex cascaded iterations evaluating the numerical integrals in S and So, finding their maximum TxPr values using the golden section algorithm, and apply- ing the bisection method to the overall process for the final solution. This Θ reaches its minimum in the coverage-limited scenario and gradually increases with interference, converging to one in an interfer- ence-limited environment^[7]. To reduce the complex- ity, this paper replaces Θ(Ω) with its lower bound or worst-case value, [TeX:] $$\begin{equation} \lim _{K \rightarrow \infty} \Theta(\Omega)=\frac{\mathbb{E}\left[P^{2 / \alpha}\right]}{\mathbb{E}[P]^{2 / \alpha}} \end{equation}$$, like

Unlike Problem (5) considering only two groups, the proposed Problem (6) generalizes to any number of groups. And, it replaces complex max_0<ν<1 S(Ω, ν) and max_0<ν<1 [TeX:] $$\begin{equation} S_o(\bar{p}, v) \end{equation}$$ with simpler [TeX:] $$\begin{equation} \mathbb{E}\left[P^{2 / \alpha}\right] \end{equation}$$ and [TeX:] $$\begin{equation} \mathbb{E}\left[P\right]^{2 / \alpha} \end{equation}$$, significantly reducing complexity.

Theorem 1 Problem(6) isequivalenttothefollowing problem with [TeX:] $$\begin{equation} p_2, \ldots, p_G \end{equation}$$ assigned equally to p_o:

where [TeX:] $$\begin{equation} \rho_o \triangleq 1-\rho_1 \end{equation}$$. Then, for Problem (7), if [TeX:] $$\begin{equation} \eta > \rho_1^{1-2 / \alpha} p_1^* \end{equation}$$ is the unique solution of f (x) = 0 and [TeX:] $$\begin{equation} p_2^*=\cdots=p_G^*=\frac{\bar{p}-\rho_1 p_1^*}{\rho_o} \end{equation}$$. Here, [TeX:] $$\begin{equation} f_p(x) \triangleq \rho_o^{1-\alpha / 2}\left(\bar{p}-\rho_1 x\right)^{2 / \alpha}+\rho_1 x^{2 / \alpha}-\eta \bar{p}^{2 / \alpha} \end{equation}$$ and f_p(x) decreases monot - onically in x.

Otherwise, [TeX:] $$\begin{equation} p_1^*=\bar{p} / \rho_1 \end{equation}$$ and [TeX:] $$\begin{equation} p_2^*=\cdots=p_G^*=0 \end{equation}$$.

Proof Assume p₁ is fixed. Then, maximizing (6a) re- duces to minimizing [TeX:] $$\begin{equation} \sum_{i=2}^G \rho_i p_i^{2 / \alpha} \end{equation}$$. By the arith- metic-geometric mean inequality, [TeX:] $$\begin{equation} \sum_{i=2}^G \rho_i p_i^{2 / \alpha} \ge \left(\sum_{i=2}^G \rho_i\right) \prod_{i=2}^G\left(p_i^{2 / \alpha}\right)^{\rho_i / \sum_{i=2}^G \rho_i} \end{equation}$$, with equality when [TeX:] $$\begin{equation} p_2=\ldots=p_G \end{equation}$$. Thus, minimizing [TeX:] $$\begin{equation} \sum_{i=2}^G \rho_i p_i^{2 / \alpha} \end{equation}$$ ensures that [TeX:] $$\begin{equation} p_2=\ldots=p_G \end{equation}$$ are set to the same value, p_o. As a result, maximizing (6a) for all [TeX:] $$\begin{equation} p_1, \ldots, p_G \end{equation}$$ becomes equivalent to minimizing [TeX:] $$\begin{equation} \frac{\rho_o p_o^{2 / \alpha}}{\rho_1 p_1^{2 / \alpha}} \end{equation}$$, or equivalently, maximizing [TeX:] $$\begin{equation} \frac{p_1}{p_o} \end{equation}$$. Hence, Problems (6) and (7) are equivalent.

From [7, Lemma 1], [TeX:] $$\begin{equation} \rho_1 p_1^{2 / \alpha}+\rho_o p_o^{2 / \alpha} \end{equation}$$ decreases as p₁ increases. (7a) increases with p₁. Thus, p₁ can grow until the equality in (7b) is met. Because [TeX:] $$\begin{equation} p_1 \leq \bar{p} / \rho_1 \end{equation}$$ from [TeX:] $$\begin{equation} \mathbb{E}[P]=\bar{p} \end{equation}$$, if (7b) holds at [TeX:] $$\begin{equation} p_1=\bar{p} / \rho_1 \end{equation}$$, then [TeX:] $$\begin{equation} p_1^*=\bar{p} / \rho 1 \end{equation}$$. Otherwise, i.e., if [TeX:] $$\begin{equation} \rho_1\left(\bar{p} / \rho_1\right)^{2 / a}\lt\eta \bar{p}^{2 / a}\left(\text { or } \eta>\rho_1^{1-2 / \alpha}\right) \end{equation}$$, p₁ must satisfy the equality in (7b). Combining this with [TeX:] $$\begin{equation} \mathbb{E}[P]=\bar{p} \end{equation}$$ leads to [TeX:] $$\begin{equation} f_p\left(p_1^*\right)=0 \end{equation}$$, where f_p(x) monotonically decreases. Thus, f_p(x) = 0 has a unique solution, which is [TeX:] $$\begin{equation} p_1^* \end{equation}$$. The corresponding [TeX:] $$\begin{equation} p_o^* \end{equation}$$ can be derived from [TeX:] $$\begin{equation} \rho_1 p_1+\rho_o p_o=\bar{p} \end{equation}$$.

Theorem 1 demonstrates that optimizing two node groups is equivalent to considering any number of groups, with the optimal Tx power easily found using the bisection method on the simple f_p(x) = 0.

Corollary 1 When α = 4 and [TeX:] $$\begin{equation} p_1>\bar{p} \end{equation}$$, if [TeX:] $$\begin{equation} \eta>\sqrt{\rho_1} \end{equation}$$,

If [TeX:] $$\begin{equation} \eta \leq \sqrt{\rho_1}, p_1^*=\bar{p} / \rho_1 . p_2^*=\ldots=p_G^*=\frac{\bar{p}-\rho_1 p_1^*}{\rho_o} \end{equation}$$

Proof Applying the results of Theorem 1 for α = 4 and considering [TeX:] $$\begin{equation} p_1>\bar{p} \end{equation}$$, the results are derived.

Ⅳ. Numerical Results and Discussions

This section evaluates the Tx power design from Section III using the model in Section II and parame- ters in Table 1, with [TeX:] $$\begin{equation} \mathbb{E}[P] \end{equation}$$ fixed at [TeX:] $$\begin{equation} \bar{p} \end{equation}$$. From Theorem 1, the Tx power design of (6) for any number of node groups is equivalent to (7) with G=2; thus, the per- formance is evaluated with G=2.

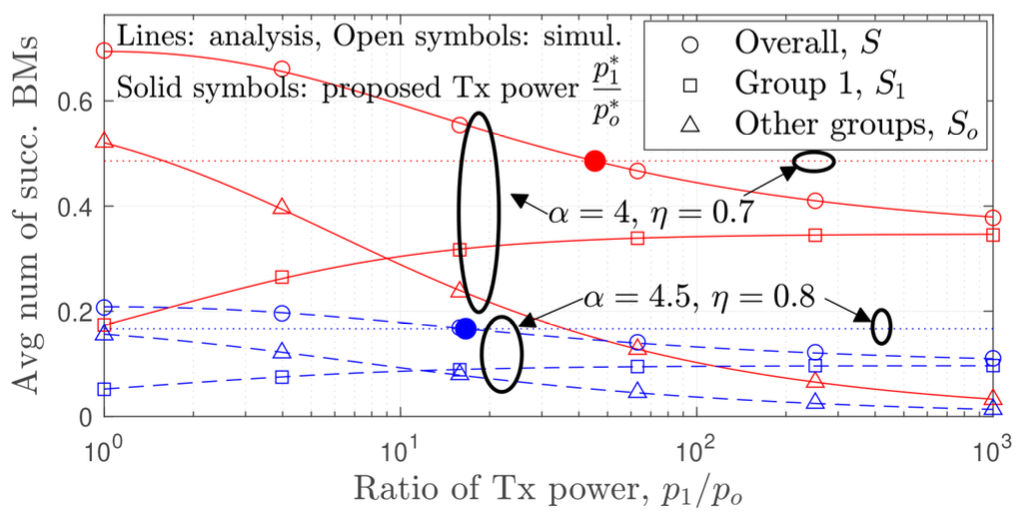
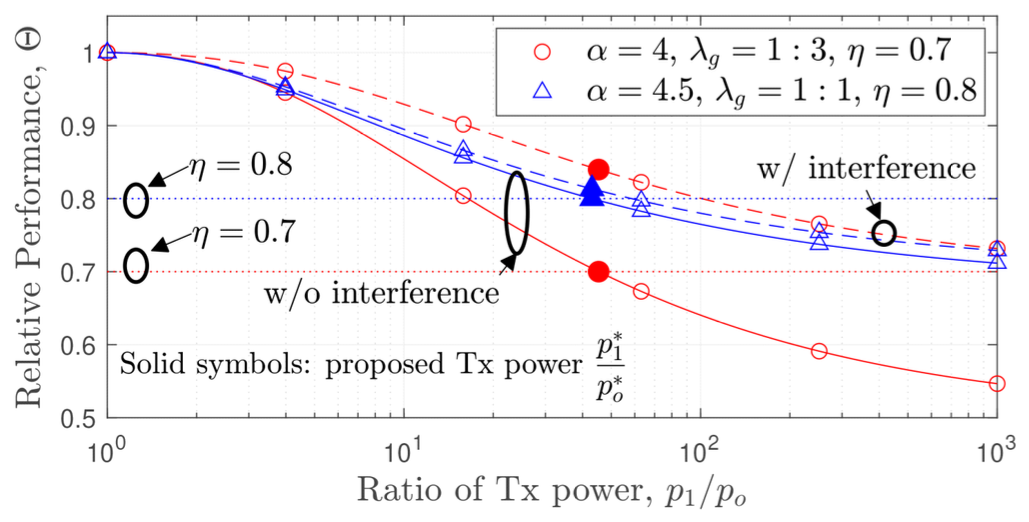
Fig. 1 presents the overall and group-specific per- formance as a function of p₁ / p_o, with [TeX:] $$\begin{equation} \mathbb{E}[P]=\bar{p} \end{equation}$$ held constant while varying p₁ and p_o. A coverage-limited environment without interference is applied to validate the basic properties of prioritized WMB and the accu- racy of the proposed method. The values of S and S_g, determined by Lemma 1, align perfectly with the simulation results. As p₁ increases, S decreases. The optimal values [TeX:] $$\begin{equation} p_1^* \end{equation}$$ and [TeX:] $$\begin{equation} p_2^* \end{equation}$$, easily obtained from the solution of simple f_p(x) = 0 in Theorem 1 or the closed form in Corollary 1, are marked with solid symbols on the graph and meet the minimum requirement ηS

Fig. 1.

Tx power design for prioritization in interference- free scenarios. [λ _g = 1 : 3]

Fig. 2.

Impact of interference on design performance.

Fig. 2 examines the performance deviation of the proposed method, which applies the worst-case per- formance loss requirement from an interference-free case, compared to actual interference scenarios. As ex- pected, the method sets the performance loss require- ment conservatively under interference, ensuring ro- bustness for dynamic environments. In scenarios with reduced interference impact (e.g., α = 4.5) and more uniform node distributions (e.g., λ_g = 1:1), where [TeX:] $$\begin{equation} \mathbb{E}\left[P^{2 / \alpha}\right] \end{equation}$$ and [TeX:] $$\begin{equation} \mathbb{E}[P]^{2 / \alpha} \end{equation}$$ differ less, the method demonstrates both robustness and high accuracy. Thus, the proposed approach is highly effective in scenarios requiring ro- bust performance loss guarantees and low complexity.

Ⅴ. Conclusions

This paper proposed a method to jointly optimize node group transmit power, using a bisection search on a simple function for general path loss exponents (PLEs) and a closed-form expression for a PLE of four, with the aim of enhancing a specific group’s performance while limiting overall loss. The method imposed stricter conditions under interference but de- livered robust performance across diverse scenarios, making it suitable for applications requiring robust- ness and low complexity. Future study will explore the impacts of more practical channel and node dis- tribution models.