IndexFiguresTables |
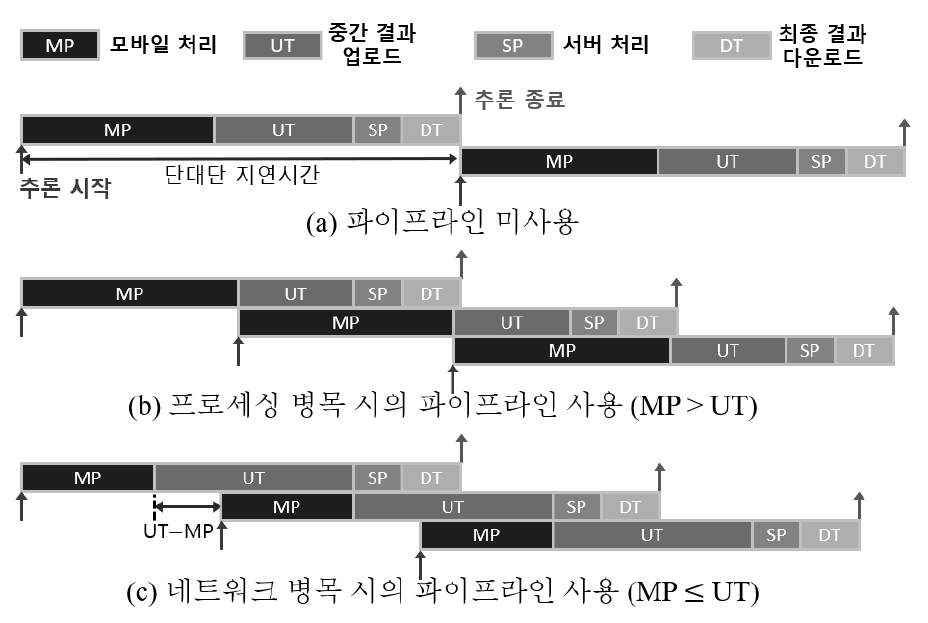
Junsoo Park♦ and Yeongjin Kim°DNN Model Partition and Resolution Control for Edge-Assisted Mobile Vision AIAbstract: With the advancement of mobile device and network performance, the industry for mobile vision applications, such as image classification and object detection, is rapidly growing. When designing mobile vision applications, employing mobile edge computing (MEC) based on deep learning model partitioning can significantly improve the quality of user experience (QoE). Research on deep learning model partitioning has advanced in various directions over time, but until now, there has been no study that simultaneously partitionizes deep learning models by layers and adjusts the input frame size. Our proposed algorithm, Parecon, is based on Lyapunov optimization and dynamically adjusts 1) the number of frames to be processed, 2) model partition points, and 3) input frame size at each time slot. The proposed algorithm simultaneously optimizes processed fps, E2E latency, and top-1 accuracy. Through simulations, we confirmed that Parecon achieves a significant improvement in fps compared to existing algorithms while maintaining simular E2E latency and top-1 accuracy. Keywords: Deep learning , DNN model partitioning , resolution control , mobile vision application , quality of experience , mobile edge computing 박준수♦, 김영진°엣지 컴퓨팅 기반 모바일 비전 AI를 위한 DNN 모델 분할 및 해상도 최적화요 약: 모바일 기기 및 네트워크 성능의 향상과 함께 이미지 분류, 물체 인식과 같은 모바일 비전 애플리케이션 산업은 빠르게 성장하고 있다. 모바일 비전 애플리케이션을 설계할 때, 딥러닝 모델 파티셔닝에 기반한 모바일 엣지컴퓨팅(MEC)을 바탕으로 한다면 사용자 경험 품질(QoE)을 향상하는 데 큰 도움이 된다. 딥러닝 모델 파티셔닝에대한 연구는 그동안 여러 방향에 걸쳐 발전해 왔으나, 이전까지는 딥러닝 모델을 레이어 단위로 나눔과 동시에 입력 프레임의 크기를 조절하는 연구는 없었다. 본 연구는 Lyapunov 최적화에 기반하여 타임슬롯마다 1) 처리할 프레임의 수, 2) 모델 파티션 포인트, 3) 입력 프레임의 사이즈를 동시에 조절하는 알고리즘 Parecon을 제안한다. 제안된 알고리즘은 처리 fps, 단대단 지연 시간, top-1 정확도를 동시에 최적화하며, 시뮬레이션을 통해 Parecon이기존의 알고리즘에 비해 단대단 지연 시간, top-1 정확도를 유지하면서도 fps를 크게 향상시키는 것을 확인한다. 키워드: 딥러닝, DNN 모델 파티셔닝, 해상도 조절, 모바일 비전 애플리케이션, 사용자 경험 품질, 모바일엣지 컴퓨팅 Ⅰ. 서 론최근 모바일 기기 및 네트워크의 성능, 딥러닝 기술의 발달과 함께 자율주행 자동차, 스마트폰, 드론과 같은 모바일 기기에서 딥러닝 모델에 기반한 모바일 비전 애플리케이션을 사용하는 경우가 늘어나고 있다. 딥러닝 모델을 처리하는 위치에 따라, 처리 방식을 모바일 컴퓨팅과 엣지 컴퓨팅으로 분류할 수있다. 모바일 컴퓨팅에서는 모든 딥러닝 모델의 처리를 모바일 기기가 맡으며, 이 경우 지속적인 모바일 하드웨어의 발전에도 불구하고 성능의 제한이 존재한다. 엣지 컴퓨팅에서는 모바일 기기는 단지 입출력 기기의 역할 만을 수행하며, 엣지 서버에서 딥러닝 연산이 이루어진다. 일반적으로 엣지 서버의 성능은 모바일 기기보다 훨씬 높으므로 이 경우에는 성능 문제가 발생하지는 않으나, 네트워크 상태가 좋지 않은 상황에서 제대로 서버를 사용하기 어렵다는 한계가 있다. 모바일 엣지 컴퓨팅(MEC)은 두 처리 방식의 장점만을 결합했다. MEC는 이진 결정 MEC와 딥러닝 모델 파티셔닝에 기반한 MEC로 나눌 수 있는데, 이진 결정 MEC에서는 모바일 컴퓨팅과 엣지 컴퓨팅 중 하나만을 선택할 수 있으며, 실시간으로 변화하는 네트워크의 상태나 모바일 기기가 사용 가능한 에너지 등을 고려하여 QoE를 높일 수 있는 방향으로 모바일 컴퓨팅과 엣지 컴퓨팅 중 하나를 결정하는 연구가 진행되어왔다[1-8]. 한편 딥러닝 모델 파티셔닝에 기반한 MEC에서는 딥러닝 모델을 여러 개의 레이어 그룹으로 분리한다. 이 경우 딥러닝 모델의 처리 방식을 결정하는 시스템은 모바일 컴퓨팅이나엣지 컴퓨팅을 선택할수도 있지만, 상황에 따라 레이어 그룹 일부는 모바일에서 처리한 뒤, 중간 결과를 엣지 서버로 전송하여 나머지 레이어 그룹을 처리하는 것이 가능하다. 딥러닝 모델 파티셔닝을 사용할 경우 시스템은 더 많은 선택지가 생겨나며, 따라서 딥러닝 모델 파티셔닝에 기반한 MEC는 이진 결정 MEC보다 변화하는 환경에 더 유연하게 대응할 수 있다[9-13]. 그러나 이제까지 딥러닝 모델 파티셔닝과 입력 프레임의 크기 조절을 동시에 수행하는 연구는 존재하지 않았다. 입력 프레임의 크기를 원본 대비 줄일 경우, 자연스럽게 모바일 기기가 처리해야 하는 데이터의 양과 중간 결과 크기가 감소하며, 이에 따라 처리 속도가 증가할 것이라고 기대할 수 있다. 하지만 동시에 입력 프레임 크기의 감소는 추론 정확도의 손실을 야기하며[14], 지나치게 입력 프레임 크기를 크게 줄일 경우 딥러닝 모델의 본래 성능을 제대로 발휘할 수 없다. 본 연구는 처리 fps와 정확도 사이에서 균형을 찾고자 한다. 여기에 더해, 본 연구는 처리 fps를 높이기 위해 기존의 딥러닝 모델 파티셔닝 관련 연구에서 사용되었던[15] 파이프라인 개념을 도입했다. 그림 1(b)는 모바일 처리 시간이 업로드 시간보다 긴 경우에 파이프라인이 작동하는 방식을 보여준다. 파이프라인을 사용하면 n번째 프레임의 중간 결과가 네트워크를 통해 엣지 서버로 전송되는 순간, n+1번째 프레임의 모바일 처리가 시작됨으로써 동시에 여러 프레임을 처리하는 것이 가능하다. 그림 1(c)는 업로드 시간이 모바일 처리 시간보다 긴 경우에 파이프라인이 작동하는 방식을 보여준다. 중간 결과가 연속으로 전송될 수 있도록 n번째 프레임의 중간 결과가 전송되는 와중에 n+1번째 프레임의 모바일 처리가 시작된다. 파이프라인 구조를 구현하기 위해서는 프로그램에서 모바일 처리 프로세스, 업로드 프로세스, 다운로드 프로세스가 독립적으로 작동해야 한다. 일반적으로 처리 fps가 증가하면 자연스럽게 한 프레임당 소요되는 단대단 지연 시간은 감소하지만, 파이프라인을 사용할 경우 프로세스 간에 데이터를 주고받는 과정에서 추가지연이 발생하기 때문에 처리 속도와 단대단 지연 시간 사이에서도 균형을 찾아야 한다. 종합하자면, 본 연구는 처리 fps, 단대단 지연 시간, 정확도를 동시에 최적화하는 알고리즘을 설계하는 것을 목표로 한다. 만약 3개의 요소 사이에서 적절한 균형점을 찾을 수 있다면, 정확도 및 지연 시간의 손실을 최소화하면서 처리 fps를 극대화할 수 있을 것이다. 이를 위해 본 연구에서는 가상 큐 기반 Lyapunov 최적화를 활용하여 1) 파티션 포인트, 2) 처리 fps, 3) 입력 프레임 크기를 동적으로 제어하는 Parecon 알고리즘을 제안한다. 제안한 Parecon 알고리즘은 단대단 지연 시간 및 정확도와 관련된 제약 조건을 지키면서 처리 fps를 최대화한다. 또한, 시뮬레이션을 통해 Parecon 알고리즘의 성능을 측정하고, 기존에 제안된 알고리즘과 비교해 어느 정도의 성능 향상을 보이는지 확인한다. Ⅱ. 시스템 모델2.1 서비스 모델그림 2는 본 연구의 시스템 모델 구조이며, 모바일 단말이 비전 애플리케이션을 사용하고, 모바일 기기와 MEC 서버 모두 사전 학습된 딥러닝 모델 m을 메모리에 올려두고 있다. 예를 들어, 모바일 단말에서 물체 인식을 위하여 모바일 단말과 MEC 서버 모두 동일한 EfficientNetV2-S 모델을 메모리에 올려둔다. 본 연구의 타임슬롯은 [TeX:] $$t \in T=\{0,1, \cdots, T-1\}$$로 구성되어 있으며, 단위 시간 간격은 [TeX:] $$\Delta t$$(second)로 둔 시간에 따라 동작하는 시스템을 고려한다. 모바일 비전 애플리케이션은 타임슬롯마다 시작 추론을 위하여 w(bits) 크기의 a(t)(frames) 개를 생성하고, 이는 모바일 단말의 추론을 위한 입력 데이터로 사용한다. 모바일 단말은 입력되는 데이터에 대해서 처리하고자 하는 데이터의 수 [TeX:] $$b(t) \in \{0, \cdots, a(t)\}$$를 결정한다. 또한, 모바일 비전 애플리케이션에 입력된 프레임은 크기 조정 팩터 [TeX:] $$S \in\left\{s_1, s_2, \cdots, 1\right\}$$에 의해 재조정되며, 최종적으로 딥러닝 모델이 타임슬롯 t마다 입력받는 이미지의 크기는 ws(t)가 된다. s(t)=1일 경우 원본 크기가 그대로 유지되며, 1 이하로 줄어드는 경우 그만큼 프레임의 크기가 감소한다. 그림(Fig.) 2. 입력 프레임의 크기 조정과 딥러닝 모델 파티셔닝을 함께 수행하는 MEC 시스템 구조. (MEC system architecture that performs input frame resizing and deep learning model partitioning simultaneously.) 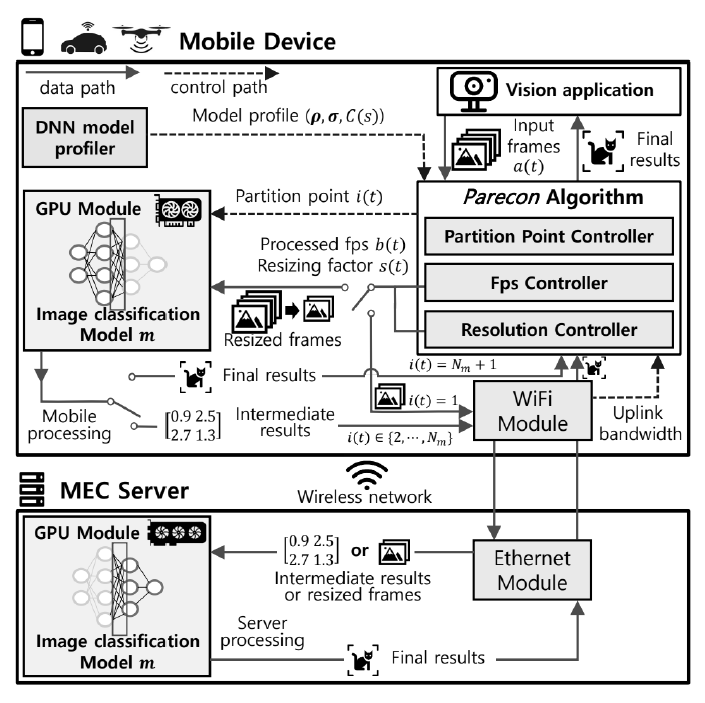 사전 학습된 딥러닝 모델 m은 convolution, maxpool과 같이 특정 작업을 수행하는 여러 레이어로 구성된다. 본 연구에서 사용한 모델은 22.1M 개의 파라미터를 갖는 EffcientNetV2-S이며 ImageNet-1k 데이터 세트에 기반하여 사전 훈련되어있다. 이러한 레이어의 출력 결과는 연속된 다음 레이어의 입력이 된다. 본 연구에서는 모델 m을 [TeX:] $$N_m$$개의 레이어 그룹으로 나누어, [TeX:] $$\mathrm{LG}_m=\left\{l_m^1, l_m^2, \cdots l_m^{N_m}\right\}$$로 표현한다. 레이어 그룹 [TeX:] $$l \in \mathrm{LG}_{\mathrm{m}}$$은 추론 연산을 분할 하기 위한 가장 작은 단위이다. 이때, 레이어 그룹 l은 residual block, parallel 레이어, route 레이어 등을 포함한 하나 이상의 레이어들로 이루어져 있다. 단일 프레임의 추론을 완료하려면 프레임이 모든 [TeX:] $$\mathrm{LG}_{\mathrm{m}}$$의 레이어 그룹에서 순차적으로 처리되어야 한다. 상황에 따라 일부 상위 레이어 그룹은 모바일 단 말에서 프로세싱된 후, 그에 따른 결과를 MEC 서버로 전송한 후, 남아있는 나머지 레이어 그룹은 MEC 서버에서 프로세싱하여 추론을 진행할 수 있다. 즉, 딥러닝 모델 파티셔닝을 통하여 모바일 단말과 MEC 서버가 추론 연산을 분담하는 것이 가능하다. 이에 따라 모바일 단말은 모바일 단말과 MEC 서버 간 프로세싱 연산을 나누기 위하여 매 타임슬롯 t마다 파티션 포인트 [TeX:] $$i(t) \in\left\{1,2, \cdots, N_m+1\right\}$$를 결정한다. 결정된 파티션 포인트 i(t)에 따른 동작은 다음과 같다.
[TeX:] $$\left\{\begin{array}{l} i(t)=1: \mathrm{MEC} \text { 서버가 } \mathrm{LG}_m \text { 를 처리, } \\ i(t)=N_m+1: \text { 모바일 단말이 } \mathrm{LG}_{\mathrm{m}} \text { 를 처리, } \\ \text { otherwise: 모바일 단말이 }\left\{l_m^1, \cdots, l_m^{i(t)-1}\right\} \text { 를 처리 후, } \\ \text { MEC 서버가 }\left\{l_m^{i(t)}, \cdots, l_m^{N_m}\right\} \text { 를 처리 } \end{array}\right.$$ 각 레이어 그룹의 특성을 반영하기 위해 단일 비트를 처리하는 데 필요한 GPU 사이클 수를 나타내는 processing density [TeX:] $$\rho_m^{l, s}(\text { cycles } / \text { bit })$$를 정의한다. 만약 레이어 그룹 l이 필터의 크기가 주어진 합성곱 계층을 포함하고 있을 경우, [TeX:] $$\rho_m^{l, s}$$는 s에 따라 달라질 수 있다. 반면 레이어 그룹 l이 동일한 크기의 입력만 허용하는 dense 레이어로만 이루어졌을 경우 [TeX:] $$\rho_m^{l, s}$$는 s에 대해 동일하다. 또한, 각 레이어 그룹별로 입력 데이터 대비 출력 데이터 크기가 다르다. 이러한 비율을 bit conversion ratio [TeX:] $$\sigma_m^{l, s} \text { (bits/bit) }$$로 정의한다. process density와 마찬가지로, [TeX:] $$\sigma_m^{l, s}$$의 값은 s에 따라 달라질 수 있다. 파티션 포인트 i, 크기 조정 팩터 s에 대해, 모바일 기기(md)와 MEC 서버(es)의 processing density와 bit conversion ratio는 다음과 같이 표현된다.
(1)[TeX:] $$\begin{cases}\rho_{m, \mathrm{md}}^{i, s}=\sum_{j=0}^{i-1} \rho_m^{l, s} \prod_{l^{\prime}=0}^{l-1} \sigma_m^{l, s^{\prime}}, & \rho_{m, \mathrm{es}}^{i, s}=\sum_{l=i}^{N_m} \rho_m^{l, s} \prod_{l^{\prime}=0}^{l-1} \sigma_m^{l^{\prime}, s} \\ \sigma_{m, \mathrm{md}}^{i, s}=\prod_{l=0}^{i-1} \sigma_m^{l, s}, & \sigma_{m, \mathrm{es}}^{i, s}=\prod_{l=0}^{N_m} \sigma_m^{l, s}\end{cases}$$여기서 모든 크기 조정 팩터 [TeX:] $$s \in S$$에 대해 [TeX:] $$\rho_m^{0, s}=0$$이고, [TeX:] $$\sigma_m^{0, s}=1$$이다. [TeX:] $$\rho_{m, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}} \text { 및 } \rho_{m, \mathrm{es}}^{\mathrm{i}, \mathrm{~s}}$$는 프레임 크기 ws(t)에 대해 모바일 기기 및 MEC 서버가 경험하는 process density이며, [TeX:] $$\rho_{m, \mathrm{md}}^{1, s}=0, \rho_{m, \mathrm{es}}^{N_{m+1}, s}=0$$이다. 따라서 모바일 기기와 MEC 서버의 작업량은 각각 [TeX:] $$w s(t) \rho_{m, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}} \text { 와 } w s(t) \rho_{m, \mathrm{es}}^{\mathrm{i}, \mathrm{~s}}$$이다. 마찬가지로 [TeX:] $$\sigma_{m, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}} \text { 및 } \sigma_{m, \mathrm{es}}^{\mathrm{i}, \mathrm{~s}}$$는 모바일 기기와 MEC 서버가 경험하는 bit conversion ratio이다. 예외적으로 [TeX:] $$\sigma_{m, \mathrm{md}}^{N_{m+1}, s}=0, \quad \sigma_{m, \mathrm{es}}^{N_{m+1}, s}=0$$이며, 이는 [TeX:] $$i=N_m+1$$일 경우 모바일에서 모든 데이터를 처리하기 때문이다. 결과적으로 업로드에 필요한 중간 결과 크기는 [TeX:] $$w s(t) \sigma_{m, \mathrm{md}}^{i, s}$$이고, 최종 결과 크기는 [TeX:] $$w s(t) \sigma_{m, \mathrm{es}}^{i, s}$$이다. 2.2 정확도 모델s(t)를 줄이면 입력 프레임의 크기가 줄어 추론 속도가 높아지지만, 동시에 추론 정확도가 떨어진다. s(t)에 의해 크기가 조정된 프레임이 DNN 모델 m에 의해 처리될 때, [TeX:] $$C(s(t)) \in[0,1]$$를 정확도로 정의한다. [TeX:] $$C(s(t))$$는 concave하고 미분 가능하며, 증가하는 함수이다[14]. 또한, 모바일 비전 애플리케이션을 사용하기 위한 최소 시간 평균 정확도(임계값)를 [TeX:] $$c_{\mathrm{th}}$$로 정의한다. 2.3 단대단 지연 시간 모델단일 프레임을 처리하는 데 발생하는 단대단 지연 시간은 다음과 같이 네 가지로 구성된다. 1) 모바일 단말에서의 프로세싱 시간: i(t)에 따라 모바일 단말에서 처리해야 하는 GPU 사이클 수는 [TeX:] $$w s(t) \rho_{m, \mathrm{md}}^{i(t), s(t)}$$(cycles)이고, GPU 클럭 주파수는 [TeX:] $$g_{\mathrm{md}}$$ (cycles/second)으로 고정되어 있으므로, 모바일 단말 프로세싱에 걸리는 시간은 [TeX:] $$w s(t) \rho_{m, \mathrm{md}}^{i(t), s(t)} / g_{\mathrm{md}}$$(seconds)이다. 2) 중간 결과 업로드 시간: 모바일 단말에서 MEC 서버로 전송하는 데이터의 양은 [TeX:] $$w s(t) \sigma_{m, \mathrm{md}}^{i(t), s(t)}$$(bits)이고, 업링크 대역폭은 [TeX:] $$d(t)/\Delta t$$(bits/second)이므로 데이터 전송 시간은 [TeX:] $$w s(t) \sigma_{m, \mathrm{md}}^{j(t), s(t)} \Delta t / d(t)$$이다. 3) MEC 서버에서의 프로세싱 시간: MEC 서버에서 처리해야 하는 GPU 사이클 수는 [TeX:] $$w s(t) \rho_{m, \mathrm{es}}^{i(t), s(t)}$$ (cycles)이고, GPU 클럭 주파수는 [TeX:] $$g_{\mathrm{es}}$$(cycles/second)이므로 MEC 서버 프로세싱에 걸리는 시간은 [TeX:] $$w s(t) \rho_{m, \mathrm{es}}^{i(t), s(t)} / g_{\mathrm{es}}$$(seconds)이다. 4) 최종 결과 다운로드 시간: 비전 어플리케이션에서 최종 추론 결과(예: 이미지 내 물체에 대한 판단 결과)전송시간은 전체 추론시간 대비 매우 적은 비중을 차지하므로 최종 데이터 전송에 대한 시간은 생략한다. 따라서, 단대단 지연 시간 R(t)은 다음과 같다.
Ⅲ. 문제 정의 및 제안 알고리즘3.1 문제 생성본 모바일 비전 애플리케이션을 위한 QoE 개선 문제를 세운다. 우리의 목표는정확도와 단대단 지연시간을 충족하면서 처리 fps를 최적화하는 것이다. 먼저, 처리된 프레임과 입력 프레임의 시간 평균 비율 [TeX:] $$k(t)=\frac{a(t)}{b(t)}$$를 이용해 사용자의 만족도를 나타내는 유틸리티 함수 [TeX:] $$U(\cdot)$$를 정의한다. 유틸리티 함수는 concave 함수이며, 증가하고 미분 가능하다. 파티션 포인트 i(t), 처리 fps b(t), 크기 조정 팩터 s(t)를 동시에 제어하여 다음과 같이 fps 유틸리티를 최대화하는 문제를 정의한다.
[TeX:] $$\begin{gathered} (\mathrm{P} 1): \max _{i, b, s} U(\bar{k}), \\ \text { s.t. }\left\{\begin{array}{l} (C 1): \bar{R} \leq r_{t h} \\ (C 2): \overline{C(s)} \geq c_{t h} \\ (C 3): b(t) w s(t) \sigma_{m, \mathrm{md}}^{i(t), s(t)} \leq d(t), \forall t \in T, \\ (C 4): b(t) w s(t) \rho_{m, \mathrm{md}}^{i(t), s(t)} \leq g_{\mathrm{md}} \Delta \mathrm{t}, \forall \mathrm{t} \in T, \\ (\mathrm{C} 5): \mathrm{i}(\mathrm{t}) \in \mathrm{I}, \mathrm{~b}(\mathrm{t}) \in \mathrm{B}, \mathrm{~s}(\mathrm{t}) \in \mathrm{S} \end{array}\right. \end{gathered}$$ 여기서 (C1)과 (C2)는 각각 시간 평균 단대단 지연 시간과 정확도에 대한 제약 조건이다. (C3)은 업링크 전송에 필요한 데이터 양이 주어진 네트워크 대역폭을 초과할 수 없음을 나타낸다. (C4)는 모바일 처리에 필요한 GPU 사이클 양이 모바일 GPU의 처리 용량을 초과할 수 없음을 나타낸다. (C5)는 파티션 포인트 i(t), 처리 fps b(t), 크기 조정 팩터 s(t)의 선택 가능한 범위를 나타낸다. 시스템 상태 [TeX:] $$\Omega(t)=(a(t), d(t))$$는 독립항등분포(i.i.d.)이며, 타임슬롯마다 무작위로 변경된다. 또한, 알고리즘은 미래의 시스템 상태나 확률적 정보를 미리 알지 못한다고 가정한다. 유틸리티 함수 [TeX:] $$U(\cdot)$$는 시간 평균에 대해 비선형 함수이므로, 타임슬롯마다 문제를 풀어내기 어렵다. 따라서 (P1)을 타임슬롯마다 푸는 문제로 변환하기 위해 straight line set와 보조 변수를 추가한다. 먼저 임의의 상수 [TeX:] $$\left(x_{\min }, x_{\max }\right)$$로 이루어진 straight line set [TeX:] $$K=\left\{x \mid x_{\min } \leq x \leq x_{\max }\right\}$$을 정의한다. (P1)에 제약사항을 추가한 문제는 다음과 같다.
[TeX:] $$\begin{aligned} & \text { (P2): } \max _{i, b, s} U(\bar{k}), \\ & \text { s.t. } \quad\left\{\begin{array}{l} (C 1)-(C 5), \\ \bar{k} \in K . \end{array}\right. \end{aligned}$$ 이때 (P2)의 최대 유틸리티는 제약 조건으로 인해 (P1)보다 높을 수 없다. 그러나 집합 K의 범위를 충분히 넓게 설정하면 (P2)와 (P1)은 동일한 솔루션을 갖는다. 다음으로, (P2)를 시간 평균의 함수로 나타내기 위해 보조 변수 [TeX:] $$x(t) \in K$$를 소개한다. [TeX:] $$x(t)$$는 Jensen’s inequality로 인하여 다음과 같은 관계를 갖는다.
마지막으로, 보조 변수 [TeX:] $$x(t)$$를 추가하여 (P2)를 (P3)으로 변형한다.
[TeX:] $$\begin{aligned} & (\mathrm{P} 3): \quad \max _{i, b, s, x} \overline{U(x)} \\ & \text { s.t. }\left\{\begin{array}{l} (C 1)-(C 5), \\ (C b): \bar{x} \leq \bar{k}, \\ (C 7): x(t) \in K, \forall t \in T . \end{array}\right. \end{aligned}$$ 이때, [TeX:] $$x=\{x(t) \mid t \in T\}$$이며 보조 변수 [TeX:] $$x(t)$$는 입력 fps 대비 처리 fps에 대한 가상의 비율로, [TeX:] $$k(t)$$는 [TeX:] $$x(t)$$를 시간 평균 관점에서 따라간다. (P3)은 보조 변수 [TeX:] $$x(t)$$의 추가로 시간 평균 관점에서 풀 수 있는 문제이며, [TeX:] $$(i(t), b(t), s(t), \chi(t))$$를 동적으로 제어하여 유틸리티를 최대화하는 문제이다. (P3)의 목적함수의 최적값은 (P2)의 목적함수의 최적값과 같으며, (P2)의 목적함수의 최적값은 (P1)의 목적함수의 최적값과 같다. 3.2 알고리즘 유도먼저 유한 초기값 [TeX:] $$F(0), G(0), H(0)$$를 갖는 가상 큐 [TeX:] $$F(t), G(t), H(t)$$를 정의한다. [TeX:] $$(F(t), G(t), H(t))$$는 다음과 같이 정의된다.
만약 우리가 큐 [TeX:] $$(F(t), G(t), H(t))$$를 시간 평균 관점에서 안정화할 수 있다면, 제약 조건 (C1), (C2), (C6)이 충족 된다. 이제 가상 큐 [TeX:] $$(F(t), G(t), H(t))$$를 사용하여, Lyapunov drift 함수와 유틸리티 함수에 가중치 V를 곱한 합을 나타내는 Lyapunov drift-plus-penalty를 최 소화하는 알고리즘을 만들 수 있다. 3.3 알고리즘 설명이번 절에서는 딥러닝 모델 파티셔닝 알고리즘 Parecon을 제안한다. Parecon은 가상 큐 [TeX:] $$(F(t), G(t), H(t))$$, 입력 프레임의 수 a(t), 업링크 네트워크 자원 d(t)에 대한 정보들을 바탕으로 [TeX:] $$(x(t), i(t), b(t), s(t))$$를 결정한다. 1) 보조 변수 [TeX:] $$x(t)$$: 매 타임슬롯 t마다 가상의 큐 H(t)에 따라 Parecon은 다음 문제를 해결한다.
(7)[TeX:] $$\begin{aligned} & \min _{x(t)}-V U(x(t))+H(t) x(t), \\ & \text { s.t. }(C 7): x(t) \in K . \end{aligned}$$[TeX:] $$-V U(x(t)) \text { 는 } x(t)$$에 대해 convex하고, [TeX:] $$H(t) x(t) \text { 는 } x(t)$$에 대해 linear하기 때문에 식 (7)은 convex 함수이다. 또한 K는 straight line set이며 이는 convex set이다. 따라서, [TeX:] $$x(t)$$를 결정하는 것은 convex 최적화 문제이기 때문에, 최적의 [TeX:] $$x(t)$$는 다음과 같이 도출된다.
(8)[TeX:] $$x(t)=\left[\left(U^{\prime}\right)^{-1}\left(\frac{H(t)}{V}\right)\right]_{x_{\min }}^{x_{\max }}$$2) 그 외 변수 [TeX:] $$(i(t), b(t), s(t))$$: 매 타임슬롯 t마다 가상 큐 [TeX:] $$(F(t), G(t), H(t))$$에 따라 Parecon은 다음 문제를 해결한다.
(9)[TeX:] $$\begin{aligned} & \min _{i(t), b(t), s(t)}[\operatorname{IBS}(i(t), b(t), s(t)) \\ & =F(t)\left\{\frac{w s(t) \rho_{m, \mathrm{md}}^{i(t), s(t)}}{g_{\mathrm{md}}}+\frac{w s(t) \sigma_{m, \mathrm{md}}^{i(t), s(t)}}{d(t)} \Delta t+\frac{w s(t) \rho_{m, \mathrm{es}}^{i(t), s(t)}}{g_{\mathrm{es}}}\right\} \\ & \left.+G(t) C(s(t))-H(t) \frac{b(t)}{a(t)}\right] \\ & \text { s.t. }\left\{\begin{array}{l} (C 3): b(t) w s(t) \sigma_{m, \mathrm{md}}^{i(t), s(t)} \leq d(t), \\ (C A): b(t) w s(t) \rho_{m, \mathrm{md}}^{i(t), s(t)} \leq g_{\mathrm{md}} \Delta t, \\ (C 5): i(t) \in I, b(t) \in B, s(t)=S . \end{array}\right. \end{aligned}$$식 (9)에서 i(t), s(t)는 서로 결합되어 있으며, 제약 조건 (C3)과 (C4)에서 [TeX:] $$i(t), b(t), s(t)$$는 서로 결합 되어 있기 때문에 3개의 제어변수를 독립적으로 분할 할 수 없으며, 3차원 공간 내에서 솔루션 탐색을 수행해야 한다. 우선 Parecon 알고리즘의 검색 공간을 3차원에서 2차원으로 줄이기 위해 i(t), s(t)가 주어졌을 때 closed form으로 표현되는 최적의 처리 fps [TeX:] $$b_{i, s}(t)$$를 도출한다. 식 (9)는 i(t), s(t)가 주어질 때 다음과 같이 표현된다.
(10)[TeX:] $$\begin{gathered} \max _{b(t)} b(t), \\ \text { s.t. }\left\{\begin{array}{l} (\mathcal{C} 3): b(t) \leq \frac{d(t)}{w s \delta_{m, \mathrm{md}}^{i, s}}, \\ (C 4): b(t) \leq \frac{\mathrm{g}_{\mathrm{md}}^m \Delta \mathrm{t}}{w s \rho_{m, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}}} \\ (\mathrm{C} 5): \mathrm{b}(\mathrm{t}) \in\{0, \cdots, \mathrm{a}(\mathrm{t})\} . \end{array}\right. \end{gathered}$$이때 최적의 [TeX:] $$b_{i, s}(t)$$는 다음과 같이 구할 수 있다.
(11)[TeX:] $$b_{i, s}(t)=\min \left\lfloor\left[a(t), \frac{\mathrm{d}(\mathrm{t})}{w s \sigma_{m, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}}}, \frac{\mathrm{~g}_{\mathrm{md}} \Delta \mathrm{t}}{\mathrm{ws} \rho_{\mathrm{m}, \mathrm{md}}^{\mathrm{i}, \mathrm{~s}}}\right]\right\rfloor$$Parecon은 각 파티션 포인트 i(t)와 각 크기 조절 팩터 s(t)에 대한 반복을 기반으로 다음과 같이 [TeX:] $$(i(t), b(t), s(t))$$를 결정한다. 3.4 알고리즘 성능본 연구에서 제안한 알고리즘Parecon은 시간 평균 유틸리티에 대해 제약사항을 만족하면서 다음과 같은 성능을 보인다.
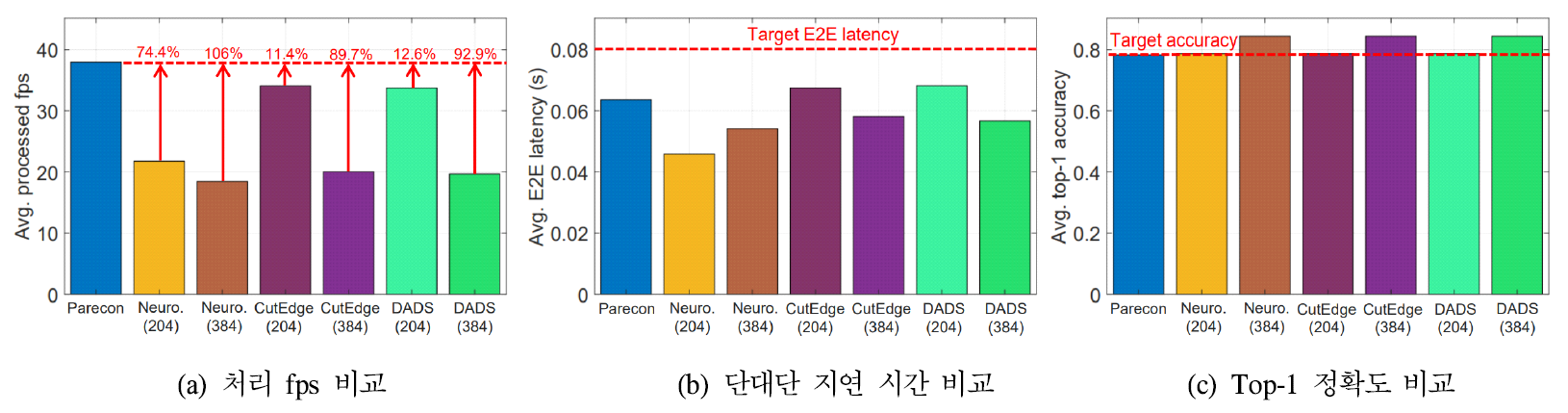
(12)[TeX:] $$\overline{U(x)} \geq \overline{U\left(x_{\mathrm{P} 3}^*\right)}-\frac{\mathrm{B}}{\mathrm{~V}}r$$여기서 [TeX:] $$\overline{U\left(x_{\mathrm{P} 3}^*\right)}$$는 (P3)을 풀어 얻을 수 있는 유틸리티의 최대값이다. 이때 B는 상수이며, 가중치 V를 증가시킬수록 최적의 유틸리티에 더욱 근접할 수 있다. Ⅳ. 시뮬레이션 기반 평가4.1 시뮬레이션 환경본 시뮬레이션에서는 모바일 기기의 사용자가 이미지 분류 비전 애플리케이션을 사용하는 환경을 가정한다. 딥러닝 모델은 Pytorch를 기반으로 사전 훈련된 EffcientNetV2-S[16]이고, 모델을 9개의 레이어 그룹으로 나눈다. 입력되는 프레임의 수는 30~60개 범위에서 타임슬롯마다 무작위로 생성되며, 모바일 단말의 GPU 클럭 주파수는 NVIDIA Jetson NX Xavier 보드를 기준으로 956MHz로 설정하고, MEC 서버의 GPU 주파수는 RTX4090의 스펙으로 설정한다. 업링크 네트워크로 보낼 수 있는 데이터의 양은 6.68Mbps~66.76Mbps 범위에서 타임슬롯마다 변동하며, 각 타임슬롯의 간격은 1초, 전체 타임슬롯 수는 1500으로 설정한다. 가중치 파라미터 V는 세 가지 QoE 지표 사이에 좋은 균형을 갖는 지점을 실험적으로 찾았으며 20으로 설정한다. 4.2 시뮬레이션 결과그림 3은 Parecon의 top-1 정확도, 처리 fps 및 단대단 지연 시간을 나타낸다. 즉, top-1 정확도의 요구사항 [TeX:] $$c_{\mathrm{th}}$$를 변화시켜가며 얻어지는 처리 fps (processed fps)와 단대단 지연 시간(E2E latency)의 변화를 측정한 것이다. 요구 정확도가 작아질수록 알고리즘은 fps를 높이는 데 더 집중하며, 자연스럽게 fps는 높아지고 정확도는 낮아진다. 또한, 대부분의 상황에서 처리 fps가 높아지면 단대단지연 시간은 감소한다. 반대로 요구정확도가 높아질수록 알고리즘은 fps가 조금 줄어들더라도 정확도를 높이는 데 집중하며, 자연스럽게 처리 fps는 낮아지고 단대단 지연 시간은 증가한다. 그림(Fig.) 3. 요구 정확도 값에 따른 처리 fps, 단대단 지연 시간, top-1 정확도. (Processed FPS, E2E latency, and top-1 accuracy based on the required accuracy value.) 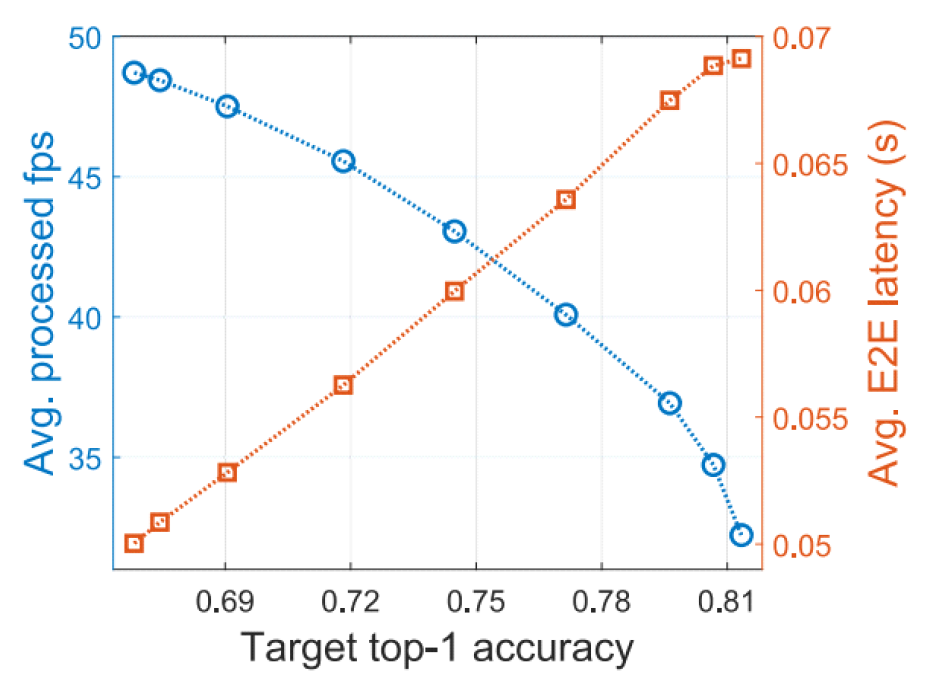 그림 4는 단대단 지연 요구사항 [TeX:] $$r_{\mathrm{th}}$$를 0.08초로, 정확도 요구사항 [TeX:] $$c_{\mathrm{th}}$$을 0.78로 설정할 때, 기존 알고리즘과의 QoE 비교 결과를 보여준다. Neurosurgeon은 파이프라인 없이 지연 시간만을 최소화하고[9], DADS는 파이프라인 환경에서 상황에 따라 처리 fps 또는 지연 시간 중 하나만을 최적화한다[13]. CutEdge는 파이프라인 환경에서 모델 파티셔닝을 수행하여 처리 fps와 지연 시간을 동시에 최적화하지만, 입력 프레임의 크기는 별도로 조절하지 않는다[15]. 여기서 정밀한 비교를 위해 비교 알고리즘 별 입력 프레임 크기를 2개씩 테스트한다. 먼저 Neurosurgoen은 파이프라인을 사용하지 않기 때문에 추가적인 지연 오버헤드가 없고, 지연 시간 최소화에만 집중하기 때문에 가장 낮은 지연 시간을 갖지만, 높은 처리 fps를 갖는 건 불가능하다. 다음으로 CutEdge는 204*204 프레임 크기에서 Neurosurgoen보다 높은 처리 fps를 달성하는데, 이는 파이프라인을 활용함과 동시에 처리 fps와 지연 시간을 함게 고려하기 때문이다. 하지만CutEdge는 시스템 상태 변화에 따라 입력 프레임 크기를 동적으로 조절할 수 없기 때문에 Parecon보다 낮은 처리 fps와 더 높은 지연시간을 보인다. 한편 DADS는 상황에 따라 처리 fps와 지연 시간 중 하나의 QoE 지표만을 고려하기 때문에 CutEdge와 유사하지만 약간 낮은 성능을 보인다. 마지막으로, Parecon은 DNN 모델 파티셔닝과 함께 입력 프레임 크기를 유연하게 조정함으로써 요구 사항을 충족하면서도 가장 높은 처리 fps를 달성한다. Ⅴ. 결 론모바일 비전 애플리케이션 사용자의 경험 품질은 애플리케이션의 정확도, 하나의 프레임의 처리 시간을 나타내는 단대단 지연 시간, 처리 속도를 나타내는 처리 fps에 큰 영향을 받는다. 본 연구에서는 모바일 비전 애플리케이션 사용자 경험 품질 향상을 위한 딥러닝 모델 파티셔닝 기반 제어 알고리즘을 제안한다. 이는 모델 파티션 포인트, 처리할 프레임의 수, 입력 프레임의 크기를 제어하며, 최대 단대단 지연 시간 및 최소 top-1 정확도를 보장하며 fps 유틸리티를 증가시킨다. 시뮬레이션을 통해 제안하는 알고리즘이 요구된 정확도에 따라서 처리 fps, 정확도 및 단대단 지연 시간이 달라진다는 것을 확인했다. 또한, 기존에 제안되었던 딥러닝 모델 파티셔닝 알고리즘과 비교하여 사용자 경험 품질 개선에 높은 효과가 있음을 검증하였다. BiographyBiographyReferences
|
StatisticsCite this articleIEEE StyleJ. Park and Y. Kim, "DNN Model Partition and Resolution Control for Edge-Assisted Mobile Vision AI," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 8, pp. 1256-1264, 2025. DOI: 10.7840/kics.2025.50.8.1256.
ACM Style Junsoo Park and Yeongjin Kim. 2025. DNN Model Partition and Resolution Control for Edge-Assisted Mobile Vision AI. The Journal of Korean Institute of Communications and Information Sciences, 50, 8, (2025), 1256-1264. DOI: 10.7840/kics.2025.50.8.1256.
KICS Style Junsoo Park and Yeongjin Kim, "DNN Model Partition and Resolution Control for Edge-Assisted Mobile Vision AI," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 8, pp. 1256-1264, 8. 2025. (https://doi.org/10.7840/kics.2025.50.8.1256)
|