IndexFiguresTables |
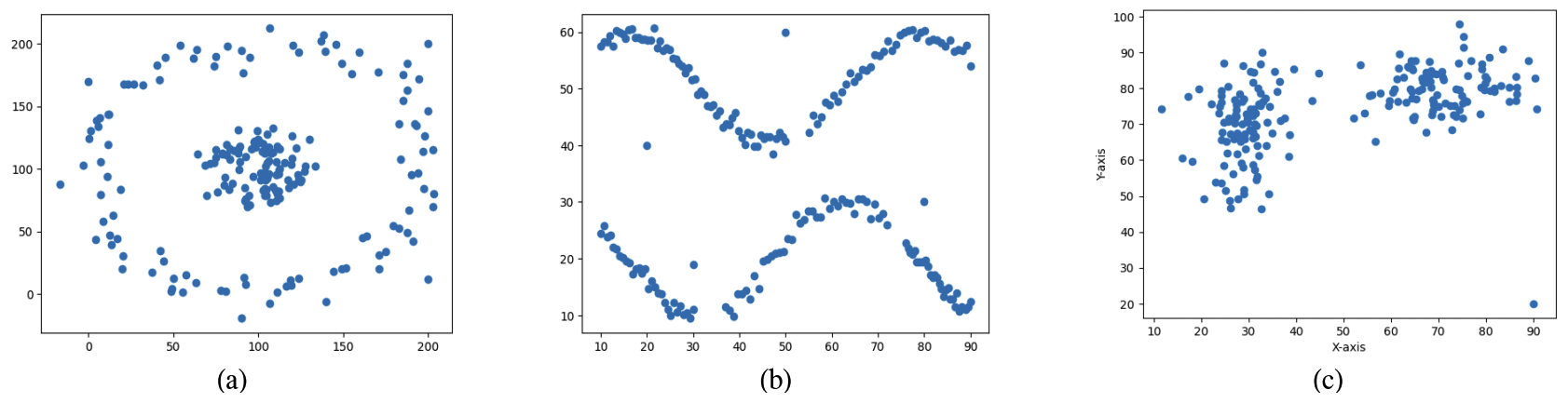
Jongkwan Lee♦ and Minwoo Lee°Task Allocation Scheme for Unmanned Systems Using Density-Based Clustering in Tactical Mission EnvironmentsAbstract: In this paper, we propose a scheme for efficiently assigning mission points to unmanned systems in a tactical environment where multiple unmanned systems are required to traverse a large number of differently distributed mission points. The proposed scheme consists of three steps. In step 1, the mission points are clustered based on density. In step 2, the number of clusters formed in step 1 and the number of available UAVsare consideredtosplit orconsolidatethe clusters.Instep 3,consolidatemissionpoints thatweretreated as noise during density-based clustering into neighboring clusters. By clustering the mission points in stages, it improves the mobility efficiency of the unmanned systems and avoids the concentration of missions on specific unmanned system through the cluster splitting and consolidation process. Through experiments under various mission point placement conditions, it is verified that the proposed scheme not only reduces the total travel time of unmanned systems compared to the k-means clustering-based mission assignment method, but also enables balanced mission assignment to avoid the concentration of mission points on a particular unmanned system in terms of travel time. Keywords: task alocation , clustering , unmanned systems , tactical environment 이종관♦, 이민우°전술 임무환경에서 밀도 기반 클러스터링을 이용한 무인체계 임무 할당 기법요 약: 본 논문은 다수의 무인체계가 다양한 형태로 분포된 임무지점들을 순회해야 하는 상황에서 임무지점을 무인체계에게 효과적으로 할당하는 기법을 제안한다. 제안하는 기법은 3단계로 구성된다. 1단계에서는 임무지점들을 밀도 기반으로 클러스터링한다. 2단계에서는 1단계에서 형성된 클러스터의 수와 가용한 무인체계의 수를 고려하여클러스터를 분할 또는 통합한다. 3단계에서는 밀도 기반 클러스터링 과정에서 노이즈로 처리된 임무지점을 인근클러스터로 통합한다. 임무지점들을 단계적으로 클러스터링함으로써 무인체계의 이동 효율성을 향상시키고 클러스터 분할과 통합 과정을 통해 특정 무인체계에 임무가 집중되는 것을 방지한다. 다양한 임무지점 배치 조건에서의실험을 통해 제안하는 기법이 k-means 클러스터링 기반의 임무할당 기법에 비해 무인체계들의 총 순회시간을 단축할 뿐 아니라 특정 무인체계에 임무지점이 집중되지 않도록 균형된 임무할당이 가능함을 확인하였다. 키워드: 임무할당, 군집화, 무인체계, 전술환경 Ⅰ. 서 론많은 군사전문가들은 지속적인 병력감소, 작전 지역의 확대, 과학기술의 급속한 발전 등으로 무인체계가 미래 전장에서 적극적으로 활용될 것으로 예상하고 있다. 작전 환경의 변화, 작전 유형 및 목적 그리고 무인체계의 상태에 따라 임무를 개별 무인체계들에 적절히 할당하는 것은 무인체계의 효율적 운용과 임무 달성 측면에서 중요하고 어려운 문제이다. 실시간으로 변화하는 복잡한 전장환경에서 무인체계에 임무를 효과적으로 할당하기 위해서는 여러 가지 변수들을 동시에 고려해야 한다. 뿐만 아니라 전장 환경에 대한 높은 이해도와 신속한 의사결정이 요구된다. 따라서 임무할당 오류와 비효율성이 초래되기 쉽다.[1-3] 이러한 문제를 해결하기 위한 일반적인 방법은 유사한 특성을 갖는 임무들을 하나의 군집으로 정의하고 해당 군집(즉, 임무 모음)을 개별 무인체계에 할당하는 것이다. 제안하는 기법은 다수의 임무지점을 개별 무인체계에게 할당하기 위해 밀도 기반 클러스터링 기법인 DBSCAN(Density Based Spatial Clustering of Applications with Noise)과 k-means 알고리즘을 사용한다. DBSCAN은 밀도 기반 클러스터링으로 데이터 포인트 간의 밀도에 따라 클러스터를 형성한다. 기본적으로 특정거리 내에서 최소 개수의 데이터 포인트가 존재하는 지역을 클러스터로 정의하고 밀도가 낮은 지역의 포인트들을 노이즈로 처리한다. DBSCAN은 클러스터의 수를 미리 설정할 필요가 없고 원형이 아닌 복잡한 형태의 클러스터도 잘 식별한다. 또한 밀도가 낮은 데이터를 노이즈로 분리할 수 있어 이상치(outlier)나 노이즈가 포함된 데이터셋에서도 유용하다. 하지만 알고리즘에 적용되는 파라미터에 따라 성능 민감성이 크고, 데이터셋이 크면 각 데이터 포인트에 대해 이웃 포인트를 계산하는데 시간이 많이 걸려 계산 속도 문제를 야기할 수 있다.[5,6] k-means 알고리즘은 데이터를 k개의 클러스터로 나누는데 초기 중심점을 선택하고, 각 데이터 포인트를 가장 가까운 중심점에 할당한 후, 각 클러스터의 평균을 계산하여 중심점을 반복적으로 갱신하는 방식으로 동작한다. 알고리즘이 단순하여 클러스터링 결과에 대한 이해와 해석이 쉽고, 계산량이 적어 대규모 데이터에서도 잘 동작한다. 하지만 k 값을 사전에 선정해야 하고, 초기값에 따라 최종 결과가 달라질 수 있다. 그리고 클러스터가 원형이고 데이터 밀도가 균일한 경우 잘 동작하지만, 복합한 모양의 클러스터나 밀도가 균일하지 않은 데이터에서는 성능이 저하된다. 또한 이상치나 노이즈가 클러스터 중심에 큰 영향을 미칠 수 있다는 단점이있다.[4,10] 제안하는 기법은 DBSCAN과 k-means의 단점을 배제하고 장점을 활용하기 위해 이들을 단계적으로 조합한 형태이다. 제안하는 기법은 DBSCAN을 통해 밀도 기반으로 임무 지점들을 1차적으로 클러스터링한 후 클러스터의 규모, 가용 무인체계의 수 그리고 임무 지점까지의 이동거리 등을 고려하여 클러스터를 분할 또는 병합한다. 클러스터를 분할할 때에는 k-menas 알고리즘이 사용된다. 그리고 밀도 기반 클러스터링 과정에서 노이즈로 처리된 임무지점을 인근 클러스터에 포함시킨다. 그리고 최종적으로 각 클러스터를 무인체계에 할당한다. 본 논문의 구성은 다음과 같다. 2장에서 관련 연구에 대해서 간략히 살펴보고 3장에서 시스템 모델과 가정사항 그리고 해결하고자 하는 문제를 정의한다. 4장에서 제안하는 기법에 대해 구체적으로 설명하고 5장에서 제안하는 기법의 성능을 실험적으로 분석한다. 마지막으로 6장에서 결론을 맺는다. Ⅱ. 관련 연구클러스터링은 데이터를 유사한 특성을 가진 그룹으로 나누는 비지도 학습 기법으로 데이터의 패턴과 구조를 기반으로 클러스터를 찾아낸다. 대표적인 클러스터링 알고리즘에는 k-means 클러스터링, DBSCAN, Mean Shift, 계층적 클러스터링, GMM(Gaussian Mixture Model) 등이 있다. 클러스터링 알고리즘들은 각각의 특성과 장단점을 가지고 있다. 앞서 설명한 DBSCAN과 k-means 이외의 클러스터링 기법에 대한 특징 및 장단점에 대해 설명한다. Mean Shift는 DBSCAN과 같이 밀도 기반 클러스터링 기법으로 클러스터 개수를 사전에 설정할 필요가 없으며, 데이터 밀도에 따라 다양한 형태의 클러스터를 효과적으로 탐지할 수 있고 이상치에도 강건한 특성을 가진다. 하지만 반복적 계산으로 대규모 데이터에서는 연산이 느릴 수 있고, 매개변수 설정에 따라 성능이 크게 좌우되며, 고차원 데이터에서는 밀도 추정 정확도가 떨어진다. 따라서 Mean Shift의 효과적인 사용을 위해서는 데이터 특성에 맞는 신중한 파라미터 조정이 필수적이다.[7] 계층적 클러스터링은 클러스터의 계층 구조를 구축하는 기법으로 클러스터의 병합 또는 분할을 시각화하는 덴드로그램을 생성한다. 군집 개수를 미리 선정할 필요가 없고 계층 관계에 대한 명확하고 해서 가능한 시각적 표현을 제공한다. 하지만, 높은 시간 복잡도로 대규모 데이터셋에 적합하지 않고 노이즈에 민감한 단점이 있다.[8] GMM은 복잡한 데이터 구조를 모델링할 수 있는 강력하고 유연한 클러스터링 기술이다. 클러스터의 모양과 밀도가 다르거나 확률적 할당이 필요한 경우 유용하다. 하지만 초기 조건에 민감할 수 있고 많은 계산량이 요구된다. 또한, 클러스터 내의 데이터들이 가우스 분포를 따른다고 가정하기 때문에 이 가정에 부합하지 않을 때에는 성능이 좋지 않을 수 있다.[9] 한편, 클러스터링 기반 임무할당 기법은 일반적으로 임무들간의 상관관계와 임무를 수행할 무인체계의 수를 고려하여 임무들을 클러스터링하고 각 클러스터를 무인체계에 할당한다. 클러스터링 기법을 활용한 무인체계의 임무할당과 관련한 대표적인 연구결과는 아래와 같다. F. Meng 외 5인은 대규모 다중 로봇 임무 할당 문제에서 통신 빈도와 계산 복잡도를 줄이기 위해 클러스터링 기반의 임무 할당 알고리즘을 제안하였다.[11] k-means++ 알고리즘으로 임무와 로봇을 그룹화하여 대규모 문제를 소규모 문제로 나누었고, 각 그룹 내에서 독립적으로 Consensus-Based Bundle Algorithm (CBBA)를 적용하여 임무를 할당하였다. 그룹화를 통해 통신 빈도를 감소하였고 그룹별 병렬 처리로 임무할당 시간을 단축하였다. 하지만 그룹별 임무의 수와 로봇의 수가 불균형할 때 리소스가 낭비되거나 부족할 수 있고 동적인 환경에서 그룹 재구성이 어려울 수 있다. 또한 k-means++ 알고리즘의 초기 클러스터 중심 설정이 전체 성능에 영향을 미칠 수 있다. B. Fei 외 5인은 도시 환경에서의 화물 배송을 위한 다중 UAV의 동적 임무 할당 문제를 해결하기 위해 SC(Spectral Clustering)와 PSO(Particle Swarm Optimization)을 결합한 방법을 제안하였다.[12] SC로 임무를 그룹화하고, PSO를 통해 임무 우선순위를 최적화해 UAV의 에너지 소비와 임무 수행시간을 감소시킨다. 효율적인 임무 그룹화가 가능하고 UAV의 에너지 소모로 인한 임무 중단 상황을 실시간적으로 처리하여 임무 성공률을 향상시킬 수 있다. 하지만 SC와 PSO의 결합으로 계산 복잡도가 높으며, SC의 초기 설정에 따라 임무할당의 결과가 크게 달라질 수 있다. Z. Junwei 외 1인은 다수 UAV가 협력하여 다중 목표 지점을 정찰하는 문제를 해결하기 위해 K-means 클러스터링 알고리즘과 시뮬레이티드 어닐링(simulated annealing) 알고리즘을 결합한 기법을 제안하였다.[13] k-means 클러스터링을 통해 UAV 그룹 간의 임무를 균형되게 할당하고 시뮬레이티드 어닐링으로 UAV들의 비행경로를 최적화하여 총 비행시간을 단축시킨다. 하지만 k-means 클러스터링 기반의 기법이기 때문에 클러스터 수를 사전에 정의해야 하고, 초기 중심값에 따라 결과가 크게 달라질 수 있다. 특히, 임무지점들이 비균형적인 분포 또는 비구형(non-spherical) 분포인 경우에는 효과적인 클러스터링, 즉 임무할당이 제한된다. W. Tian 외 3인은 이기종 UAV들이 특정 순서대로 다중 임무지점에서 여러 임무를 수행해야 하는 상황에서 UAV가 앞선 임무가 완료되기 전까지 임무지점에서 대기해야 하는 교착(deadlock) 문제를 해결하기 위한 기법을 제안하였다.[14] 제안한 기법은 UAV 위치를 기준으로 임무지점을 클러스터링하여 임무지점을 순회하는 순서를 정의하고, BPSO(Bidirectional ParticleSwarm Optimization)를 통해 임무지점 순회 순서와 UAV 배정을 동시에 최적화한다. 이를 위해 UAV간의 최대 작업시간과 총 작업 시간을 최소화하는 것을 목표로 하는 비용함수로 정의하였다. 클러스터링은[13]에서 제안한 기법을 적용하였다. 따라서 클러스터링 관점에서 [3]에서 제안한 기법의 단점과 문제점을 동일하게 갖고 있다. 클러스터링 기반의 임무할당 기법들은 분류 대상 임무가 불균형할 때 효과적으로 동작하지 못하고, 초기 조건에 대한 민감성이 높은 문제점이 있다. Ⅲ. 시스템 모델 및 문제 정의이번 장에서는 본 논문이 고려하는 시스템 모델과 가정사항 그리고 해결하고자 하는 문제를 정의한다. 3.1 시스템 모델 및 가정사항본 논문에서는 다수의 임무지점을 다수의 무인체계를 이용하여 방문하는 상황을 가정한다. 무인체계가 수행하는 임무는 임무지점에 대한 단순한 탐색일 수도 있고, 임무지점에 전장센서들이 설치되어 있어 센서 데이터를 수집하는 것일 수도 있다. 무인체계가 각 임무지점에 도착해 해당 임무를 완료하는데 걸리는 시간은 동일하다고 가정한다. 작전 지역에는 NT개의 임무지점이 존재하며, NU개의 무인체계가 존재한다. T는 임무지점의 집합이며, U는 무인체계의 집합이다.
(1)[TeX:] $$\begin{equation}T=\left\{t_1, t_2, \ldots, t_i, \ldots, t_{N_t}\right\}\end{equation}$$
(2)[TeX:] $$\begin{equation}U=\left\{u_1, u_2, \ldots, u_j, \ldots, u_{N_u}\right\}\end{equation}$$위 식에서 ti는 i번째 임무지점을 나타내며, uj는 j번째 무인체계를 나타낸다. 이때, 임무지점의 수는 무인체계의 수보다 많다. 본 논문에서는 임무지점을 정점(vertex)으로 하고, 임무지점 간의 엣지(edge)를 무인체계가 이동하는 경로로 나타내는 유향 그래프(directed graph)로 모델링한다. 그리고 엣지 지연시간(d)은 무인체계가 임무지점 사이의 경로를 이동하는데 소요되는 시간으로 정의한다. [TeX:] $$\begin{equation}d_{i, j}^k\end{equation}$$는 무인체계 uk가 임무지점 ti에서 임무지점 tj로 이동하는데 걸리는 시간을 나타낸다. 그리고 임무할당 정책 ϕ에 의해서 무인체계 uk에 할당된 임무지점 집합 [TeX:] $$\begin{equation}T_\phi^k\end{equation}$$과 무인체계 uk가 할당받은 임무지점을 방문하는 순서 [TeX:] $$\begin{equation}P_\phi^k\end{equation}$$는 각각 아래와 같이 표기한다.
(3)[TeX:] $$\begin{equation}T_\phi^k=\left\{t_{\phi, 1}^k, t_{\phi, 2}^k, \ldots, t_{\phi, N_k^b}^k\right\}, k=0,1, \ldots, N_U\end{equation}$$
(4)[TeX:] $$\begin{equation}P_\phi^k=\left[p_{\phi, 1}^k, p_{\phi, 2}^k, \ldots, p_{\phi, N_k^k}^k\right], k=1,2, \ldots, N_U\end{equation}$$식 (3), (4)에서 [TeX:] $$\begin{equation}N_k^{\mathrm{N}}\end{equation}$$는 임무할당 정책 ϕ를 적용했을 때 무인체계 uk에 할당된 임무지점의 수를 나타낸다. 그리고 [TeX:] $$\begin{equation}T_\phi^0\end{equation}$$은 어떤 무인체계에도 할당되지 않은 임무지점의 집합이다. 3.2 문제 정의본 논문에서 해결하고자 하는 문제는 다수의 무인체계에 다수의 임무를 할당할 때 무인체계들이 임무수행을 위해 이동해야 하는 시간을 최소화하면서 무인체계 별로 임무를 최대한 형평성있게 할당하는 것이다. 따라서, 아래와 같은 목적함수와 제약조건을 정의한다.
(5)[TeX:] $$\begin{equation}\min _{\phi \in \mathscr{D}}\left(\alpha \cdot f_\phi-\beta \cdot d_\phi\right)\end{equation}$$
(6)[TeX:] $$\begin{equation}\text { s.t. } \sum_{k=1}^{N_U} N_k^\phi=N_T, \forall \phi \in \Phi\end{equation}$$
(7)[TeX:] $$\begin{equation}T_\phi^i \cap T_\phi^j=\varnothing, \forall u_i, u_j \in U\end{equation}$$
(8)[TeX:] $$\begin{equation}p_i^\phi \neq p_j^\phi, \forall p_i^\phi, p_j^\phi \in P_\phi^k\end{equation}$$식 (5)에서 [TeX:] $$\begin{equation}f_\phi, d_\phi\end{equation}$$는 정책 ϕ에 의해서 임무가 할당되었을 때 무인체계들의 임무할당 형평성과 임무수행을 위한 이동시간을 나타낸다. 식 (5)는 무인체계들의 이동 소요시간이 최소화되고 무인체계들이 수행해야 하는 임무의 양이 서로 최대한 유사해야 한다는 의미이다. α와 β는 형평성과 이동시간의 중요도에 따라 선택되는 가중치이다. 식 (6)은 무인체계에 할당된 임무지점의 합이 전체 임무수행 수와 같아야 한다는 조건이다. 식(7)은 임무지점이 다수의 무인체계에 할당되지 않고 오직 한 개 무인체계에만 할당되는 조건이다. 그리고 식(8)은 무인체계가 임무수행을 위해 이동할 때 동일한 임무지점을 반복하여 경유하지 않는다는 조건이다. Ⅳ. 제안하는 임무할당 기법본 장에서는 3장에서 정의한 문제를 해결하기 위해 제안하는 임무할당 기법을 구체적으로 설명한다. 제안하는 기법은 크게 3단계로 구성된다. 1단계는 임무지점을 밀도 기반으로 클러스터링하는 단계이다. 2단계는 1차 클러스터링 결과를 바탕으로 클러스터를 분할 또는 병합하는 단계이다. 3단계는 1, 2단계에서 클러스터에 할당되지 않은 임무지점들을 처리하는 단계이다. 4.1 1단계 : 밀도 기반 클러스터링1단계는 밀도 기반으로 임무지점을 클러스터링하는 단계이다. 이를 위해 제안하는 기법에서는 DBSCAN을 적용한다. DBSCAN는 2개의 인자를 필요로 한다. 하나는 특정 임무지점으로 부터의 거리 이고, 다른 하나는 반경 내에 있는 임무지점의 수인 minPts이다. 이 작고 minPts가 클수록 높은 밀도의 클러스터를 형성하고, 이 크고 minPts가 작을수록 낮은 밀도의 클러스터를 형성한다. 인자값의 선택에 따라서 클러스터링 결과가 크게 달라진다. 또한, 클러스터에 포함되지 않는 임무지점이 발생할 수 있다. 클러스터링을 수행했을 때 클러스터의 수(NC)와 무인체계의 수(NU)의 비율에 따라 과 minPts이 조정된다. NC가 NU에 비해 과도하게 크면 를 증가시키고 minPts을 감소시킨다. 반대로 NC가 NU에 비해 과도하게 작으면 를 감소시키고 minPts을 증가시킨다. 이러한 과정을 아래 조건을 만족할 때까지 반복한다.
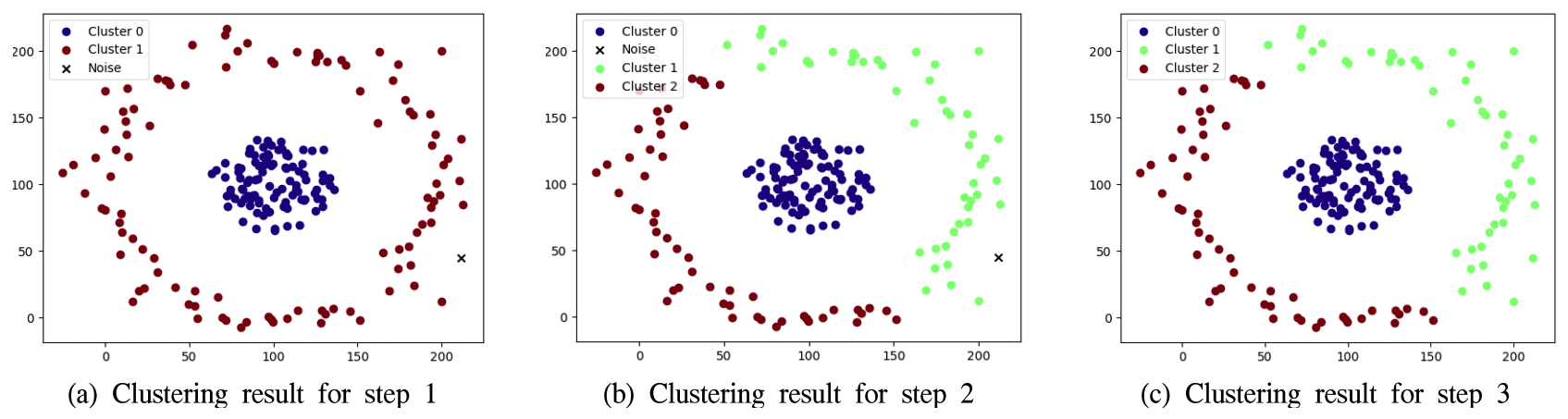
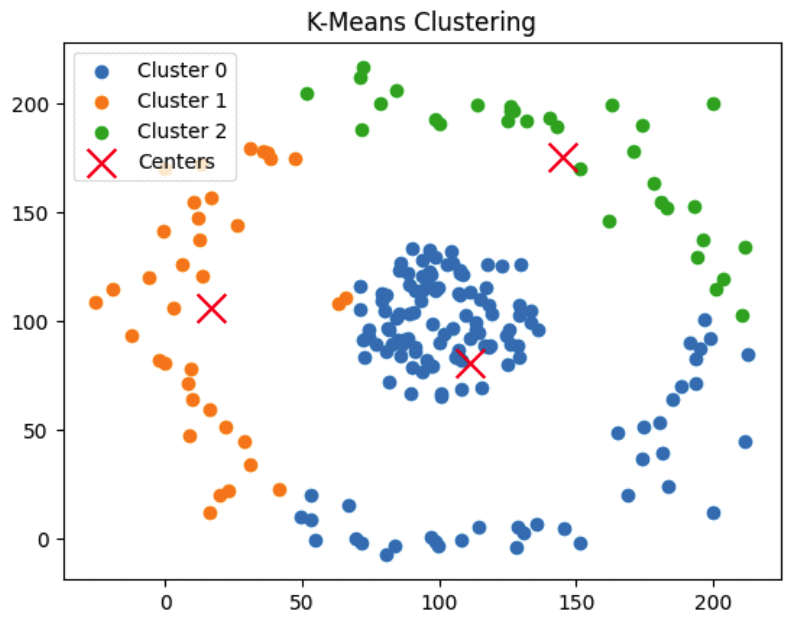
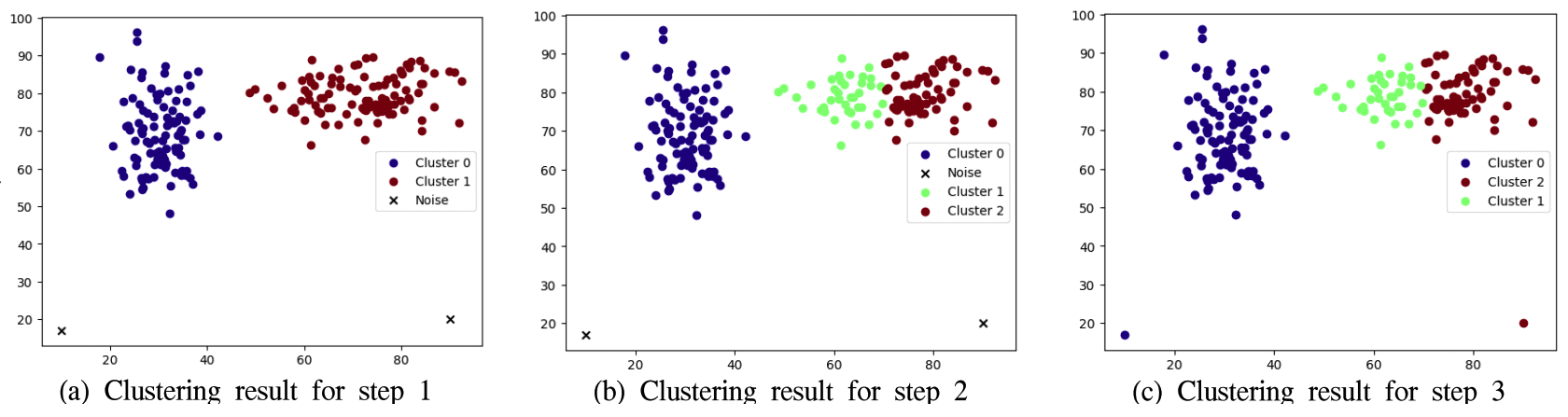
위 식에서 γ1, γ2는 NC와 NU의 비율을 결정하는 파라미터이다. DBSCAN의 계산복잡도는 Spatial Indexing을 사용했을 때 O(nlogn)이다. 고차원 데이터 또는 수 백만개의 데이터 포인터에 대해서는 성능이 크게 저하된다. 하지만 본 논문에서 가정한 전술상황에서 임무지점은 저차원 데이터이고 임무지점의 수가 현실적으로 수 백만 개가 되지 않는다. 따라서 DBSCAN이 제안하는 기법의 성능을 저하시키지 않는다. 4.2 2단계 : 클러스터 분할 또는 병합2단계에서는 1단계에서 수행한 클러스터링 결과에 따라 클러스터 분할 또는 병합을 수행한다. 클러스터의 분할 및 병합은 클러스터의 수(NC)와 무인체계의 수(NU)에 따라 아래와 같이 처리된다. 그리고 클러스터에 속한 임무지점을 무인체계가 순회하는 시간이 고려된다. · NC = NU : 별도의 조치 없이 3단계로 넘어간다. · NC > NU : 클러스터를 병합한다. 클러스터에 속한 임무지점을 순회하는 시간이 가장 적은 클러스터들을 NC = NU 조건이 될 때까지 반복적으로 병합한다. · NC < NU : 클러스터를 분할한다. 클러스터에 속한 임무지점을 순회하는 시간이 가장 큰 클러스터를 k-means 알고리즘을 이용하여 분할한다. 이때 k값은 2로 설정된다. 그리고 NC = NU 조건이 될 때까지 반복한다. 2단계에서 수행되는 k-means는 1단계에서 DBSCAN이 적용되어 밀도가 비교적 균일한 클러스터들을 대상으로 수행된다. 따라서 k-means에 의한 분할 성능이 우수한다. 4.3 3단계 : 노이즈 처리2단계를 마치면 어떤 클러스터에도 속하지 않은 임무지점들이 존재할 수 있다. 이들은 DBSCAN에 의해 클러스터링되지 않는 노이즈로 취급된다. 3단계에서는 이들을 [TeX:] $$\begin{equation}T_\phi^0\end{equation}$$에 속하지 않은 임무지점들 중에서 가장 근거리에 있는 임무지점이 속한 클러스터로 각각 할당한다. 만약 [TeX:] $$\begin{equation}T_\phi^0=\varnothing\end{equation}$$이라면 별도의 조치없이 종료된다. Ⅴ. 성능 분석본 장에서는 제안하는 기법의 성능을 3가지 실험 시나리오에 기반하여 분석한다. 5.1 실험 시나리오임무지점은 200개이고 무인체계는 3개이다. 그리고 무인체계는 모두 (0, 0) 지점에 위치하며, 임무지점을 순회하고 원위치로 돌아온다. 실험 시나리오는 임무지점 배치 유형에 따라 3가지로 구분한다. 첫 번째 시나리오는 임무지점들이 2개의 원형을 형성하며, 작은 원형이 큰 원형 안에 존재하는 형태이다. 두 번째 시나리오는 임무지점들이 2개의 곡선을 형성하는 형태이다. 마지막 3번째 시나리오는 임무지점들이 2개의 군집을 형성하고 다수의 이상치가 존재하는 형태이다. 그림 1은 각 시나리오별 임무지점들의 배치 형태를 나타낸다. 임무지점들을 클러스터링하고 각 클러스터에 속한 임무지점들은 각각 무인체계에 할당된다. 그리고 무인체계의 임무는 할당된 임무지점을 순회하고 최초 위치로 되돌아오는 것이다. 이때, 임무지점 순회를 위한경 로는 계산량을 고려하여 동적계획법을 이용하여 설정한다. 5.2 시나리오 1 : 이중 원형 배치첫 번째 시나리오는 그림 1의(a)에서 보는 바와 같이 임무지점들이 이중 원형으로 배치된 경우이다. 그림 2는 제안하는 기법이 적용되었을 때 각 단계별 클러스터링 상태를 나타낸다. 1단계가 종료되었을 때 4개의 클러스터링이 형성된다. 그리고 1개의 임무지점이 어느 클러스터에도 속하지 않아 노이즈로 처리된다. 2단계에서는 무인체계의 수가 클러스터 수보다 적기 때문에 (즉, NC > NU) 클러스터 병합이 이루어진다. 마지막으로 3단계에서 노이즈로 처리된 임무지점이 가장 근거리에 있는 클러스터에 할당되었다. 한편, 그림 3은 동일한 조건에서 k-means 알고리즘을 적용한 결과이다. 가운데 몰려있는 임무지점들이 하나의 무인체계에 할당되지 않고 여러 무인체계들에게 비효율적으로 할당되는 것을 알 수 있다. 이는 k-means 알고리즘이 임무지점들의 밀도를 고려하지 않고 클러스터의 중심점과 임무지점들간의 거리만을 고려하여 임무를 할당하기 때문이다. 표 1은 제안하는 기법과 k-means 알고리즘을 적용했을 때 각각의 무인체계별 순회거리와 FI(fairness index)를 나타낸다. k-means 알고리즘을 적용했을 때보다 제안하는 기법을 적용했을 때 무인체계들의 순회거리가 짧고 FI가 크다. 이는 제안하는 기법이 특정 무인체계에 집중되지 않게 임무를 균형되고 효과적으로 할당함을 의미한다. 표 1. 무인체계들의 순회거리 및 형평성 지표 (시나리오 1)
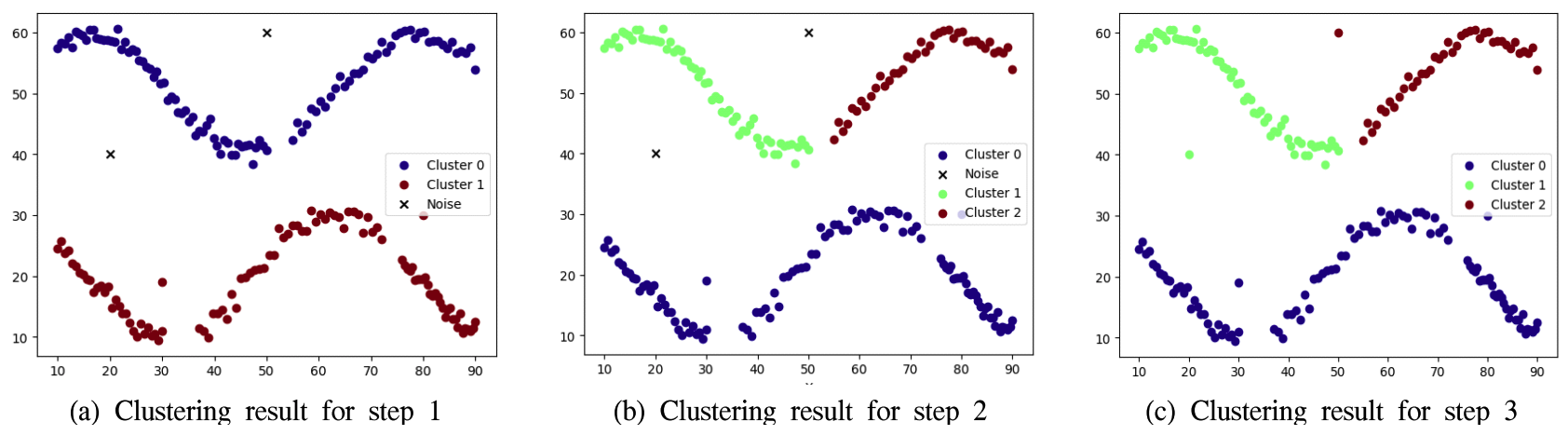
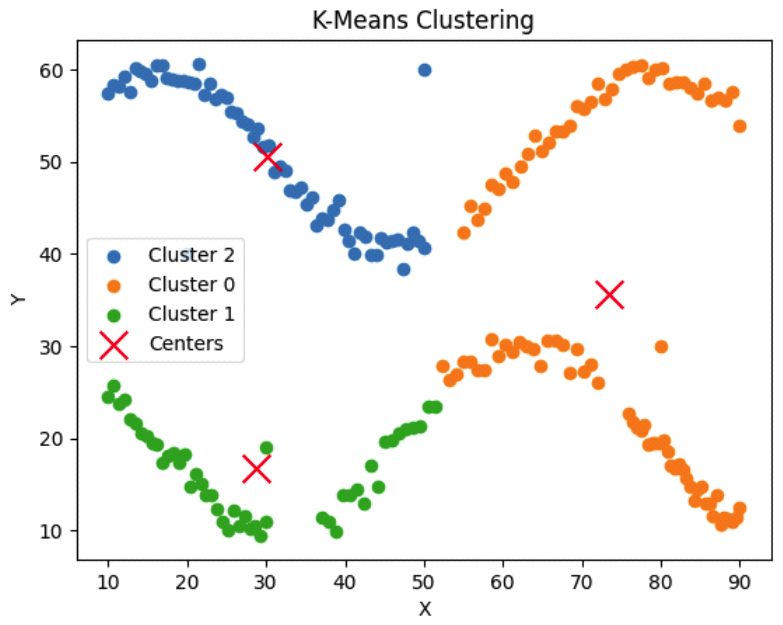
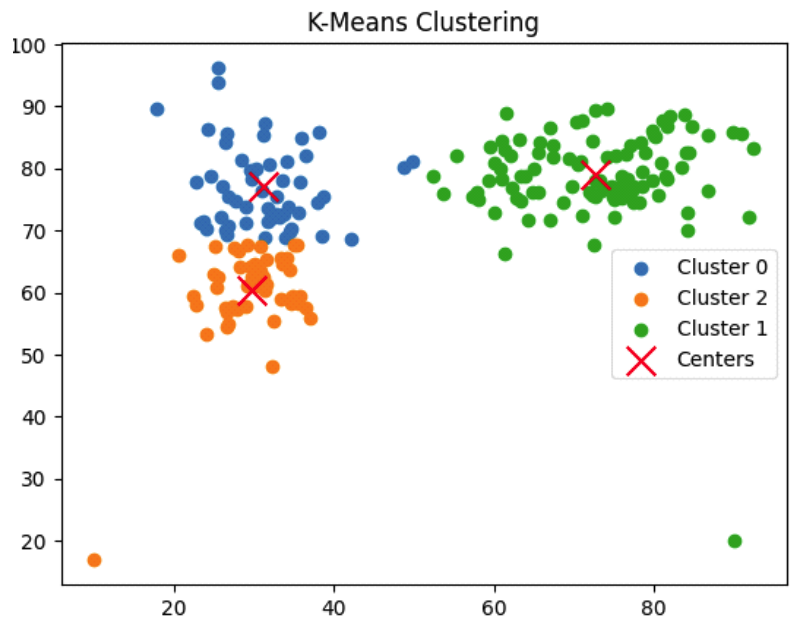
5.3 시나리오 2 : 2개의 곡선 배치두 번째 시나리오는 그림 1의(b)에서 보는 바와 같이 임무지점들이 2개의 곡선을 형성하는 경우이다. 이상치 데이터의 처리 능력을 확인하기 위해 인위적으로 이상치 데이터를 추가하였다. 그림 4는 제안하는 기법이 적용되었을 때 단계별 클러스터링 상태를 나타낸다. 한편, 그림 5는 동일한 조건에서 k-means 알고리즘을 적용했을 때의 임무할당 결과이고, 표 2는 제안하는 기법과 k-means 알고리즘을 적용했을 때 각각의 무인체계별 순회거리와 FI를 나타낸다. 두 번째 시나리오에서 무인체계의 전체 순회거리는 두 기법이 유사하다. 하지만 제안하는 기법이 k-means 알고리즘에 비해 형평성 지표가 높다. 표 2. 무인체계들의 순회거리 및 형평성 지표 (시나리오 2)
5.4 시나리오 3 : 이상치를 포함한 배치세 번째 시나리오는 그림 1의 (c)에서 보는 바와 같이 임무지점들이 2개의 군집을 형성하는 경우이다. 군집을 형성하는 임무지점들의 위치는 정규분포를 따른다. 그리고 이상치 데이터의 처리 능력을 확인하기 위해 인위적으로 이상치 데이터를 좌측과 우측 하단에 추가하였다. 그림 6은 제안하는 기법을 적용하였을 때 단계별로 임무지점들이 클러스터링되는 상태를 나타낸다. 한편, 그림 7은 동일한 조건에서 k-means 알고리즘을 적용했을 때 임무지점들의 클러스터링 결과이다. 표 3은 제안하는 기법과 k-means 알고리즘을 각각 적용했을 때 무인체계별 순회거리와 FI를 나타낸다. 세 번째 시나리오에서 무인체계의 전체 순회거리는 두 기법이 유사하다. 하지만 제안하는 기법이 k-means 알고리즘에 비해 FI가 크다. 표 3. 무인체계들의 순회거리 및 형평성 지표 (시나리오 3)
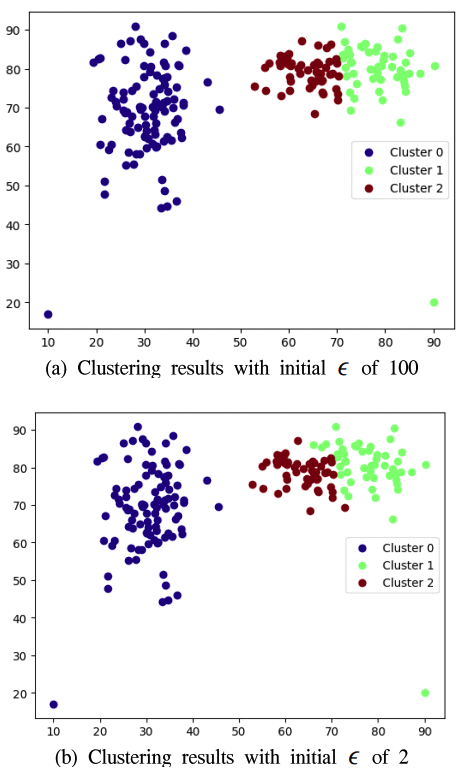
과 minPts의 영향밀도 기반의 DBSCAN 알고리즘에서 과 minPts는 클러스터링 결과에 큰 영향을 미친다. 이 크거나 minPts이 작으면 클러스터의 수가 적어지고, 이 작거나 minPts이 크면 클러스터의 수가 많아진다. 따라서, 밀도 기반의 클러스터링에서는 적절한 과 minPts를 선택하는 것이 중요하다. 하지만 제안하는 기법은 과 minPts 선정이 크게 중요하지 않다. 왜냐하면 1단계를 수행했을 때 클러스터의 개수가 적으면 제안하는 기법에서는 을 감소시키거나 minPts을 증가시키고, 클러스터의 개수가 너무 많으면 을 증가시키거나 minPts을 감소시켜 적절한 과 minPts로 수렴되기 때문이다. 그림 8은 제안한 기법에서 을 매우 큰 값(=100)으로 설정했을 때의 클러스터링 결과와 을 매우 작은 값(=2)으로 설정했을 때의 클러스터링 결과를 나타낸다. 이때, minPts는 동일하게 10으로 설정하였다. 표 4에서 보는 바와 같이 을 크게 설정한 경우와 작게 설정한 경우의 결과 차이가 크지 않다. 제안하는 기법은 초기에 부적절한 을 선택했다 하더라도 클러스터의 개수에 따라 이 적절히 갱신된다. 결과적으로 제안하는 기법에서는 과 minPts에 따른 성능 영향이 크지 않기 때문에 과 minPts를 쉽게 선택할 수 있다. 한편, 제안하는 기법에서 DBSCAN, k-means 등의 반복 횟수는 임무지점의 분포 형태, 무인체계의 수 그리고 초기 파라미터 값 등에 의해서 가변적이다. 본 실험에서의 반복 횟수는 모든 시나리오에서 3회 이하였다. Ⅵ. 결 론다수의 임무지점들을 다수의 무인체계들이 효과적으로 순회하는 것을 보장하기 위한 클러스터 기반의 임무할당 기법을 제안하였다. 제안하는 기법은 다수의 임무지점을 밀도 기반 클러스터링 기법인 DBSCAN으로 1차 클러스터링하고 클러스터의 개수와 가용 무인체계의 수를 고려하여 클러스터를 추가적으로 결합 또는 분할한다. 그리고 클러스터링 과정에서 노이즈로 처리된 임무지점을 가장 가까운 클러스터로 할당한다. 제안하는 기법을 다양한 유형의 시나리오 환경에서 실험한 결과 k-means 기반의 임무할당 기법에 비해 무인체계들의 총 순회시간을 단축한다. 뿐만 아니라 순회시간 측면에서 무인체계들에게 임무지점들을 균형되게 할당하는 것을 확인하였다. BiographyBiographyReferences
|
StatisticsCite this articleIEEE StyleJ. Lee and M. Lee, "Task Allocation Scheme for Unmanned Systems Using Density-Based Clustering in Tactical Mission Environments," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 9, pp. 1447-1456, 2025. DOI: 10.7840/kics.2025.50.9.1447.
ACM Style Jongkwan Lee and Minwoo Lee. 2025. Task Allocation Scheme for Unmanned Systems Using Density-Based Clustering in Tactical Mission Environments. The Journal of Korean Institute of Communications and Information Sciences, 50, 9, (2025), 1447-1456. DOI: 10.7840/kics.2025.50.9.1447.
KICS Style Jongkwan Lee and Minwoo Lee, "Task Allocation Scheme for Unmanned Systems Using Density-Based Clustering in Tactical Mission Environments," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 9, pp. 1447-1456, 9. 2025. (https://doi.org/10.7840/kics.2025.50.9.1447)
|