Design of Low PAPR OTSM Modulation Scheme Based on Walsh-Hadamard Transform and Random Interleaving

Ⅰ. 서 론

자율주행과 차량 간 통신 (vehicle to everything, V2X), 사물인터넷 (internet of things, IoT), 항공기 및 고속 철도와 같은 다양한 분야에서 고속 이동 통신에 대한 요구가 꾸준히 높아지고 있다. 그러나 이러한 고속 이동 통신 환경에서는 전송 채널이 시간과 주파수 축에서 빠르게 변동하므로, 안정적인 성능과 높은 효율성을 동시에 제공할 수 있는 새로운 변조 및 전송 방식이 필수적이다.

이러한 요구 사항을 충족하기 위해 제안된 OTFS 기법은 주파수-시간 (Frequency-Time, FT) 도메인에서의 다이버시티를 효과적으로 활용하여, 고속 이동 통신 환경에서도 견고한 전송 성능을 유지한다^[1,2]. 더 나아가 OTFS의 개념을 변형한 OTSM은 주파수 대신 시퀀시(sequency) 도메인에서 WHT (Walsh-Hadamard Transform)을 적용하여 다이버시티를 확보하고 실수 연산 기반 구현 방식을 채택함으로써 복잡성을 줄이면서도 OTFS와 유사한 성능을 확보할 수 있다^[3].

그러나 OTFS와 OTSM 모두 높은 첨두전압비 문제에 직면해있으며, 이는 전력 증폭기에서 비선형 왜곡을 일으켜 전력 효율과 비트 오류율 (BER) 성능을 저하시킨다^[4-6]. 이를 해결하기 위한 대안으로 DFT-s-OTFS 기법이 제안되었는데, 도플러 축에서의 DFT 사전 코딩을 통해 부가적인 정보 없이도 PAPR을 줄일 수있으나^[7], 시간 다이버시티 성능을 희생하여 고속 이동 통신 환경에서 비트 오류율 성능이 저하되는 단점이 있다.

이러한 한계를 보완하기 위해 본 논문에서는 DFT-s-OTFS 방식을 OTSM에 확장 적용한 WHT-s-OTSM (WHT-spread-OTSM)을 제안한다. WHT-s-OTSM는 도플러 축 대신 시퀀시 축에서 WHT 사전 코딩을 수행하여 첨두전압비 저감과 동시에 균일한 크기로 신호를 확산하여 다이버시티 성능을 유지할 수 있다.

또한, WHT-s-OTSM 구조를 기반으로 일반화된 기법인 SWRI-OTSM (Small WHT and Random Interleaving OTSM)을 제안한다. SWRI-OTSM은 소규 WHT와 인터리빙만으로 구현하여 WHT-s-OTSM의 구현복잡도를 낮추면서도 동등한 성능 수준을 달성하도록 설계되었다. 구체적으로 데이터 심볼 행렬을 시퀀시 축에서 서브블록 단위로 나눈 뒤 각 서브블록에 소규모 WHT를 적용하여 시간 축으로 변환함으로써 첨두전압비를 낮춘다. 그리고 시간 축으로 열 단위 랜덤 인터리빙을 수행함으로써 OTSM에 비해 줄어든 시간 다이버시티 성능을 보상한다. 그 결과, SWRI-OTSM은 부가적인 정보 없이도 첨두전압비를 효과적으로 저감하고, 고속 이동 통신 환경에서 비트 오류율 성능을 개선하며 실수 기반 연산으로 계산 복잡도를 감소시킬 수 있다.

본 논문은 WHT의 고유 특성을 활용한 새로운 OTSM 설계와 그 성능 분석을 통해 고속 이동 통신 환경에서의 실용적 적용 가능성을 제시한다. 또한, 다양한 변조 방식에서 첨두전압비 저감과 향상된 비트 오류율 성능을 보인다. 나머지 논문의 구성은 다음과 같다. II장에서는 시스템 모델을 설명하고, III장에서는 제안된 방식의 첨두전압비 및 시간 다이버시티 특성을 설명한다. IV장에서는 시뮬레이션 결과를 제시하며, 마지막으로 V장에서 결론을 정리한다.

본 논문에서 사용된 표기는 표 1로 정리하였다.

Ⅱ. 시스템 모델

이 절에서는 세 가지 변조 방식인 DFT-s-OTFS, OTSM, 그리고 제안된 SWRI-OTSM의 시스템 모델을 설명한다. 모든 시스템은 (M+Z)×N 크기의 데이터 행렬 X를 정보 심볼을 배치하는 M×N 크기의 데이터 영역과 0을 배치하는 Z×N 크기의 제로 패딩 (Zero Padding, ZP) 영역으로 구분한다. ZP 영역은 X의 마지막Z행으로 구성되며 시간 도메인에서 채널 지연 확산으로 인한 간섭을 방지하기 위해 0으로 설정된다^[8].

2.1 DFT-s-OTFS

DFT-s-OTFS 송신기에서는 첨두전압비를 줄이기 위해, (M+Z)×N 크기의 데이터 심볼 행렬 X의 각 행을 S개의 서브블록으로 나누고L(=N/S) 길이의 각 서브블록에 대하여 아래와 같이 L-point DFT를 수행한다^[7].

여기서 m = 0, 1, …, M+Z-1, k = 0, 1, …, L-1, i = 0, 1, …, S-1, 이다. [TeX:] $$\mathrm{X}_{\mathrm{DD}}$$는 지연-도플러 (Delay-Doppler, DD) 도메인에서 (M+Z)×L 크기의 서브블록들을 행 방향으로 연결한 (M+Z)×N 크기의 DD 도메인 행렬이 된다. 다음으로 아래 수식처럼, 기존 OTFS와 동일하게 XDD의 도플러 축으로N-point IDFT를 수행하여 지연- 시간 (Delay-Time, DT) 도메인 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$로 변환한다.

여기서n = 0, 1, …, N-1이다. 변환된 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$를 열 방향으로 벡터화하여 (M+Z)N×1 크기의 시간 도메인 샘플 s를 생성한다.

이후, 시간 영역 신호s는 펄스 성형 및 디지털-아날로그 컨버터 (DAC)를 거쳐 연속 시간 신호s(t)로 변환된다. s(t)는 이중 확산 채널과 AWGN 채널을 통과하여 수신 신호 r(t)가 된다. r(t)는 아날로그-디지털 컨버터(ADC)를 통해 (M+Z)N×1 크기의 수신 신호 샘플 r로 변환되고 다음의 과정을 통해 (M+Z)N 크기의 DT 도메인 신호 행렬 [TeX:] $$\mathrm{Y}_{\mathrm{DT}}$$

다음으로 [TeX:] $$\mathrm{Y}_{\mathrm{DT}}$$를 channel equalizer에 통과시켜 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$의 추정값 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DT}}$$를 얻는다. 그리고 수신 신호 행렬 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DT}}$$의 시간 축으로 N-point DFT를 수행하여 DD 도메인 행렬 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DD}}$$로 변환한다.

마지막으로 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DD}}$$의 각 서브블록마다 도플러 축으로 L-point IDFT를 적용하여 정보 심볼 추정 행렬 [TeX:] $$\widehat{\mathbf{X}}$$을 얻는다.

2.2 OTSM

OTSM 송신기는 (M+Z)×N인 지연-시퀀시(Delay-Sequency, DS) 도메인 행렬 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DS}}$$에 정보 심볼을 배치한다^[2]. 그리고 [TeX:] $$\mathrm{X}_{\mathrm{DS}}$$의 시퀀시 축을 따라 N-point WHT를 적용하여 DT 도메인의 신호 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$

이렇게 얻어진 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$를 열 방향으로 벡터화하면 아래와 같이 (M+Z)×N×1 크기의 시간 도메인 샘플 s가 된다.

수신기에서는 DFT-s-OTFS와 동일한 과정을 거쳐 DT 도메인에서 추정된 신호 행렬 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DT}}$$를 얻는다. 마지막으로 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DT}}$$의 각 행에 대해 N-point WHT 수행하여 DS 도메인에서 추정된 정보 심볼 행렬 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DS}}$$를 얻는다

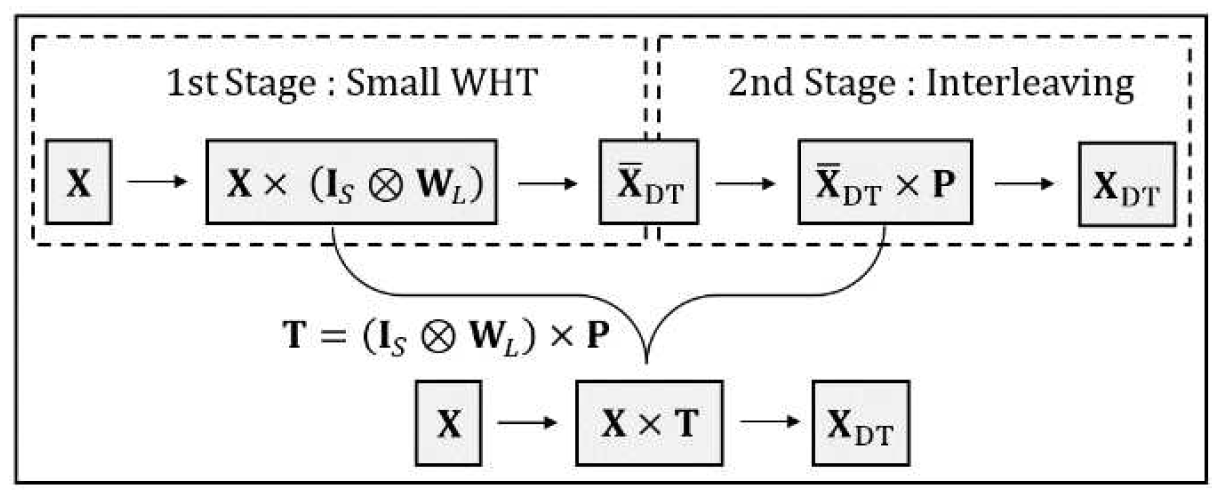
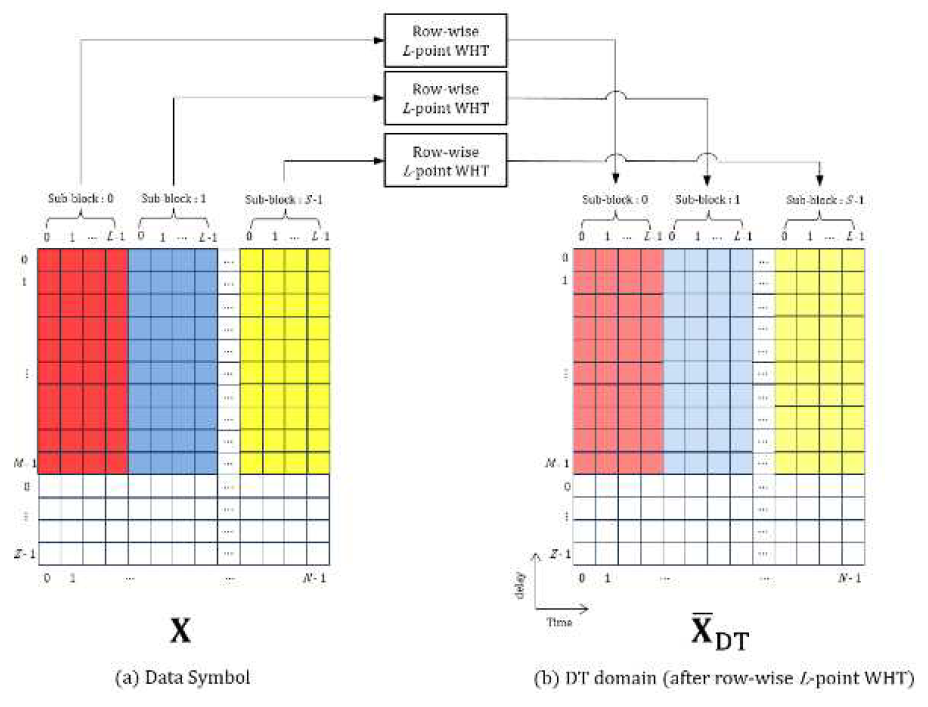
2.3 제안된 SWRI-OTSM

제안된 SWRI-OTSM 송신기는 그림 1과 같이 1st stage와 2nd stage를 통해 데이터 심볼 행렬 X를 DT 도메인의 신호 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$로 변환한다. 각 stage는 행렬 연산을 이용해 표현할 수 있고 행렬의 곱을 이용해 하나의 변환 행렬 T로 표현할 수 있다.

2.3.1 Small WHT

1st stage는 Small WHT 단계로 그림 2와 같이 (M+Z)×N 크기의 데이터 심볼 행렬 X의 행을 S개의 서브블록으로 나누고 L(= N/S)길이의 각 서브블록에 L-point WHT를 적용하여 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$를 생성한다. 이 과정은 아래의 수식과 같이 [TeX:] $$\mathrm{I}_S \text { 와 } \mathrm{W}_L$$의 크로네커곱 형태로 표현할 수 있다.

여기서 [TeX:] $$\mathrm{I}_S$$ S×S 크기의 단위 행렬이다. 이 과정은 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$의 샘플 생성 과정에서 하나의 시간 샘플에 중첩되는 X의 샘플 수를 N개에서 L개로 OTSM 보다 줄여 높은 피크 전력의 발생 가능성을 낮출 수 있다. 중첩되는 샘플 수가 많을수록 동일한 시점에서 합성되는 신호가 많아져 순간적으로 매우 큰 진폭이 발생할 확률이 높아지므로 중첩되는 샘플 수를 줄이면 시간 영역에서 신호들이 겹치는 현상이 완화되어 큰 피크가 발생할 확률이 낮아진다.

식 (7)에 따라 OTSM은 [TeX:] $$\mathrm{W}_N$$을 통해 [TeX:] $$\mathrm{X}_{DS}$$에 배치된 데이터 심볼을 N 길이의 전체 시간 슬롯에 분산시켜 높은 시간 다이버시티 성능을 얻는다. 반면, 제안된 방식은 식 (10)의 [TeX:] $$\mathrm{W}_L$$에 의해 X의 데이터 심볼이 L개의 시간 슬롯에만 분산되므로 전체 시간 도메인에서 얻을 수 있는 다이버시티 성능이 OTSM에 비해 상대적으로 감소한다. 이로 인해 도플러 효과로 인한 시간 도메인 페이딩의 영향이 심화될 수 있다. 따라서 각 서브블록 내에서L개로 분산된 신호 성분들은 시간 도메인 전체에 최대한 균등하게 분포되어야 하며 이를 위해 데이터 인터리빙이 필요하다. 인터리빙 과정은 다음과 같이 데이터 인터리빙 행렬 P를 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$에 적용하여 수행한다.

또한, SWRI-OTSM은 이 인터리빙 행렬에 무작위성을 도입하여 일반화된 변환 행렬 T를 생성한다. 따라서 P를 설계할 때는 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$의 동일한 서브블록에 속한 열들이 시간 도메인 전체에서 무작위성을 가지면서도 등간격을 유지하도록 설계해야 한다. P의 인터리빙 동작은 아래의 (1)-(3) 단계를 거쳐 등간격 열 인덱스 그룹 [TeX:] $$\mathbf{g}, \mathbf{g}^{\prime}, \mathbf{g}^{{\prime}{\prime}}$$을 순차적으로 생성한 후 (4) 단계에서 최종 인덱스 그룹 [TeX:] $$\mathbf{g}^{{\prime}{\prime}}$$을 사용하여 결정한다.

(1) 등간격 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$ 생성:

전체 열 인덱스가N개 있을 때, 등간격 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$는 S간격으로 떨어진 인덱스들을 모아서 형성된다. 이는 각 서브블록이L개의 열로 구성되므로 하나의 인덱스 그룹이 L개의 원소를 가져야 하기 때문이다. 따라서 전체 N개의 인덱스 중에서 가장 멀리 떨어진 L개의 인덱스들을 선택하게 되며, 이로 인해 각 인덱스는 S간격으로 떨어지게 된다. 이렇게 형성된 총 S개의 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$는 다음과 같이 표현된다.

여기서 i는 서브블록 인덱스이며 a는 서브블록 내의 열 인덱스이다. 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$에 속한 인덱스들은 동일한 서브블록에 배정되어 서브블록 내 각 열들의 새로운 위치를 결정한다.

(2) 각 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$의 원소 무작위 재배열:

이후, 식 (12)에서 생성된 인덱스 그룹 [TeX:] $$\mathbf{g}_i$$의 원소들을 무작위로 섞어 새로운 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime}_i$$를 생성한다.

퍼뮤테이션 행렬 [TeX:] $$\Pi_{\pi_{\text {rand }, L}}$$는 L 길이의 무작위 순열 벡터 [TeX:] $$\boldsymbol{\pi}_{\text {rand }, \boldsymbol{L}}$$에 따라 [TeX:] $$\mathbf{g}_i$$의 원소들을 재배열한다.

(3) 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime}_i$$간의 순서 무작위 재배열:

마지막으로 서브블록 단위에서 인덱스 그룹을 무작위로 배정하기 위해 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime}_i$$들의 순서를 S 길이의 무작위 순열 벡터 [TeX:] $$\boldsymbol{\pi}_{\mathrm{rand}, S}$$로 무작위로 재배열하여 최종 열 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$를 생성한다.

[TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$는 S 간격으로 무작위하게 배치된 L개의 열 인덱스로 구성된 인덱스 그룹으로, i번째 서브블록에 할당된다.

(4) [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$를 이용한 열 단위 데이터 인터리빙 수행:

데이터 인터리빙 행렬 P는 최종 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$를 따라 다음과 같이 정의된다.

여기서 p, q = 0, 1, 2, …, N-1 이다. P의 p번째 행에서 [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$의 값에 해당하는 열에 1을 배치하면 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$의 p번째 열이 [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$의 값에 해당하는 열로 이동하게 된다. 그림 3은 인덱스 그룹 [TeX:] $$\mathbf{g}^{\prime \prime}{ }_i$$에 의해 [TeX:] $$\overline{\mathbf{X}}_{\mathrm{DT}}$$의 i번 서브블록의 열들을 재배열하여 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$로 변환하는 예시이다.

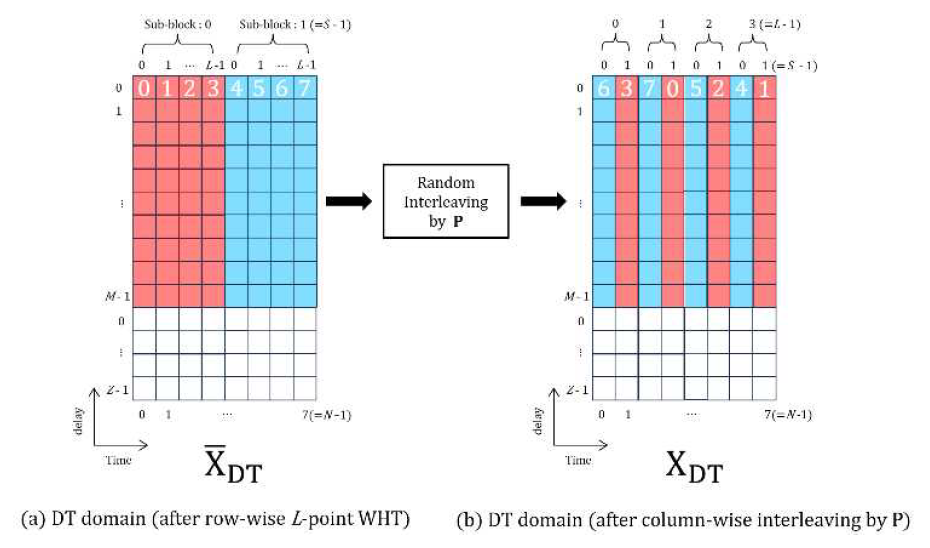지금까지 설명한 1st stage와 2nd stage의 변환과정은 각각 행렬 연산으로 표현할 수 있으며 두 과정을 하나의 변환 행렬 T로 표현하면 다음과 같다.

(M+Z)×N 크기의 데이터 심볼 행렬 X에 T를 적용하면 SWRI-OTSM 변조된 DT 도메인의 신호 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$를 생성할 수 있다.

식 (17)의 결과로 얻어진 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$는 식 (3)-(4)에서 설명된 단계를 동일하게 따른다. (M+Z)N×1 크기의 시간 도메인 샘플 벡터 s로 변환한 후, s를 사용하여 DT 도메인 수신 신호 행렬 [TeX:] $$\mathrm{Y}_{\mathrm{DT}}$$를 생성한다. 수신기에서는 [TeX:] $$\mathrm{Y}_{\mathrm{DT}}$$를 channel equalizer에 통과시켜 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$의 추정값인 [TeX:] $$\widehat{\mathbf{X}}_{\mathrm{DT}}$$를 생성한다. 마지막으로 SWRI-OTSM의 역변환 행렬 [TeX:] $$\mathbf{T}^{-1} \text { 를 } \widehat{\mathbf{X}}_{\mathrm{DT}}$$에 적용하면 복조된 데이터 심볼 추정 행렬 [TeX:] $$\widehat{\mathbf{X}}$$를 얻을 수 있다.

Ⅲ. 제안된 SWRI-OTSM의 변환 행렬 특성

SWRI-OTSM에서는 변환 행렬 T의 구조적 특성이 DT 도메인에서 첨두전압비 감소와 시간 다이버시티 성능에 중요한 역할을 한다. 그림 4에서 나타나 있듯이 T는 식 (17)에 따라 모든 행과 열에 0이 아닌 원소가 L개씩 포함되도록 구성된다. 본 절에서는 이러한 구조가 첨두전압비를 낮추는 원리를 살펴보고 이어서 시간 다이버시티 성능을 어떻게 제공하는지 설명한다.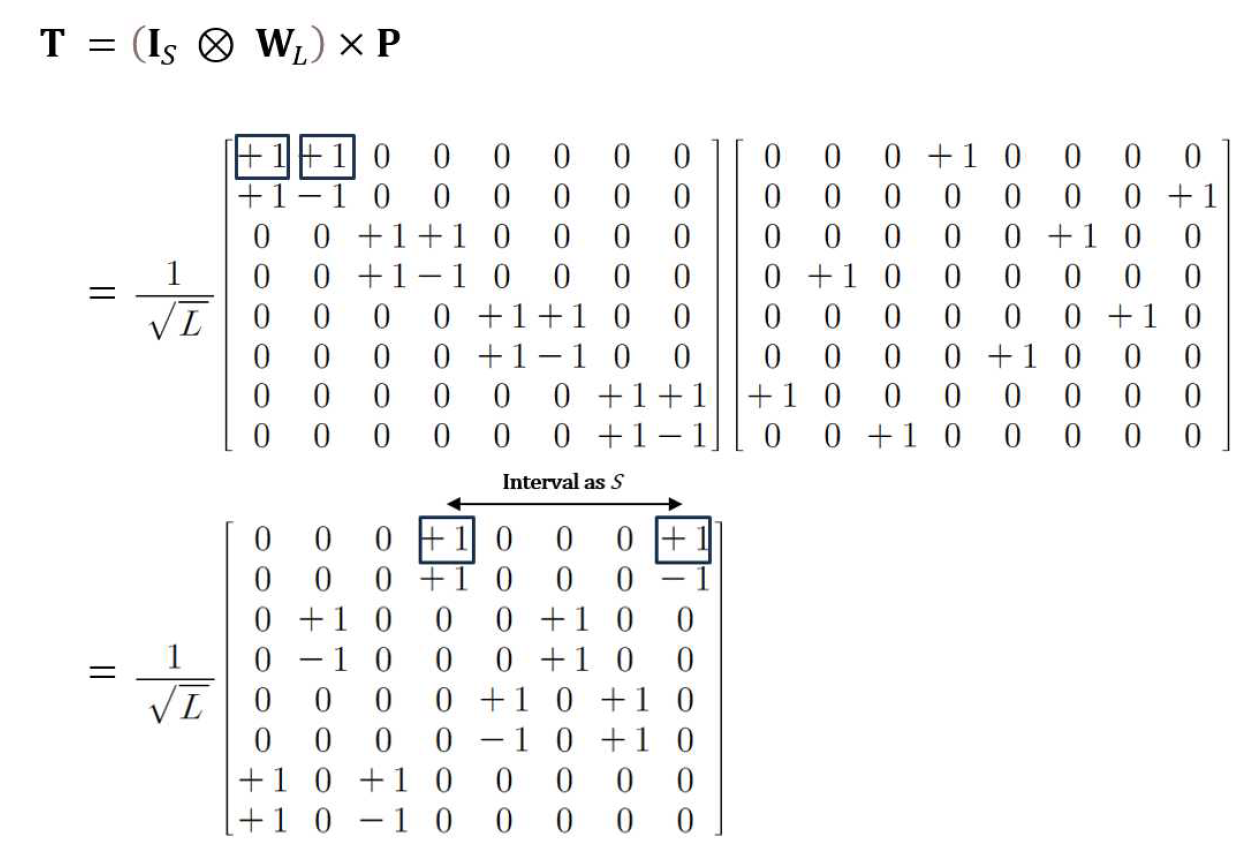

3.1 첨두전압비 특성

OTSM에서는 식 (7)과 같이N-point WHT를 통해 [TeX:] $$\mathrm{X}_{\mathrm{DS}} \text { 가 } \mathrm{X}_{\mathrm{DT}}$$로 변환되는 과정에서 시퀀시 도메인의 모든 신호 샘플 (N개)이 동일한 시간 도메인 샘플에 중첩된다. 이때 데이터 샘플은 같은 부호로 중첩되어 더 큰 값을 형성하거나 반대 부호로 중첩되어 더 작은 값을 형성하여 신호에 변동을 일으킨다. 중첩되는 샘플의 개수가 증가할수록 이러한 변동 폭이 더 커지므로 신호의 피크 전력이 높게 형성된다. 반면에 SWRI-OTSM에서 T를 이용한 데이터 심볼의 분산은 기존 OTSM 방식과 비교했을 때 DT 도메인에서 중첩되는 신호의 개수를 줄이는 특성이 있다. 식 (18)에서 DT 도메인의 (m,n)번째 샘플 [TeX:] $$\mathrm{X}_{\mathrm{DT}}[m, n]$$은 X의 m번째 행과 T의 n번째 열의 내적을 계산하여 얻어진다. 그림 4에서 행렬 T의 각 열은 ±1로 구성된 항목이 L개, 0인 항목이 N-L개 이므로, 하나의 시간 도메인 샘플에 중첩되는 데이터 샘플의 개수가 N개에서 L개로 감소하여 OTSM 대비 더 낮은 첨두전압비를 달성한다.

N이 고정된 경우에는 L의 크기에 따라 첨두전압비의 크기가 결정된다. S가 커질수록 L이 작아지므로 하나의 시간 도메인 샘플에 중첩되는 신호의 개수가 줄어들어 첨두전압비가 낮아진다. 반대로 S가 작아지면 L이 커지므로 중첩되는 신호의 개수가 많아져 첨두전압비가 높아진다. S가 1이 되는 경우는 OTSM과 동일하게 동작한다.

3.2 시간 다이버시티 특성

시간 다이버시티는 채널이 시간 도메인에서 변화할 때 신호를 다양한 시간 슬롯에 분산하여 전송함으로써 수신 시 신호 복원력을 높이는 개념이다. T는 각 행마다 L개의 원소를 갖도록 구성되므로 X의 데이터 심볼은 시간 도메인 상에서 L개의 위치로 분산된다. 또한, 그림 4와 같이 T의 0이 아닌 원소들은 모두 ±1이므로 모든 데이터 심볼은 동일한 에너지를 유지하면서 시간 도메인에 분산된다. 그리고 II절의 2.3에서 설명한 인터리빙 연산이 적용되어 T의 각 행의 원소는 S간격으로 배치되므로 분산된 데이터 심볼들이 특정 구역에 몰리는 현상을 방지할 수 있다.

3.3 동등한 변환 행렬 구현 예시

SWRI-OTSM의 변환 행렬 T는 랜덤 인터리빙을 통해 다양한 원소의 배치를 가질 수 있다. 이때. 각 행과 열에 포함된 0이 아닌 원소의 개수가 L개로 유지되고 행에서 원소가 S간격으로 배치된다는 조건이 충족되면 이러한 무작위성에도 불구하고 구조적 특성으로 인해 동일한 첨두전압비 저감 효과와 시간 다이버시티 성능을 제공할 수 있다. T의 도메인 변환 효과를 확인하고 구조를 보다 직관적으로 이해하기 위해 T의 일부 패턴을 구현할 수 있는 예시로 WHT-s-OTSM을 제안한다.

WHT-s-OTSM은 기존의 DFT-s-OTFS 변조 과정에서 DFT와 IDFT를 WHT로 교체하여 OTSM으로 확장한 방식이다. 우선, 식 (1)에서 (M+Z)×N 크기의 데이터 심볼 행렬 X의 각 행을 [TeX:] $$S^{\prime}$$개의 서브블록으로 나누고 [TeX:] $$L^{\prime}\left(=N / S^{\prime}\right)$$ 길이의 서브블록마다 [TeX:] $$L^{\prime}$$-point WHT를 수행하여 DS 영역으로 변환한다.

[TeX:] $$m=0,1, \cdots, M+Z 1, k=0,1, \ldots L^{\prime}-1, i=0,1, \ldots, S^{\prime}-1 .$$ 식 (19)의 [TeX:] $$\mathrm{X}_{\mathrm{DS}}$$에서 시퀀시 도메인으로 N-point WHT를 적용하여 DT 도메인 행렬 [TeX:] $$\mathrm{X}_{\mathrm{DT}}$$를 생성한다.

식 (19)와 식 (20)의 과정은 행렬 연산으로 표현할 수 있고 다음과 같이 하나의 변환 행렬 [TeX:] $$\mathrm{T}_{\mathrm{Ws}}$$로 정의할 수 있다.

(M+Z)×N 크기의 데이터 심볼 행렬 X에 식 (21)을 적용하면 DT 도메인의 신호 행렬 [TeX:] $$\mathrm{T}_{\mathrm{DT}}$$를 생성할 수 있다.

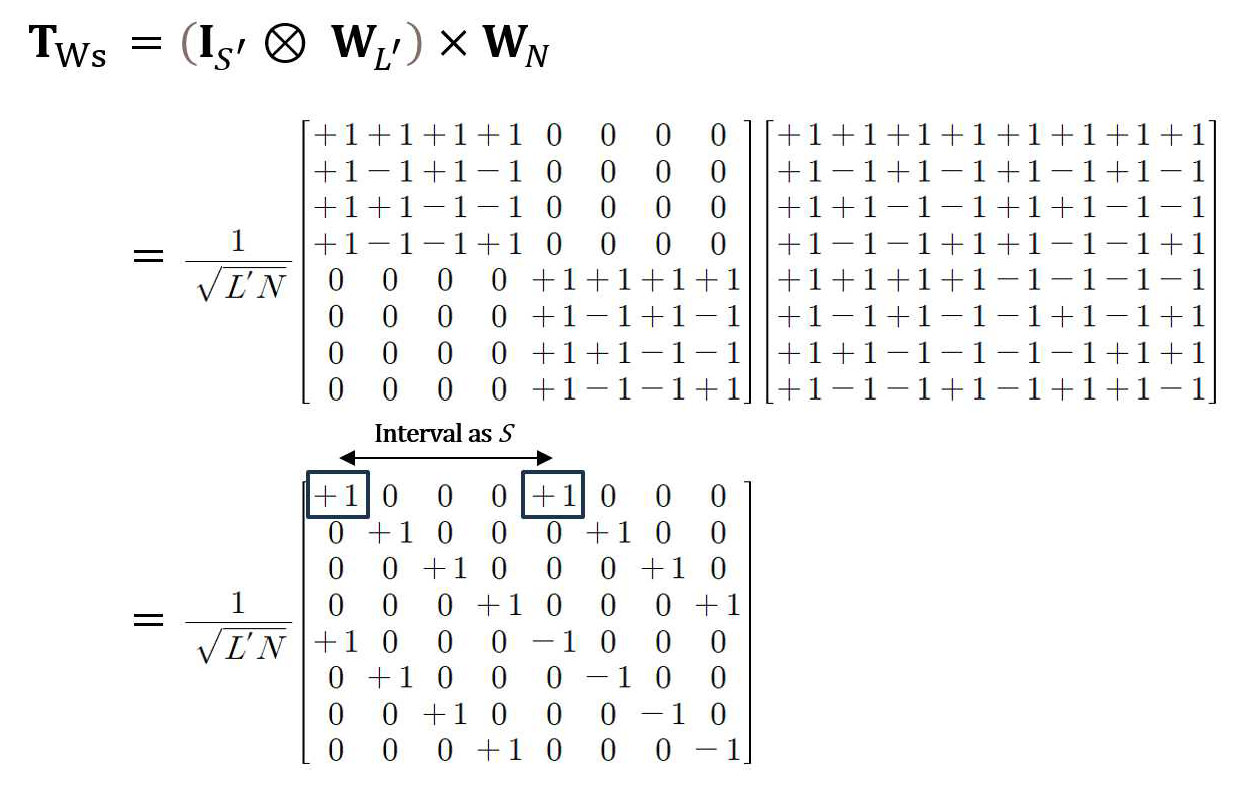그림 5를 통해 WHT-s-OTSM은 SWRI-OTSM에서 사용한 파라미터 값 S = 4와 L = 2를 서로 반대로 바꾸어 [TeX:] $$S^{\prime}, L^{\prime}$$로 설정하면 각 행과 열의 0이 아닌 원소의 개수가 SWRI-OTSM의 변환 행렬 T와 동일해짐을 확인할 수 있다. T와 [TeX:] $$\mathrm{T}_{\mathrm{W}_{\mathrm{S}}}$$는 변환행렬의 열에 존재하는 원소 개수에 의해 첨두전압비가 결정되고 행에 존재하는 원소 개수에 의해 시간 다이버시티 성능이 결정되는 구조적 특성이 동일하므로 서로 같은 성능을 제공한다.

Ⅳ. 실험 결과

이 절은 제안된 SWRI-OTSM의 성능을 비트 오류율 및 첨두전압비의 CCDF 관점에서 평가하고 기존의 DFT-s-OTFS 및 OTSM 방식과도 비교한다. carrier frequency는 4 GHz로 설정하고 송신기와 수신기 간의 채널은 Extended Vehicular A (EVA) 모델을 적용하였다. 또한, 수신기에서는 time domain block-wise LMMSE (linear minimum mean square error) equalization을 사용하였다^[8-10]. 실험에서는 N값에 따라 SWRI-OTSM 및 DFT-s-OTFS의 서브블록의 개수 S와 서브블록의 길이 L(= N/S)을 조정한다. 예를 들어, N = 16인 경우에는 SWRI-OTSM과 DFT-s-OTFS 모두 S를 1, 2, 4, 8, 16으로 설정한다면 그에 따라L-point 변환의 크기L은 각각 16, 8, 4, 2, 1을 적용한다. 이때, SWRI-OTSM은L-point WHT를, DFT-s-OTFS에서는 L-point DFT를 사용한다.

송신 신호 s(t)의 첨두전압비는 n번째 심볼 단위로 나누어 아래와 같이 계산된다.

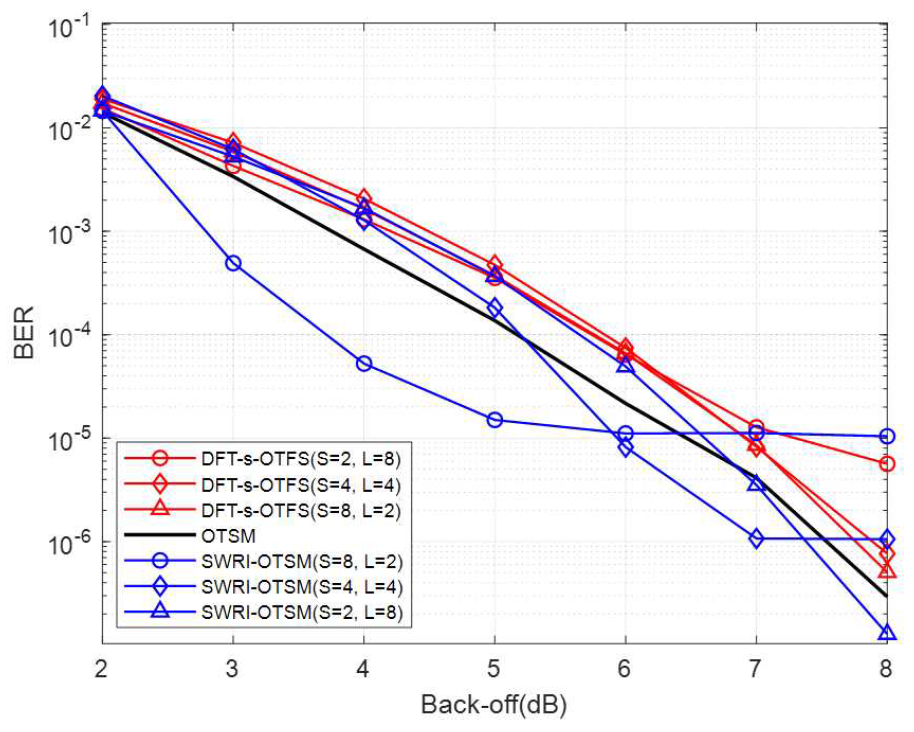
여기서 [TeX:] $$P_{\text {avg }}$$는 s(t)의 평균 전력이다. 또한, 송신 신호에 고출력 증폭기 (High Power Amplifier, HPA) 백오프 (Back-Off)를 적용하여 평균 전력 대비 설정된 클리핑 (Clipping) 기준 전력에 따라 송신 신호의 피크 전력을 제한한다.

그림 6은 QPSK 환경에서 다양한 SNR에 따른 비트 오류율 측정 결과를 나타낸 것으로, 무한 백오프 (즉, 첨두전압비로 인한 신호 왜곡 없음)를 가정한 상황이다. 이 시나리오에서는 각 방식의 다이버시티 성능이 비트 오류율 성능에 미치는 영향을 관찰할 수 있다. SWRI-OTSM와 DFT-s-OTFS는 시간 축으로 확산되는 신호의 크기 차이가 발생하면서 비트 오류율 성능 차이가 나타난다. 이는 첨두전압비 개선 효과가 없는 상황에서도 SWRI-OTSM이 DFT-s-OTFS보다 시간 채널 페이딩에 대한 신호 복원 능력을 더 높게 유지함을 의미한다.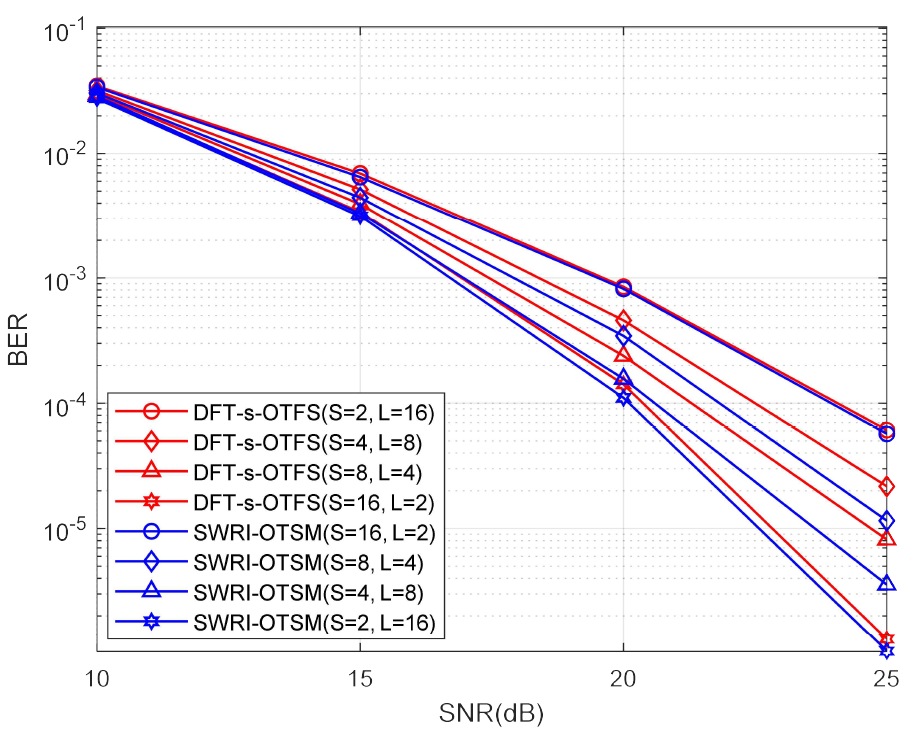

그림 7은 제안된 SWRI-OTSM과 기존 DFT-s-OTFS 및 OTSM 방식의 첨두전압비 성능을 비 교한 결과를 보여준다. 결과에 따르면 서브블록 수 S 가 증가할수록 SWRI-OTSM과 OTSM 간 첨두전압비 성능 차이가 더욱 커지는 것을 확인할 수 있다. 특히, SWRI-OTSM (S = 8, L = 2)은 CCDF(=Pr[PAPR[TeX:] $$\gt \left.\left.\mathrm{PAPR}_0\right]\right)=10^{-4}$$에서 OTSM 대비 약 7 dB 정도 낮은 첨두전압비를 보인다. 이러한 개선은 식 (10)에서 확인할 수 있듯이 DT 도메인에서 중첩되는 신호의 수를 L개로 줄인 결과이다. 한편, DFT-s-OTFS는 DFT 사전 코딩을 통해 식 (2)의N-point IDFT 효과를 일부 상쇄하여 첨두전압비를 감소시키지만 여전히 DT 도메인에서 N개의 신호가 중첩되어 SWRI-OTSM 만큼의 첨두전압비 저감 효과를 얻지 못한다.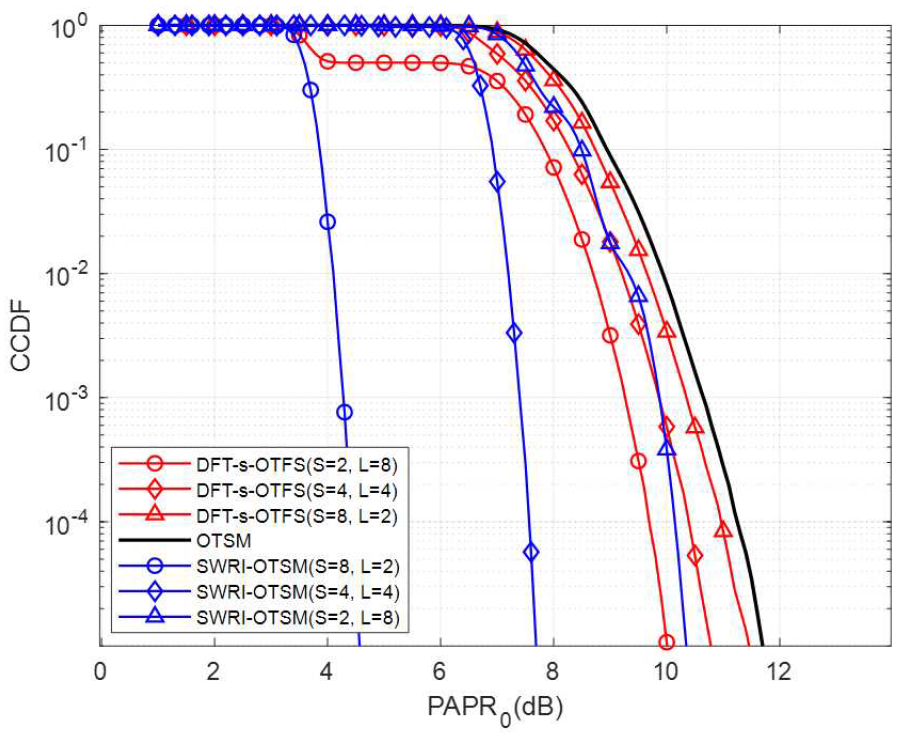

그림 8은 백오프 레벨에 따른 비트 오류율 성능을 다양한 파라미터에서 비교한 결과를 보여준다. 먼저 그림 8(a)-(c)에서 DFT-s-OTFS의 경우, 서브블록 개수 S를 줄이면 첨두전압비는 감소하지만 다이버시티 성능이 감소하여 전체적으로 비트 오류율 성능이 저하된다. 반면, SWRI-OTSM은 2-5 dB 구간에서 OTSM보다 우수한 비트 오류율 성능을 보이는데, 이는 SWRI-OTSM에서 L의 크기를 감소시킴으로써 DT 도메인에서 중첩되는 신호의 수를 줄여 첨두전압비를 크게 개선했기 때문이다. 그 결과, 백오프 레벨이 낮은 구간에서는 다른 전송 방식 대비 뛰어난 비트 오류율 성능을 확인할 수 있다. 또한, 그림 8(c)에서 DFT-s-OTFS (S = 4, L = 4)와 SWRI-OTSM (S = 2, L = 8)은 그림 7에서 유사한 첨두전압비 성능을 보임에도 불구하고, 모든 백오프 레벨에 걸쳐 SWRI-OTSM이 더 우수한 비트 오류율 성능을 나타낸다.

그림 8(a)와 (b)에서는 백오프가 약 5 dB일 때, SWRI-OTSM 중L = 2인 경우가L이 큰 다른 설정보다 더 우수한 비트 오류율 성능을 보인다. 그림 8(c)에서는 백오프가 약 6 dB일 때 유사한 성능 역전 현상이 관찰된다. 이는 백오프가 충분하지 않은 상황에서는 첨두전압비를 낮추는 방향으로 설계한 SWRI-OTSM이 유리하지만, 백오프가 충분히 큰 상황에서는L 값을 더 크게 설정하여 시간 다이버시티 성능을 확보하는 편이 비트 오류율 성능 면에서 유리해지는 것을 보여준다. 결과적으로, 백오프 환경이 어떻게 주어지느냐에 따라 L의 크기를 조정함으로써 첨두전압비 저감과 시간 다이버시티 이득 사이의 최적의 비트오류율 성능을 얻을 수 있다.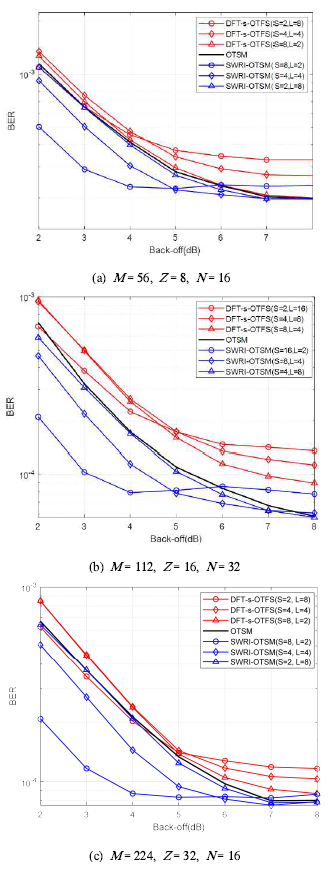

그림 9는 16-QAM 환경에서 각 변조 방식의 첨두전압비 특성을 비교한 결과를 보여준다. 16-QAM에서도 SWRI-OTSM은 S가 증가할수록 첨두전압비가 낮아지고, DFT-s-OTFS는 S가 감소할수록 첨두전압비가 낮아지는 경향을 보인다. CCDF가 10^-4일 때, SWRI-OTSM(S = 8, L = 2)은 OTSM 비해 약 4 dB, DFT-s-OTFS(S = 2, L = 8)에 비해 3 dB 개선된 첨두전압비 성능을 제공한다.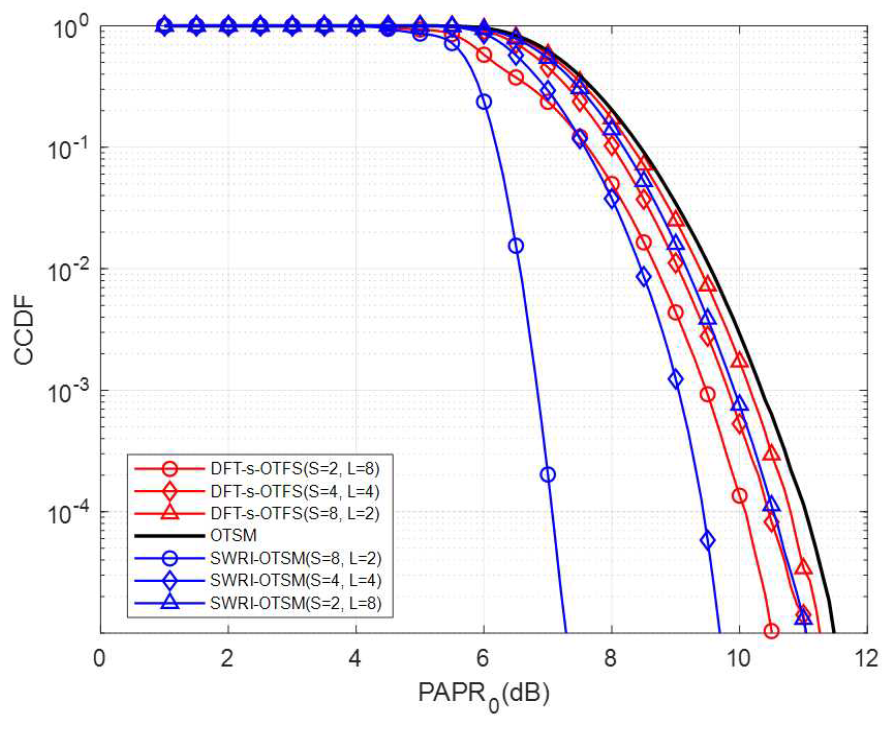

그림 10은 백오프 레벨 변화에 따른 비트 오류율 성능을 비교한 결과를 나타낸다. 먼저, SWRI-OTSM (S = 8, L = 2)은 백오프 레벨이 약 3~6 dB 정도의 낮은 구간에서 OTSM 및 DFT-s-OTFS보다 우수한 비트 오류율 성능을 보이며, 특히 4-5 dB 부근에서 그 격차가 가장 크게 나타난다. 반면, 백오프 레벨이 충분히 커서 클리핑이 발생하지 않는 구간(그림 13에서 백오프 7.5 dB 이상)에서는 다이버시티 효과를 최대화한 경우, 즉, SWRI-OTSM의 (S = 1)인 경우(기존 OTSM과 동일)일 때 가장 높은 비트 오류율 성능을 달성한다. 결국 백오프 레벨이 달라지는 실제 상황에서는 SWRI-OTSM의 (S, L) 파라미터를 동적으로 조정함으로써 최적의 비트 오류율 성능을 얻을 수 있다. 예를 들어, 백오프가 충분치 않은 경우에는(S= 8 또는 4)와 적절한 L을 선택하여 첨두전압비 저감 효과를 극대화하고, 백오프 여유가 큰 경우에는 (S = 1)로 설정하여 최대 다이버시티 효과를 확보하는 식이다. 이로써 SWRI-OTSM은 다양한 채널 상태 및 시스템 제약에 탄력적으로 대응하면서, 클리핑에 따른 비트 오류율 저하를 최소화하고 안정적인 전송 품질을 유지할 수 있다.

Ⅴ. 결 론

본 논문에서는 기존 DFT-s-OTFS와 OTSM이 가진 한계를 극복하기 위해 새로운 변조 방식인 SWRI-OTSM을 제안하였다. 제안된 SWRI-OTSM은 별도의 부가정보 없이도 첨두전압비를 효과적으로 낮추면서 시간 다이버시티 성능을 일부 유지하여 고속 이동 환경에서도 우수한 비트 오류율 성능을 제공한다. SWRI-OTSM은L-point WHT와 열 단위 인터리빙 과정을 통해 DT 도메인에서 OTSM에 발생하는 피크 전력 문제를 완화한다. 또한, 서브블록 분할로 인해 감소된 시간 다이버시티 성능을 열 단위 인터리빙을 통해 보완함으로써 시간 채널 페이딩에 대한 높은 복원력을 유지한다. 시뮬레이션 결과, SWRI-OTSM은 DFT-s-OTFS와 OTSM에 비해 첨두전압비를 감소시키고 낮은 백오프 환경에서 우수한 비트 오류율 성능을 보였다. 아울러, 제안된 SWRI-OTSM은 WHT의 특성을 활용하여 실수 기반 연산으로 낮은 계산 복잡도를 가지면서 동일한 성능을 제공하는 일반적인 버전을 제시하였다.